- 2021-04-17 发布 |
- 37.5 KB |
- 13页

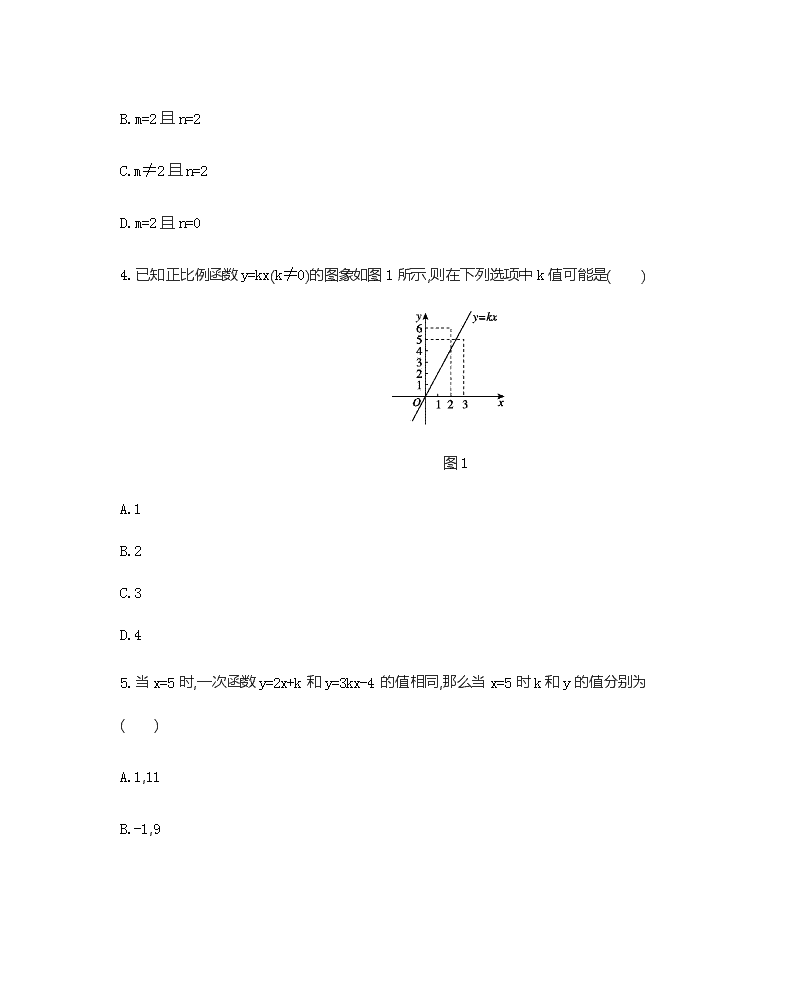

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版八年级数学(下册)第十九章测试卷(附答案)
人教版八年级数学(下册) 第十九章测试卷 1.下列y关于x的函数中,是正比例函数的为( ) A.y=x2 B.y= C.y= D.y= 2.已知直线y=x+b,当b<0时,直线不经过( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.函数y=(m-2)xn-1+n是一次函数,m,n应满足的条件是( ) A.m≠2且n=0 B.m=2且n=2 C.m≠2且n=2 D.m=2且n=0 4.已知正比例函数y=kx(k≠0)的图象如图1所示,则在下列选项中k值可能是( ) 图1 A.1 B.2 C.3 D.4 5.当x=5时,一次函数y=2x+k和y=3kx-4的值相同,那么当x=5时k和y的值分别为( ) A.1,11 B.-1,9 C.5,11 D.3,3 6.已知点M(1,a)和点N(2,b)是一次函数y=-2x+1图象上的两点,则a与b的大小关系是( ) A.a>b B.a=b C.anx+4n>0的整数解为( ) 图3 A.-1 B.-5 C.-4 D.-3 10.小亮家与姥姥家相距24 km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程s(km)与北京时间t(时间)的函数图象如图4所示.根据图象得到结论,其中错误的是( ) 图4 A.小亮骑自行车的平均速度是12 km/h B.妈妈比小亮提前0.5小时到达姥姥家 C.妈妈在距家12 km处追上小亮 D.9:30妈妈追上小亮 11.已知一次函数图象经过点(-1,2)且y随x的增大而减小,请写出一个满足上述条件的函数关系式: . 12.一次函数y=2x+3与y=3x-2b的图象交x轴于同一点,则b= . 13.将直线y=3x+2沿y轴向下平移5个单位长度,则平移后直线与y轴的交点坐标为 . 14.经过点(2,0)且与坐标轴围成的三角形的面积为2的直线的表达式是 . 15.如图5所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省 元. 图5 16.正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图6所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=x+1和x轴上,已知点B1(1,1),B2(3,2),则B5的坐标是 . 图6 17.已知一次函数y=kx+b的图象经过M(0,2),N(1,3)两点. (1)求k,b的值; (2)若一次函数y=kx+b的图象与x轴的交点为A(a,0),求a的值. 18.若直线y=kx+6与两坐标轴所围成的三角形面积是24,求常数k的值. 19.绵州大剧院举行专场音乐会,成人票每张20元,学生票每张5元.暑假期间,为了丰富广大师生的业余文化生活,剧院制定了两种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的90%付款.某校有4名老师与若干名(不少于4人)学生听音乐会. (1)设学生人数为x(人),付款总金额为y(元),分别建立两种优惠方案中y与x的函数关系式; (2)请计算并确定出最节省费用的购票方案. 20.某工厂有甲、乙两条生产线先后投产,在乙生产线投产以前,甲生产线已生产了200 t成品;从乙生产线投产开始,甲、乙两条生产线每天生产20 t和30 t. (1)分别求出甲、乙两条生产线投产后,甲、乙的生产总量y甲(t)和y乙(t)与从乙开始投产以来所用的时间x(天)之间的函数关系式,并指出第几天结束时,甲、乙两条生产线的总产量相同; (2)在平面直角坐标系中,作出上述两个函数在第一象限内的图象,观察图象分别指出第15天和第25天结束时,哪条生产线的总产量高. 21.(14分)为加强公民的节水意识,合理利用水资源,某市对居民用水实行阶梯水价.居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于1∶1.5∶2.如图7所示的折线表示实行阶梯水价后每月水费y(元)与用水量x (m3)之间的函数关系.其中线段AB表示第二级阶梯时y与x之间的函数关系. (1)写出点B的实际意义; (2)求线段AB所在直线的表达式; (3)某户5月份按照阶梯水价应缴水费102元,其相应用水量为多少立方米? 图7 参考答案 1.C 2.B 3.C 4.B 5.A 6.A 7.D 8.C 9.D 10.D 11.y=-x+1(答案不唯一) 12. 13.(0,3) 14. y=x-2或y=-x+2 15.2 16.(31,16) 17.解:(1) 因为y=kx+b的图象过M(0,2),N(1,3)两点,所以解得 (2) 由(1)知,k=1,b=2,所以y=x+2,又因为其图象与x轴交于点A(a,0), 所以0=a+2,a=-2. 18. 解:设直线y=kx+6与x轴和y轴分别交于点A,B. 令y=0得x=-;令x=0得y=6.所以A,B(0,6). 所以OA=,OB=|6|=6. 所以S=OA·OB=×6=24. 所以|k|=,所以k=±. 19.解:(1)按优惠方案1可得y1=20×4+(x-4)×5=5x+60(x≥4), 按优惠方案2可得y2=(5x+20×4)×90%=4.5x+72(x≥4). (2) 因为y1-y2=0.5x-12(x≥4), ①当y1-y2=0时,得0.5x-12=0,解得x=24, ∴当学生人数为24时,两种优惠方案付款一样多. ②当y1-y2<0时,得0.5x-12<0,解得x<24, ∴当4≤x<24时,y1查看更多