- 2021-04-17 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020高中数学 第三章 空间向量与立体几何阶段复习课学案 新人教A版选修2-1
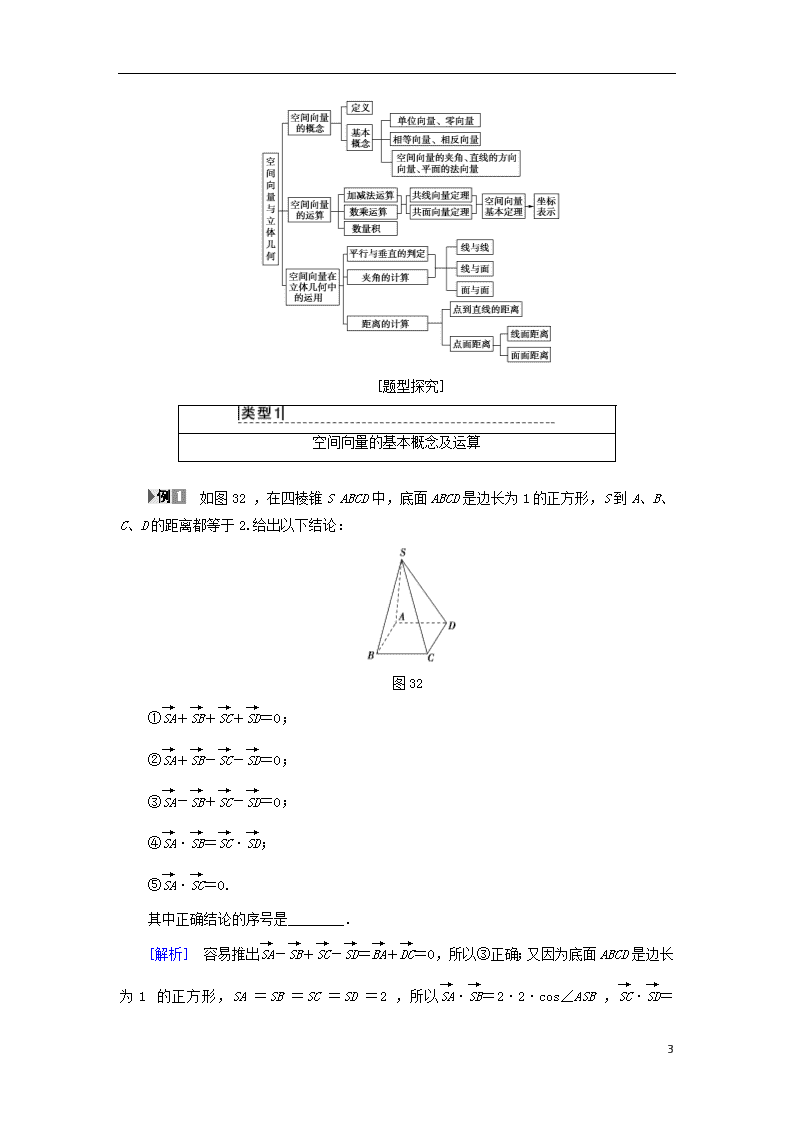
第三课 空间向量与立体几何 [核心速填] 1.空间向量的有关定理和推论 (1)共线向量定理:对空间任意两个向量a,b(b≠0),a∥b的充要条件是存在实数λ,使得a=λb. (2)共线向量定理的推论:若,不共线,则P,A,B三点共线的充要条件是=λ+μ,且λ+μ=1. (3)共面向量定理:如果两个向量a,b不共线,那么向量p与向量a,b共面的充要条件是存在惟一的有序实数对(x,y),使得p=xa+yb. (4)共面向量定理的推论:已知空间任意一点O和不共线的三点A,B,C,则P,A,B,C四点共面的充要条件是=x+y+z(其中x+y+z=1). (5)空间向量基本定理:如果三个向量a,b,c不共面,那么对空间任一向量p,存在有序实数组{x,y,z},使得p=xa+yb+zc,其中{a,b,c}叫做空间的一个基底. 2.空间向量运算的坐标表示 设a=(a1,a2,a3),b=(b1,b2,b3). (1)a+b=(a1+b1,a2+b2,a3+b3), a-b=(a1-b1,a2-b2,a3-b3), λa=(λa1,λa2,λa3), a·b=a1b1+a2b2+a3b3. (2)重要结论: a∥b⇔a=λb⇔a1=λb1,a2=λb2,a3=λb3(λ∈R); a⊥b⇔a·b=0⇔a1b1+a2b2+a3b3=0. 3.模、夹角和距离公式 (1)设a=(a1,a2,a3),b=(b1,b2,b3),则 ①|a|==; ②cos〈a,b〉==. (2)设A(a1,b1,c1),B(a2,b2,c2),则 dAB=||=. 4.空间向量的结论与线面位置关系的对应关系 (1)设直线l的方向向量是u=(a1,b1,c1),平面α的法向量v=(a2,b2,c2), 则l∥α⇔u⊥v⇔u·v=0⇔a1a2+b1b2+c1c2=0,l⊥α⇔u∥v⇔u=kv⇔(a1,b1,c1)= 11 k(a2,b2,c2)⇔a1=ka2,b1=kb2,c1=kc2(k∈R). (2)设直线l,m的方向向量分别为a,b,平面α,β的法向量分别为u,v,则 l∥m⇔a∥b⇔a=kb,k∈R; l⊥m⇔a⊥b⇔a·b=0; l∥α⇔a⊥u⇔a·u=0; l⊥α⇔a∥u⇔a=ku,k∈R; α∥β⇔u∥v⇔u=kv,k∈R; α⊥β⇔u⊥v⇔u·v=0. 5.空间向量与空间角的关系 (1)设异面直线l1,l2的方向向量分别为m1,m2,则l1与l2的夹角θ满足cos θ=|cos〈m1,m2〉|. (2)设直线l的方向向量和平面α的法向量分别为m,n,则直线l与平面α的夹角θ满足sin θ=|cos〈m,n〉|. (3)求二面角的大小: (ⅰ)如图31①,AB,CD是二面角αlβ的两个半平面α,β内与棱l垂直的直线,则二面角的大小θ=〈,〉. 图31 (ⅱ)如图31②③,n1,n2分别是二面角αlβ的两个半平面α,β的法向量,则二面角的大小θ满足cos θ=cos〈n1,n2〉或-cos〈n1,n2〉. [体系构建] 11 [题型探究] 空间向量的基本概念及运算 如图32,在四棱锥SABCD中,底面ABCD是边长为1的正方形,S到A、B、C、D的距离都等于2.给出以下结论: 图32 ①+++=0; ②+--=0; ③-+-=0; ④·=·; ⑤·=0. 其中正确结论的序号是________. [解析] 容易推出-+-=+=0,所以③正确;又因为底面ABCD是边长为1的正方形,SA=SB=SC=SD=2,所以·=2·2·cos∠ASB,·=2·2·cos∠ 11 CSD,而∠ASB=∠CSD,于是·=·,因此④正确,其余三个都不正确,故正确结论的序号是③④. [答案] ③④ [规律方法] 1.空间向量的线性运算包括加、减及数乘运算,选定空间不共面的三个向量作为基向量,并用它们表示出目标向量,这是用向量法解决立体几何问题的基本要求,解题时可结合已知和所求,根据图形,利用向量运算法则表示所需向量. 2.空间向量的数量积 (1)空间向量的数量积的定义表达式a·b=|a|·|b|·cos〈a,b〉及其变式cos〈a,b〉=是两个重要公式. (2)空间向量的数量积的其他变式是解决立体几何问题的重要公式,如a2=|a|2,a在b上的投影=|a|·cos θ等. [跟踪训练] 1.如图33,已知ABCDA′B′C′D′是平行六面体. 设M是底面ABCD的中心,N是侧面BCC′B′对角线BC′上的分点,设=α+β+γ,则α+β+γ=________. 图33 [连接BD,则M为BD的中点, =+=+=(+)+(+)=(-+)+(+)=++. ∴α=,β=,γ=.∴α+β+γ=.] 11 空间向量的坐标运算 (1)已知a=(2,3,-4),b=(-4,-3,-2),b=x-2a,则x=( ) A.(0,3,-6) B.(0,6,-20) C.(0,6,-6) D.(6,6,-6) (2)已知向量a=(x,1,2),b=(1,y,-2),c=(3,1,z),a∥b,b⊥C. ①求向量a,b,c; ②求a+c与b+c所成角的余弦值. 【导学号:46342183】 [解析] (1)由b=x-2a得x=4a+2b, 又4a+2b=4(2,3,-4)+2(-4,-3,-2)=(0,6,-20), 所以x=(0,6,-20). [答案] B (2)①∵向量a=(x,1,2),b=(1,y,-2),c=(3,1,z),且a∥b,b⊥c, ∴,解得 ∴向量a=(-1,1,2),b=(1,-1,-2),c=(3,1,1). ②∵a+c=(2,2,3),b+c=(4,0,-1), ∴(a+c)·(b+c)=2×4+2×0+3×(-1)=5, |a+c|==,|b+c|==, ∴a+c与b+c所成角的余弦值为=. [规律方法] 熟记空间向量的坐标运算公式 设a=(x1,y1,z1),b=(x2,y2,z2), (1)加减运算:a±b=(x1±x2,y1±y2,z1±z2). (2)数量积运算:a·b=x1x2+y1y2+z1z2. (3)向量夹角:cos〈a,b〉=. (4)向量长度:设M1(x1,y1,z1),M2(x2,y2,z2),则||=. 提醒:在利用坐标运算公式时注意先对向量式子进行化简再运算. [跟踪训练] 2.在空间直角坐标系中,已知点A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC一定是( ) 11 A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形 C [∵=(3,4,-8),=(5,1,-7),=(2,-3,1),∴||==,||==,||==,∴||2+||2=||2,∴△ABC一定为直角三角形.] 利用空间向量证明平行、垂直问题 在四棱锥PABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点. (1)求证:BM∥平面PAD; (2)平面PAD内是否存在一点N,使MN⊥平面PBD?若存在,确定N的位置;若不存在,说明理由. [思路探究] (1)证明向量垂直于平面PAD的一个法向量即可; (2)假设存在点N,设出其坐标,利用⊥,⊥,列方程求其坐标即可. [解] 以A为原点,以AB,AD,AP分别为x轴、y轴、z轴建立空间直角坐标系如图所示,则B(1,0,0),D(0,2,0),P(0,0,2),C(2,2,0),M(1,1,1), (1)证明:∵=(0,1,1), 平面PAD的一个法向量为n=(1,0,0), ∴·n=0,即⊥n, 又BM⊄平面PAD,∴BM∥平面PAD. (2)=(-1,2,0),=(1,0,-2), 假设平面PAD内存在一点N,使MN⊥平面PBD. 设N(0,y,z),则=(-1,y-1,z-1), 从而MN⊥BD,MN⊥PB, ∴即 11 ∴∴N,∴在平面PAD内存在一点N,使MN⊥平面PBD. [规律方法] 利用空间向量证明空间中的位置关系 (1)线线平行: 证明两条直线平行,只需证明两条直线的方向向量是共线向量. (2)线线垂直: 证明两条直线垂直,只需证明两直线的方向向量垂直. (3)线面平行: ①证明直线的方向向量与平面的法向量垂直; ②证明可在平面内找到一个向量与直线的方向向量是共线向量; ③利用共面向量定理,即证明直线的方向向量可用平面内两不共线向量线性表示. (4)线面垂直: ①证明直线的方向向量与平面的法向量平行; ②利用线面垂直的判定定理转化为线线垂直问题. (5)面面平行: ①证明两个平面的法向量平行(即是共线向量); ②转化为线面平行、线线平行问题. (6)面面垂直: ①证明两个平面的法向量互相垂直; ②转化为线面垂直、线线垂直问题. [跟踪训练] 3.如图34,长方体ABCDA1B1C1D1中,点M,N分别在BB1,DD1上,且AM⊥A1B,AN⊥A1D. 图34 (1)求证:A1C⊥平面AMN. (2)当AB=2,AD=2,A1A=3时,问在线段AA1上是否存在一点P使得C1P∥平面AMN,若存在,试确定P的位置. 【导学号:46342184】 11 [解] (1)证明:因为CB⊥平面AA1B1B,AM⊂平面AA1B1B, 所以CB⊥AM,又因为AM⊥A1B,A1B∩CB=B, 所以AM⊥平面A1BC, 所以A1C⊥AM, 同理可证A1C⊥AN, 又AM∩AN=A, 所以A1C⊥平面AMN. (2)以C为原点,CD所在直线为x轴,CB所在直线为y轴,CC1所在直线为z轴,建立空间直角坐标系, 因为AB=2,AD=2,A1A=3, 所以C(0,0,0),A1(2,2,3),C1(0,0,3),=(2,2,3), 由(1)知CA1⊥平面AMN, 故平面AMN的一个法向量为=(2,2,3). 设线段AA1上存在一点P(2,2,t),使得C1P∥平面AMN,则=(2,2,t-3), 因为C1P∥平面AMN, 所以·=4+4+3t-9=0, 解得t=.所以P, 所以线段AA1上存在一点P,使得C1P∥平面AMN. 利用空间向量求空间角 如图35,在等腰直角三角形ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,CD=BE=,O为BC的中点.将△ADE沿DE折起,得到如图(2)所示的四棱锥A′BCDE,其中A′O=. 11 (1) (2) 图35 (1)证明:A′O⊥平面BCDE; (2)求二面角A′CDB的平面角的余弦值. [思路探究] (1)利用勾股定理可证A′O⊥OD,A′O⊥OE,从而证得A′O⊥平面BCDE;(2)用“三垂线”法作二面角的平面角后求解或用向量法求两个平面的法向量的夹角. [解] (1)证明:由题意,得OC=3,AC=3,AD=2. 如图,连接OD,OE,在△OCD中,由余弦定理,得 OD==. 由翻折不变性,知A′D=2, 所以A′O2+OD2=A′D2,所以A′O⊥OD. 同理可证A′O⊥OE. 又因为OD∩OE=O,所以A′O⊥平面BCDE. (2)如图,过点O作OH⊥CD交CD的延长线于点H,连接A′H. 因为A′O⊥平面BCDE,OH⊥CD, 所以A′H⊥CD. 所以∠A′HO为二面角A′CDB的平面角. 结合图(1)可知,H为AC的中点,故OH=, 从而A′H==. 所以cos∠A′HO==. 所以二面角A′CDB的平面角的余弦值为. [规律方法] 用向量法求空间角的注意点 11 (1)异面直线所成角:两异面直线所成角的范围为0°<θ≤90°,需找到两异面直线的方向向量,借助方向向量所成角求解. (2)直线与平面所成的角:要求直线a与平面α所成的角θ,先求这个平面α的法向量n与直线a的方向向量a夹角的余弦cos〈n,a〉,易知θ=〈n,a〉-或者-〈n,a〉. (3)二面角:如图36,有两个平面α与β,分别作这两个平面的法向量n1与n2,则平面α与β所成的角跟法向量n1与n2所成的角相等或互补,所以首先应判断二面角是锐角还是钝角. 图36 [跟踪训练] 4.在如图37所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线. 图37 (1)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC. (2)已知EF=FB=AC=2,AB=BC,求二面角FBCA的余弦值. 【导学号:46342185】 [解] (1)证明:设CF的中点为I,连接GI,HI. 在△CEF中,因为点G,I分别是CE,CF的中点, 所以GI∥EF. 又EF∥OB,所以GI∥OB. 在△CFB中,因为H,I分别是FB,CF的中点, 所以HI∥BC. 又HI∩GI=I,BC∩OB=B, 11 所以平面GHI∥平面ABC. 因为GH⊂平面GHI, 所以GH∥平面ABC. (2)连接OO′,则OO′⊥平面ABC. 又AB=BC,且AC是圆O的直径, 所以BO⊥AC. 以O为坐标原点,建立如图所示的空间直角坐标系. 由题意得B(0,2,0),C(-2,0,0). 过点F作FM⊥OB于点M, 所以FM==3, 可得F(0,,3). 故=(-2,-2,0),=(0,-,3). 设m=(x,y,z)是平面BCF的法向量. 由 可得 可得平面BCF的一个法向量m=. 因为平面ABC的一个法向量n=(0,0,1), 所以cos〈m,n〉==, 所以二面角FBCA的余弦值为. 11查看更多