云南省大理州2020届高三11月统测试题 数学（理）

云南省大理州2020届高三11月统测试题 数学（理）

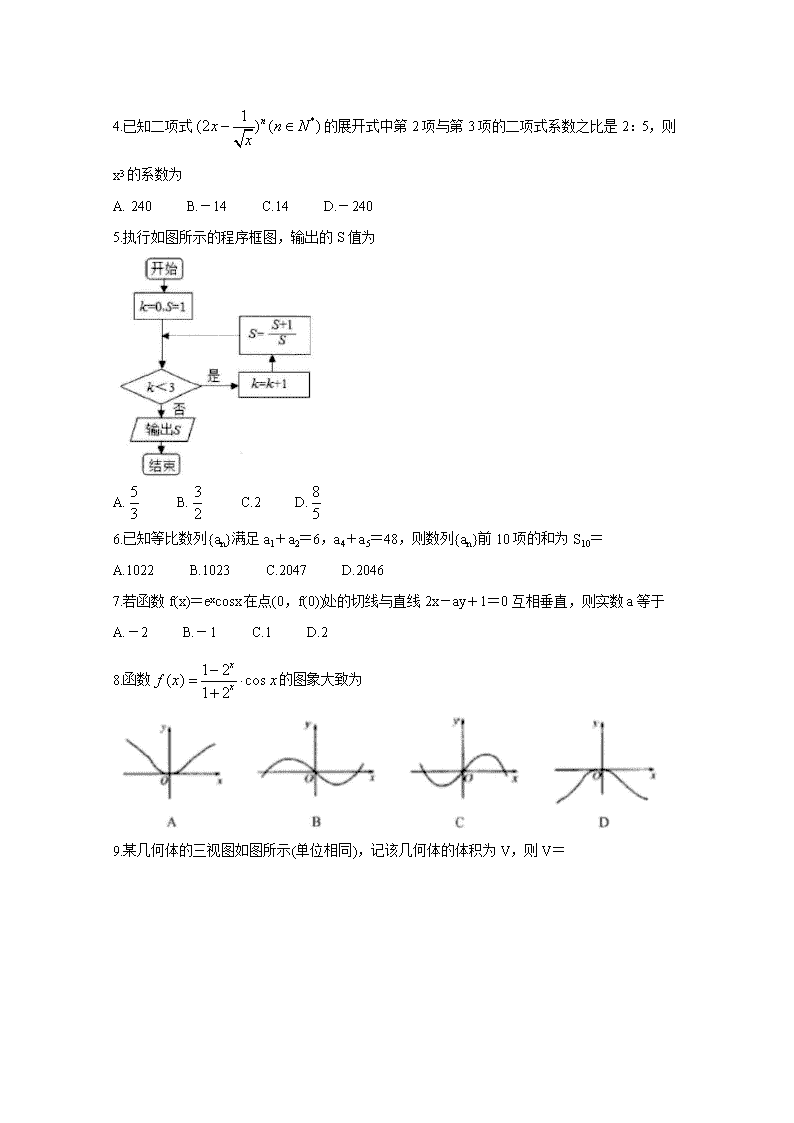
理科数学 ‎ 本试卷满分150分，考试时间120分钟 考生注意：‎ ‎1.答卷前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号填写在答题卡上，并认真核准条形码上的准考证号、姓名、考场号、座位号及科目，在规定的位置贴好条形码。‎ ‎2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。‎ ‎3.考试结束后，将本试卷和答题卡一并交回。‎ 一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.已知集合A＝{1，2，3}，B＝{x|(x＋1)(x－2)＜0，x∈Z}，则A∪B等于 A.{1} B.{1，2} C.{0，1，2，3} D.{－1，0，1，2，3}‎ ‎2.设复数z满足(1＋i)z＝2i，则|z|＝‎ A. B. C. D.2‎ ‎3.某教育局为了解“跑团”每月跑步的平均里程，收集并整理了2017年1月至2017年11月期间“跑团”每月跑步的平均里程(单位：公里)的数据，绘制了下面的折线图。根据折线图，下列结论正确的是 A.月跑步平均里程的中位数为6月份对应的里程数 B.月跑步平均里程逐月增加 C.月跑步平均里程高峰期大致在8、9月 D.1月至5月的月跑步平均里程相对于6月至11月，波动性更小，变化比较平稳 ‎4.已知二项式的展开式中第2项与第3项的二项式系数之比是2：5，则x3的系数为 A. 240 B.－14 C.14 D.－240‎ ‎5.执行如图所示的程序框图，输出的S值为 A. B. C.2 D.‎ ‎6.已知等比数列{an}满足a1＋a2＝6，a4＋a5＝48，则数列{an}前10项的和为S10＝‎ A.1022 B.1023 C.2047 D.2046‎ ‎7.若函数f(x)＝excosx在点(0，f(0))处的切线与直线2x－ay＋1＝0互相垂直，则实数a等于 A.－2 B.－1 C.1 D.2‎ ‎8.函数的图象大致为 ‎ ‎ ‎9.某几何体的三视图如图所示(单位相同)，记该几何体的体积为V，则V＝‎ A. B.243 C. D.729‎ ‎10.设F是双曲线C：的一个焦点，若C上存在点P，使线段PF的中点恰为虚轴的一个端点，则C的离心率为 A.2 B. C.5 D.‎ ‎11.设函数f(x)＝ex＋x－2，g(x)＝lnx＋x2－3。若实数a，b满足f(a)＝0，g(b)＝0，则 A.0＜g(a)＜f(b) B.f(b)＜0＜g(a) C.g(a)＜0＜f(b) D.f(b)＜g(a)＜0‎ ‎12.已知定义域为R的函数f(x)对任意实数x，y满足：，且f(0)＝f(1)＝0，，并且当x∈(0，)时，f(x)＞0。给出如下结论：‎ ‎①函数f(x)是偶函数； ②函数f(x)在(－，)上单调递增；‎ ‎③函数f(x)是以2为周期的周期函数； ④f(－)＝0。‎ 其中正确的结论是 A.①② B.②③ C.①④ D.③④‎ 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13.若向量满足||＝，||＝2，⊥(－)，则与的夹角为 。‎ ‎14.已知等差数列{an}的前n项为Sn，且a1＋a5＝－14，S9＝－27，则使得Sn取最小值时的n为 。‎ ‎15.在三棱锥P－ABC中，平面PAB⊥平面ABC，△ABC是边长为6的等边三角形，△PAB是以AB为斜边的等腰直角三角形，则该三棱锥外接球的表面积为 。‎ ‎16.在平面直角坐标系xOy中，已知圆C：(x－1)2＋(y－2)2＝16，若等腰直角△PAB的斜边AB为圆C的一条弦，则|PC|的最大值为 。‎ 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎(一)必考题：共60分。‎ ‎17.(12分)‎ 为更好地落实农民工工资保证金制度，南方某市劳动保障部门调查了2018年下半年该市100名农民工(其中技术工、非技术工各50名)的月工资，得到这100名农民工的月工资均在[25，55](百元)内，且月工资收入在[45，50)(百元)内的人数为15，并根据调查结果画出如图所示的频率分布直方图：‎ ‎(1)求n的值；‎ ‎(2)已知这100名农民工中月工资高于平均数的技术工有31名，非技术工有19名。‎ ‎①完成如下所示2×2列联表 ‎②则能否在犯错误的概率不超过0.001的前提下认为是不是技术工与月工资是否高于平均数有关系？‎ 参考公式及数据：，其中n＝a＋b＋c＋d。‎ ‎18.(12分)‎ 已知△ABC的内角A，B，C的对边分别为a，b，c。‎ ‎(1)若A＝，a＝3，C＝，求b；‎ ‎(2)若A＝，a＝2，求△ABC的周长的范围。‎ ‎19.(12分)‎ 如图，在直三棱柱ABC－A1B1C1中，AC＝BC＝2，D为棱CC1的中点，AB1∩A1B＝O。‎ ‎ ‎ ‎(1)证明：C1O∥平面ABD；‎ ‎(2)设二面角D－AB－C的正切值为，AC⊥BC，，求异面直线C1O与CE所成角的余弦值。‎ ‎20.(12分)‎ 已知函数在[1，＋∞)上为增函数，且θ∈(0，π)，，(其中m∈R)。‎ ‎(1)求θ的值；‎ ‎(2)设，若存在x0∈[1，e]，使得f(x0)－g(x0)＞h(x0)成立，求m的取值范围。‎ ‎21.(12分)‎ 已知P(－3，0)，椭圆C：的离心率为，直线l与C交于A，B两点，AB长度的最大值为4。‎ ‎(1)求C的方程；‎ ‎(2)直线l与x轴的交点为M，当直线l变化(l不与x轴重合)时，若|MA||PB|＝|MB||PA|，求点M的坐标。‎ ‎(二)选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。‎ ‎22.[选修4－4：坐标系与参数方程](本小题满分10分)‎ 在极坐标系中，射线l：θ＝与圆C：ρ＝2交于点A，椭圆Γ的方程为：，以极点为原点，极轴为x轴正半轴建立平面直角标系xOy。‎ ‎(1)求点A的直角坐标和椭圆Γ的参数方程；‎ ‎(2)若B为椭圆Γ的下顶点，M为椭圆Γ上任意一点，求的最大值。‎ ‎23. [选修4－5：不等式选讲](本小题满分10分)‎ 已知a＞0，b＞0，a3＋b3＝2。证明：‎ ‎(1)(a＋b)(a5＋b5)≥4；‎ ‎(2)a＋b≤2。‎