- 2021-04-17 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020_2021学年新教材高中数学第7章三角函数7
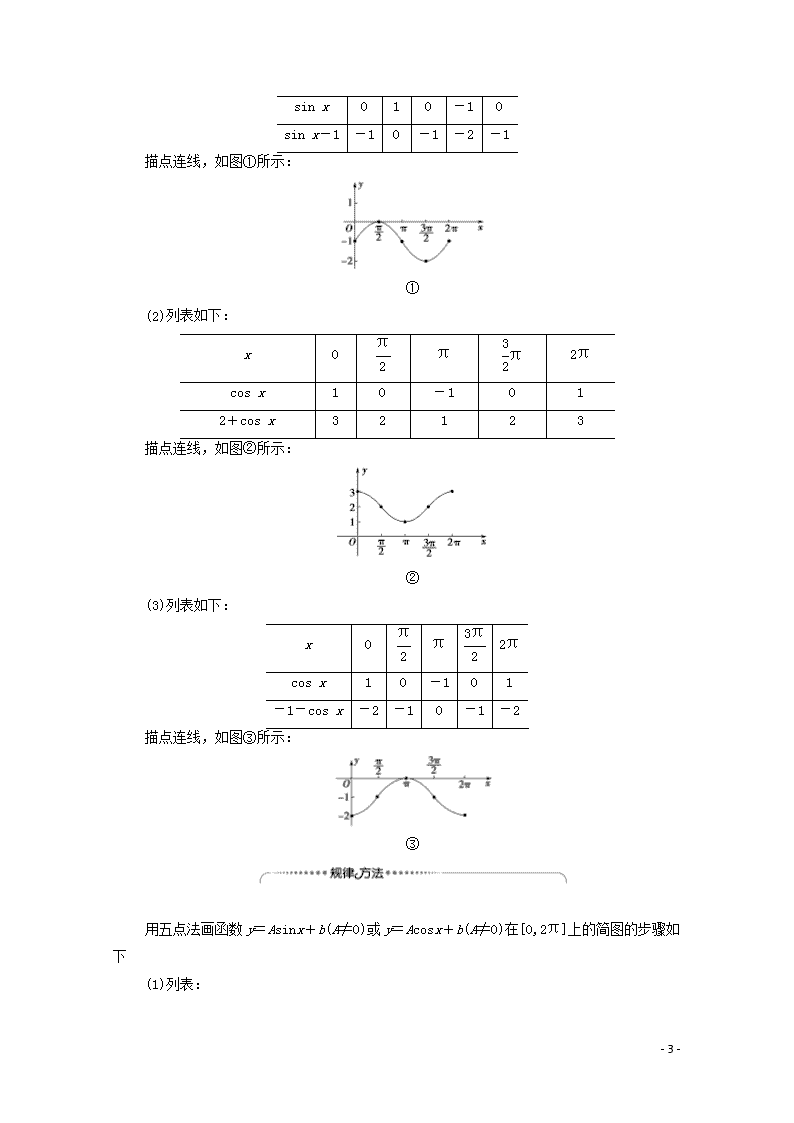
7.3.2 三角函数的图象与性质 第1课时 正弦、余弦函数的图象 学 习 目 标 核 心 素 养 1.了解正弦函数、余弦函数的图象. 2.会用“五点法”画出正弦函数、余弦函数的图象.(重点) 3.借助图象理解正弦函数、余弦函数在[0,2π]上的性质.(重点、难点) 通过学习本节内容,培养学生的直观想象的核心素养. 网上百度一下一个物理实验:“沙摆实验”视频,就是将一个装满细砂的漏斗挂在一个铁架上做单摆运动时,沙子落在与单摆运动方向垂直的木板上,我们通过实验看看落在木板上的细砂轨迹是什么? 1.正弦曲线、余弦曲线 正弦函数y=sin x(x∈R)和余弦函数y=cos x(x∈R)的图象分别叫作正弦曲线和余弦曲线(如图). 2.“五点法”画图 画正弦函数y=sin x,x∈[0,2π]的图象,五个关键点是(0,0),,(π,0),,(2π,0). - 8 - 画余弦函数y=cos x,x∈[0,2π]的图象,五个关键点是(0,1),,(π,-1),,(2π,1). 3.正弦、余弦曲线的联系 依据诱导公式cos x=sin,要得到y=cos x的图象,只需把y=sin x的图象向左平移个单位长度即可. 思考:作正、余弦函数的图象时,函数自变量能用角度制吗? [提示] 作图象时,函数自变量要用弧度制,自变量与函数值均为实数,因此在x轴、y轴上可以统一单位,这样作出的图象正规便于应用. 1.思考辨析(正确的打“√”,错误的打“×”) (1)正弦曲线的图象向左右无限延展. ( ) (2)y=sin x与y=cos x的图象形状相同,只是位置不同. ( ) (3)函数y=cos x的图象与y轴只有一个交点. ( ) [答案] (1)√ (2)√ (3)√ 2.用“五点法”作y=2sin 2x的图象时,首先描出的五个点的横坐标是________. [答案] 0,,,,π 3.不等式cos x<0,x∈[0,2π]的解集为________. [答案] 利用“五点法”作简图 【例1】 用“五点法”作出下列函数的图象. (1)y=sin x-1,x∈[0,2π]; (2)y=2+cos x,x∈[0,2π]; (3)y=-1-cos x,x∈[0,2π]. [思路点拨] 先分别取出相应函数在[0,2π]上的五个关键点,再描点连线. [解] (1)列表如下: x 0 π π 2π - 8 - sin x 0 1 0 -1 0 sin x-1 -1 0 -1 -2 -1 描点连线,如图①所示: ① (2)列表如下: x 0 π π 2π cos x 1 0 -1 0 1 2+cos x 3 2 1 2 3 描点连线,如图②所示: ② (3)列表如下: x 0 π 2π cos x 1 0 -1 0 1 -1-cos x -2 -1 0 -1 -2 描点连线,如图③所示: ③ 用五点法画函数y=Asin x+b(A≠0)或y=Acos x+b(A≠0)在[0,2π]上的简图的步骤如下 (1)列表: - 8 - x 0 π 2π sin x(或cos x) y (2)描点:在平面直角坐标系中描出下列五个点:(0,y),,(π,y),,(2π,y),这里的y是通过函数式计算得到的. (3)连线:用光滑的曲线将描出的五个点连接起来,不要用线段进行连接. 提醒:对于正、余弦函数的图象问题,要画出正确的正弦曲线、余弦曲线,掌握两者的形状相同,只是在坐标系中的位置不同,可以通过相互平移得到. 1.用“五点法”作出函数y=3+2cos x在一个周期内的图象. [解] 按五个关键点列表、描点,并将它们用光滑的曲线连接起来. x 0 π 2π cos x 1 0 -1 0 1 3+2cos x 5 3 1 3 5 利用正、余弦曲线解三角不等式 【例2】 利用正弦曲线,求满足<sin x≤的x的集合. [思路点拨] 作出正弦函数y=sin x在一个周期内的图象,然后借助图象求解. [解] 首先作出y=sin x在[0,2π]上的图象,如图所示, - 8 - 作直线y=,根据特殊角的正弦值,可知该直线与y=sin x,x∈[0,2π]的交点横坐标为和;作直线y=,该直线与y=sin x,x∈[0,2π]的交点横坐标为和.观察图象可知,在[0,2π]上,当<x≤,或≤x<时,不等式<sin x≤成立, 所以<sin x≤的解集为. 利用正弦曲线、余弦曲线解三角不等式的一般步骤 (1)画出正弦函数y=sin x或余弦函数y=cos x在[0,2π]上的图象; (2)写出适合不等式在区间[0,2π]上的解集; (3)把此解集推广到整个定义域上去. 2.求下列函数的定义域: (1)y=;(2)y=. [解] (1)要使y=有意义,则必须满足2sin x+1≥0,即sin x≥-. 结合正弦曲线或三角函数线, 如图所示,知函数y=的定义域为 . (2)要使函数有意义,必须满足sin x-cos x≥0. 在同一坐标系中画出[0,2π]上y=sin x和y=cos x的图象,如图所示. 在[0,2π]内,满足sin x=cos x的x为, - 8 - ,再结合正弦、余弦函数的图象,知所求定义域为. 正、余弦函数图象的应用 [探究问题] 1.你能借助图象的变换作出y=|sin x|的图象吗?试画出其图象. [提示] 先画出y=sin x的图象,然后将其x轴下方的部分对称到x轴的上方(x轴上方的保持不变)即可得到y=|sin x|的图象,如图. 2.方程|sin x|=a,a∈R在[0,2π]上有几解? [提示] 当a<0时,方程|sin x|=a无解; 当a=0时,方程|sin x|=a有三解; 当0<a<1时,方程|sin x|=a有四解; 当a=1时,方程|sin x|=a有两解; 当a>1时,方程|sin x|=a无解. 【例3】 在同一坐标系中,作函数y=sin x和y=lg x的图象,根据图象判断出方程sin x=lg x的解的个数. [思路点拨] ―→―→ ―→ [解] 建立直角坐标系xOy,先用五点法画出函数y=sin x,x∈[0,2π]的图象,再依次向右连续平移2π个单位,得到y=sin x的图象. 描出点,(1,0),(10,1),并用光滑曲线连接得到y=lg x的图象,如图所示. 由图象可知方程sin x=lg x的解有3个. 1.利用三角函数图象能解决求方程解的个数问题,也可利用方程解的个数(或两函数图象的交点个数)求参数的范围问题. 2.常见的函数图象变换 - 8 - (1)y=f(x) 的图象向左(右)平移a个单位,得到函数y=f(x+a)[y=f(x-a)]的图象; (2)y=f(x)的图象向上(下)平移b个单位,得到函数y=f(x)+b[y=f(x)-b]的图象; (3)y=f(x)的图象作关于x轴对称的图象,得到函数y=-f(x)的图象; (4)y=f(x)的图象作关于y轴对称的图象,得到函数y=f(-x)的图象; (5)y=f(x)的图象作关于原点对称的图象,得到函数y=-f(-x)的图象; (6)y=f(x)的图象保留x轴及其上方的图象,同时x轴下方的图象作关于x轴对称的图象,得到函数y=|f(x)|的图象; (7)y=f(x)的图象保留y轴及其右侧的图象,再去掉y轴左侧的图象,最后y轴右侧的图象作关于y轴对称的图象,得函数y=f(|x|)的图象. 3.函数f(x)=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,求k的取值范围. [解] f(x)=的图象如图所示,故由图象知1<k<3. 1.本节课的重点是“五点法”作正弦函数和余弦函数的图象,难点是图象的应用. 2.本节课要重点掌握正、余弦函数图象的三个问题 (1)正、余弦函数图象的画法. (2)利用正、余弦函数的图象解不等式. (3)正、余弦曲线与其他曲线的交点问题. 3.本节课要牢记正、余弦函数图象中五点的确定 y=sin x,x∈[0,2π]与y=cos x,x∈[0,2π]的图象上的关键五点分为两类:①图象与x轴的交点;②图象上的最高点和最低点.其中,y=sin x,x∈[0,2π]与x轴有三个交点:(0,0),(π,0),(2π,0),图象上有一个最高点,一个最低点;y=cos x,x∈[0,2π]与x轴有两个交点:, - 8 - ,图象上有两个最高点:(0,1),(2π,1),一个最低点(π,-1). 1.用“五点法”作出函数y=3-cos x的图象,下列点中不属于五点作图中的五个关键点的是________.(填序号) ①(π,-1);②(0,2);③;④(π,4);⑤. ①⑤ [由五点作图法知五个关键点分别为(0,2),,(π,4),,(2π,2),故①⑤不是关键点.] 2.函数y=sin x与函数y=-sin x的图象关于________对称. x轴 [在同一坐标系中画出函数y=sin x与函数y=-sin x的图象(图略),可知它们关于x轴对称.] 3.sin x>0,x∈[0,2π]的解集是________. (0,π) [如图所示是y=sin x,x∈[0,2π]的图象, 由图可知满足sin x>0,x∈[0,2π]的解集是(0,π).] 4.用“五点法”作出y=(0≤x≤2π)的简图. [解] y==|cos x|(x∈[0,2π]). 列表: x 0 π 2π cos x 1 0 -1 0 1 |cos x| 1 0 1 0 1 1 0 1 0 1 描点作图,如图. - 8 -查看更多