- 2021-04-17 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
顺义区2012年初三数学统一练习
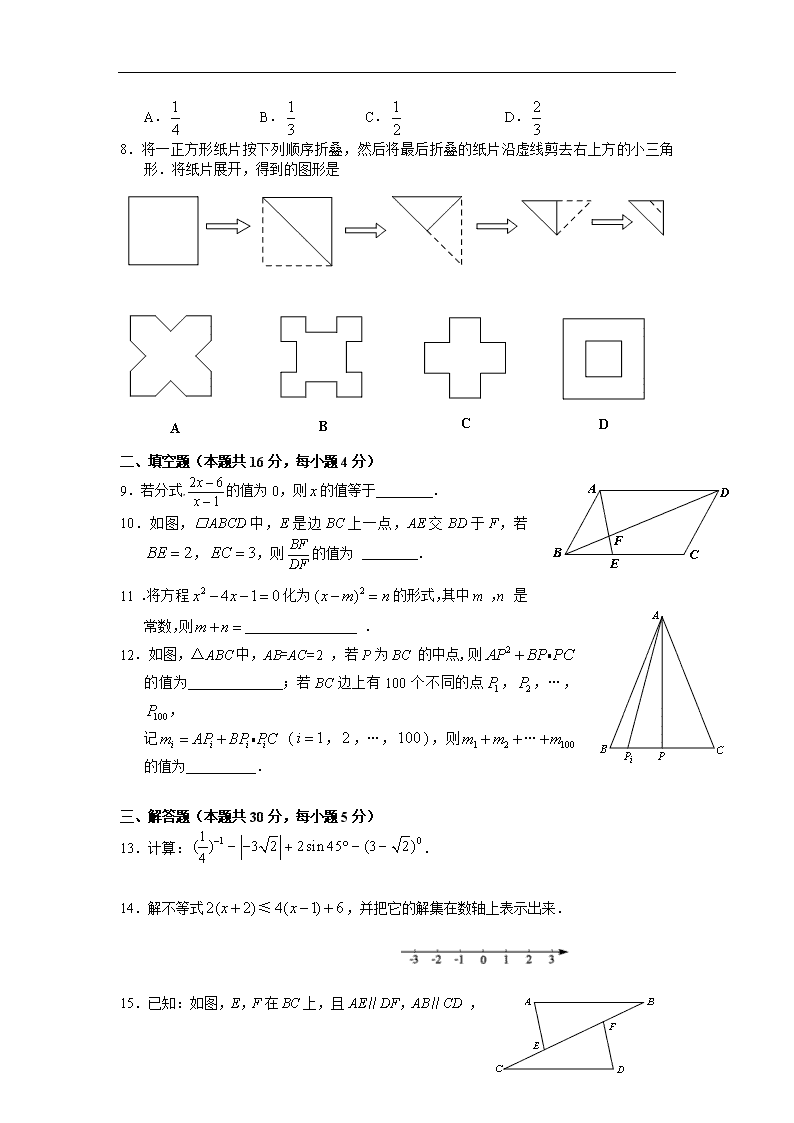
顺义区2012届初三第二次统一练习 数学试卷 考生须知 1.本试卷共5页,共五道大题,25道小题,满分120分.考试时间120分钟. 2.在试卷和答题卡上准确填写学校名称、姓名和准考证号. 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效. 4.在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答. 5.考试结束,将本试卷、答题卡和草稿纸一并交回. 一、选择题(本题共32分,每小题4分) 下面各题均有四个选项,其中只有一个是符合题意的. 1.9的平方根是( ) A.3 B.-3 C. D. 2.据人民网报道,“十一五”我国铁路营业里程达9.1万公里.请把9.1万用科学记数法表示应为 A. B. C. D. 3.如图,下列选项中不是正六棱柱三视图的是( ) A B C D 4.把分解因式,结果正确的是( ) A. B. C. D. 5.北京是严重缺水的城市,市政府号召居民节约用水,为了解居民用水情况,小敏在某小区随机抽查了10户家庭的5月份用水量,结果如下(单位:立方米):5,6,6,2,5,6,7,10,7,6,则关于这10户家庭的5月份用水量,下列说法错误的是( ) A.众数是6 B.极差是8 C.平均数是6 D.方差是4 6.如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA、OB 在O点钉在一起,并使它们保持互相垂直.在测直径时,把O点靠在圆周上 ,读得刻度OE=4个单位,OF=3个单位,则圆的直径为( ) A.7个单位 B.6个单位 C.5个单位 D.4个单位 7.从1,-2, 3,-4四个数中,随机抽取两个数相乘,积是正数的概率是 A. B. C. D. 8.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去右上方的小三角形.将纸片展开,得到的图形是 二、填空题(本题共16分,每小题4分) 9.若分式的值为0,则的值等于 . 10.如图,□ABCD中,E是边BC上一点,AE交BD于F,若,,则的值为 . 11.将方程化为的形式,其中m,n是常数,则 . 12.如图,△ABC中,AB=AC=2 ,若P为BC 的中点,则的值为 ;若BC边上有100个不同的点,,…,, 记,,…,,则…的值为 . 三、解答题(本题共30分,每小题5分) 13.计算:. 14.解不等式≤,并把它的解集在数轴上表示出来. 15.已知:如图,E,F在BC上,且AE∥DF,AB∥CD , AB=CD. 求证:BF = CE . 16.解分式方程:. 17.已知2x-3=0,求代数式的值. 18.某市实施“限塑令”后,2008年大约减少塑料消耗约4万吨.调查分析结果显示,从2008年开始,五年内该市因实施“限塑令”而减少的塑料消耗量y(万吨)随着时间(年)逐年成直线上升,y与之间的关系如图所示. (1)求y与之间的关系式; (2)请你估计,该市2011年因实施“限塑令”而减少的塑料消耗量为多少? 四、解答题(本题共20分,每小题5分) 19.如图,在矩形ABCD中,E是边CB延长线上的点,且EB=AB,DE与AB相交于点F, AD=2,CD=1,求AE及DF的长. 20.已知:如图,P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,BC∥OP交⊙O于点C. (1)判断直线PC与⊙O的位置关系,并证明你的结论; (2)若BC=2,,求PC的长及点C到PA的距离. 21.阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,每年的4月23日被联合国教科文组织确定为“世界读书日”.某校倡导学生读书,下面的表格是学生阅读课外书籍情况统计表,图1是该校初中三个年级学生人数分布的扇形统计图,其中八年级学生人数为204人,请你根据图表中提供的信息,解答下列问题: 图书种类 频数 频率 科普常识 840 b 名人传记 816 0.34 中外名著 a 0.25 其他 144 0.06 (1)求该校八年级学生的人数占全校学生总人数的百分比; (2)求表中a,b的值; (3)求该校学生平均每人读多少本课外书? 22.阅读下列材料:[来源:Z§xx§k.Com] 问题:如图1,P为正方形ABCD内一点,且PA∶PB∶PC=1∶2∶3,求∠APB的度数. 小娜同学的想法是:不妨设PA=1, PB=2,PC=3,设法把PA、PB、PC相对集中,于是他将△BCP绕点B顺时针旋转90°得到△BAE(如图2),然后连结PE,问题得以解决. 请你回答:图2中∠APB的度数为 . 请你参考小娜同学的思路,解决下列问题: 如图3,P是等边三角形ABC内一点,已知∠APB=115°,∠BPC=125°. (1)在图3中画出并指明以PA、PB、PC的长度为三边长的一个三角形(保留画图痕迹); (2)求出以PA、PB、PC的长度为三边长的三角形的各内角的度数分别等于 . 图1 图2 图3 五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.如图,直线AB经过第一象限,分别与x轴、y轴交于A、B两点,P为线段AB上任意一点(不与A、B重合),过点P分别向x轴、y轴作垂线,垂足分别为C、D.设OC=x,四边形OCPD的面积为S. (1)若已知A(4,0),B(0,6),求S与x之间的函数关系式; (2)若已知A(a,0),B(0,b),且当x=时,S有最大值,求直线AB的解析式; (3)在(2)的条件下,在直线AB上有一点M,且点M到x轴、y轴的距离相等,点N在过M点的反比例函数图象上,且△OAN是直角三角形,求点N的坐标. 24.已知:如图,D为线段AB上一点(不与点A、B重合),CD⊥AB,且CD=AB,AE⊥AB,BF⊥AB,且AE=BD,BF=AD. (1)如图1,当点D恰是AB的中点时,请你猜想并证明∠ACE与∠BCF的数量关系; (2)如图2,当点D不是AB的中点时,你在(1)中所得的结论是否发生变化,写出你的猜想并证明; (3)若∠ACB=,直接写出∠ECF的度数(用含的式子表示). 图1 图2 25.如图,在平面直角坐标系xOy中,二次函数的图象经过点A(-3,6),并与x轴交于点B(-1,0)和点C,顶点为P. (1)求二次函数的解析式; (2)设D为线段OC上的一点,若,求点D的坐标; (3)在(2)的条件下,若点M在抛物线上,点N在y轴上,要使以M、N、B、D为顶点的四边形是平行四边形,这样的点M、N是否存在,若存在,求出所有满足条件的点M的坐标;若不存在,说明理由. 顺义区2012届初三第二次统一练习 数学学科参考答案及评分细则 一、选择题(本题共32分,每小题4分) 题 号 1 2 3 4 5 6 7 8 答 案 C B A D D C B A 二、填空题(本题共16分,每小题4分,) 9.; 10.; 11.7; 12.,. 三、解答题(本题共30分,每小题5分) 13.解: …………………………………………………… 4分 …………………………………………………………………… 5分 14.解:去括号,得 ≤.…………………………………………… 1分 移项,得 ≤.…………………………………………… 2分 合并,得 ≤-2 . ………………………………………… 3分 系数化为1,得 ≥ . ……………………………………………… 4分 不等式的解集在数轴上表示如下: ……………………………………… 5分 15.证明:∵ AE∥DF, ∴∠1=∠2. ………………………… 1分 ∵ AB∥CD, ∴ ∠B=∠C.………………………… 2分 在△ABE和 △DCF中, ∴ △ABE≌△DCF.…………………………………………………… 4分 ∴ BE=CF. ∴BE-EF=CF-EF. 即BF=CE.……………………………………………………………… 5分 16.解:去分母,得 .…………………… 1分 去括号,得 . ………………………… 2分 整理,得 .…………………………………………………… 3分 解得 . ……………………………………………………………… 4分 经检验,是原方程的解.……………………………………………… 5分 ∴ 原方程的解是. 17.解: ……………………………………………… 2分 ………………………………………………………………… 3分 …………………………………………………………… 4分 当2x-3=0时,原式.………………………………… 5分 18.解:(1)设y与之间的关系式为y=kx+b.……………………………………… 1分 由题意,得 解得 …………………… 3分 ∴y与之间的关系式为y=x-2004(2008≤x≤2012). …………… 4分 (2)当x=2012时,y=2012-2004=8. ∴该市2012年因“限塑令”而减少的塑料消耗量约为8万吨.……… 5分 19.解:∵四边形ABCD是矩形,且AD=2,CD=1, ∴BC=AD=2,AB=CD=1,∠ABC =∠C= 90°,AB∥DC. ∴EB=AB=1. ………………………………………………………………… 1分 在Rt△ABE中,.………………………………… 2分 在Rt△DCE中,.………………… 3分 ∵AB∥DC, ∴. …………………………………………………………… 4分 设,则. ∵, ∴. ∴. ∴.………………………………………………………… 5分 20.解:(1)直线PC与⊙O相切. 证明:连结OC, ∵BC∥OP, ∴∠1 =∠2,∠3=∠4. ∵OB=OC, ∴∠1=∠3. ∴∠2=∠4. 又∵OC=OA,OP=OP, ∴△POC≌△POA. ……………………………………………… 1分 ∴∠PCO =∠PAO. ∵PA切⊙O于点A, ∴∠PAO =90°. ∴∠PCO =90°. ∴PC与⊙O相切. ……………………………………………… 2分 (2)解:∵△POC≌△POA, ∴∠5=∠6=. ∴. ∵∠PCO =90°,∴∠2+∠5=90°. ∴. ∵∠3=∠1 =∠2, ∴. 连结AC, ∵AB是⊙O的直径, ∴∠ACB =90°. ∴.………………………………………… 3分 ∴OA=OB=OC=3,. ∴在Rt△POC中,. ∴.…………………………………… 4分 过点C作CD⊥PA于D, ∵∠ACB =∠PAO =90°, ∴∠3+∠7 =90°,∠7+∠8 =90°. ∴∠3=∠8. ∴. 在Rt△CAD中,. ∴.……………………………………… 5分 21.解:(1)∵1-28%-38%=34%. ∴该校八年级学生的人数占全校学生总人数的百分比为34%.……… 1分 (2)∵, ∴, ……………………………………………… 2分 . ……………………………………………… 3分 (3)∵八年级学生人数为204人,占全校学生总人数的百分比为34%, ∴全校学生总人数为. ……………………………… 4分 ∴该校学生平均每人读课外书:. 答:该校学生平均每人读4本课外书. ………………………………… 5分 22.解:图2中∠APB的度数为 135° .……………… 1分 (1)如图3,以PA、PB、PC的长度为三边长的 一个三角形是 △APM .(含画图)………… 2分 (2)以PA、PB、PC的长度为三边长的[来源:学科网ZXXK] 三角形的各内角的度数分别等于 60°、65°、55° .……………… 5分 23.解:(1)设直线AB的解析式为, 由A(4,0),B(0,6),得 解得[来源:Z。xx。k.Com] ∴直线AB的解析式为.……………………………… 1分 ∵OC=x,∴. ∴. 即(0< x <4). …………………………………… 2分 (2)设直线AB的解析式为, ∵OC=x,∴. ∴. ∵当x=时,S有最大值, ∴ 解得 ∴直线AB的解析式为.………………………………… 3分 ∴A(,0),B(0,3). 即,.……………………………………………………… 5分 (3)设点M的坐标为(,), 由点M在(2)中的直线AB上, ∴. ∵点M到x轴、y轴的距离相等, ∴或. 当时,M点的坐标为(1,1). 过M点的反比例函数的解析式为. ∵点N在的图象上,OA在x轴上,且△OAN是直角三角形, ∴点N的坐标为.……………………………………………… 6分 当时,M点的坐标为(3,-3), 过M点的反比例函数的解析式为. ∵点N在的图象上,OA在x轴上,且△OAN是直角三角形, ∴点N的坐标为.……………………………………………… 7分 综上,点N的坐标为或. 24.解:(1)猜想:∠ACE=∠BCF.[来源:学*科*网Z*X*X*K] 证明:∵D是AB中点, ∴AD=BD, 又∵AE=BD,BF=AD, ∴AE=BF. ∵CD⊥AB,AD=BD, ∴CA=CB. ∴∠1 =∠2. ∵AE⊥AB,BF⊥AB, ∴∠3 =∠4=90°. ∴∠1+∠3 =∠2+∠4. 即∠CAE=∠CBF. ∴△CAE ≌△CBF. ∴∠ACE=∠BCF.……………………………………………… 2分 (2)∠ACE=∠BCF仍然成立. 证明:连结BE、AF. ∵CD⊥AB,AE⊥AB, ∴∠CDB=∠BAE=90°. 又∵BD = AE,CD = AB , △CDB≌△BAE.……………… 3分 ∴CB=BE,∠BCD=∠EBA. 在Rt△CDB中,∵∠CDB =90°, ∴∠BCD+∠CBD =90°. ∴∠EBA+∠CBD =90°. 即∠CBE =90°. ∴△BCE是等腰直角三角形. ∴∠BCE=45°. ……………………………………………… 4分[来源:Z*xx*k.Com] 同理可证:△ACF是等腰直角三角形. ∴∠ACF=45°. ……………………………………………… 5分 ∴∠ACF=∠BCE. ∴∠ACF-∠ECF =∠BCE-∠ECF. 即∠ACE=∠BCF.……………………………………………… 6分 (3)∠ECF的度数为90°-.……………………………………………… 7分 25.解:(1)将点A(-3,6),B(-1,0)代入中,得 解得 ∴二次函数的解析式为.…………………………… 2分 (2)令,得,解得 ,. ∴点C的坐标为(3,0). ∵, ∴顶点P的坐标为(1,-2).…………………………………………… 3分 过点A作AE⊥x轴,过点P作PF⊥x轴,垂足分别为E,F. 易得 . ,. 又, ∴△ACB∽△PCD.…………………… 4分 ∴. ∵, ∴. ∴. ∴点D的坐标为.……………………………………………… 5分 (3)当BD为一边时,由于, ∴点M的坐标为或. ………………………… 7分 当BD为对角线时,点M的坐标为. …………………… 8分查看更多