高中同步数学教案第11章 坐标平面上的直线

高中同步数学教案第11章 坐标平面上的直线

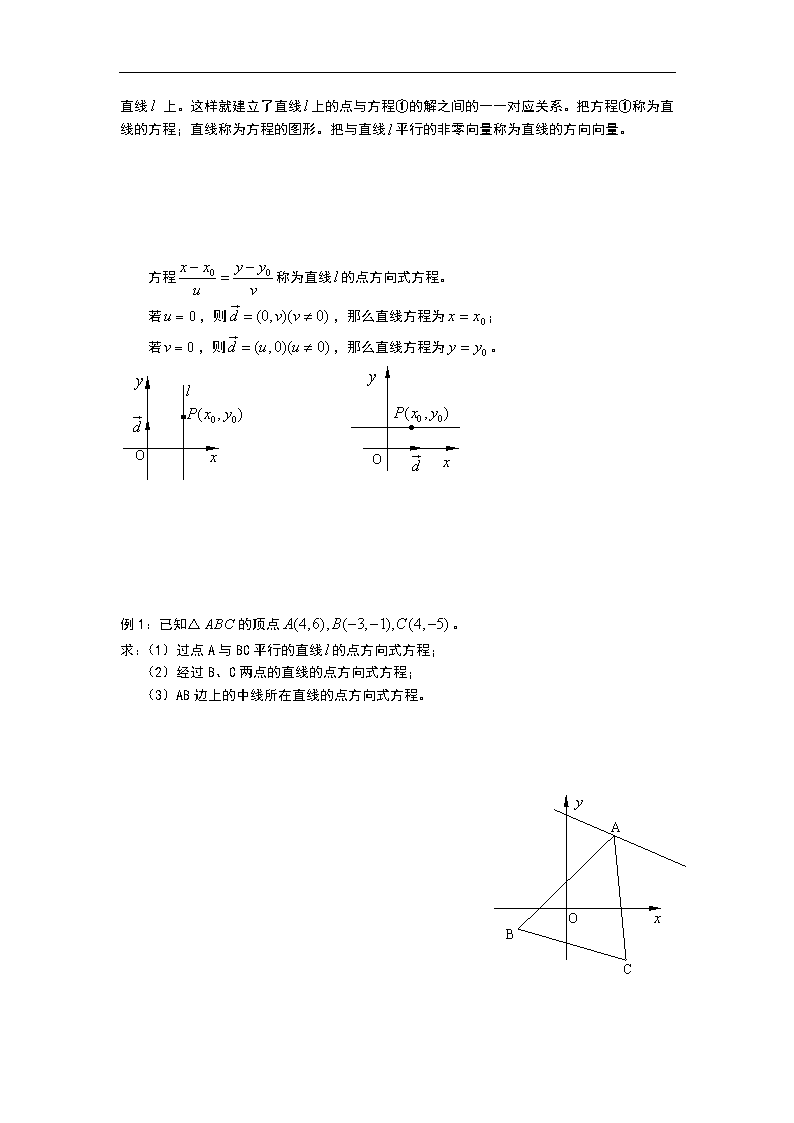
‎ 第十一章：坐标平面上的直线 ‎11、1 直线的方程 ‎1、直线的点方向式方程 已知直线经过某个已知点，且与已知的非零向量平行，那么这样的直线也是唯一确定的（如图）。那么这条直线如何表示呢？解析几何里是用直线上任何一点的坐标满足的关系式来表示这条直线。‎ O 设点是过点P与向量平行的直线上的任意一点（包括，‎ 则，，‎ ‎，当时，‎ 即得 ①‎ 反之，若是方程①的任意一组解，‎ 则有，则向量与向量平行，从而点在直线上。‎ 由此可见：直线所有点的坐标都满足方程①，而以方程①‎ 的所有解为坐标的点都在直线上。这样就建立了直线上的点与方程①的解之间的一一对应关系。把方程①称为直线的方程；直线称为方程的图形。把与直线平行的非零向量称为直线的方向向量。‎ ‎ ‎ ‎ 方程称为直线的点方向式方程。‎ 若，则，那么直线方程为；‎ 若，则，那么直线方程为。‎ O O 例1：已知△的顶点。‎ 求：（1）过点A与BC平行的直线的点方向式方程；‎ ‎ （2）经过B、C两点的直线的点方向式方程；‎ ‎ （3）AB边上的中线所在直线的点方向式方程。‎ A B C O 解：（1）是直线的一个方向向量，‎ 所以直线的方程为。‎ ‎（2）也是直线BC的一个方向向量，所以直线BC的点方向式方程为：‎ ‎　　　　，（或）‎ ‎（3）AB中点坐标是，是它的一个方向向量，，‎ 所以AB边上中线所在直线的方程为：。‎ 注意：（1）一般地，经过两点，PQ与坐标轴不平行的直线的点方向式方程为。此方程也称为直线的两点式方程。‎ ‎（2）若直线经过两点，则直线的方程为，整理得：。（此方程称直线的截距式）。‎ ‎2、直线的点法向式方程 已知直线经过点，且与非零向量垂直，求直线的方程。‎ O 如图：设是直线上的任意一点，由题意知：‎ ‎，由向量垂直的充要条件知，。‎ 又，‎ 所以　　②‎ 反之，如果是方程②的解，即，那么以为起点、为终点的向量与向量的数量积为零。可知，于是点在直线上。‎ 向量叫做直线的法向量，方程②称为直线的点法向式方程。‎ 例2：已知点和点，求直线AB的垂直平分线的点法式方程。‎ 解：因为是AB的垂直平分线，所以经过AB的中点，且垂直于向量。‎ 又AB中点，所以直线的法向式方程为。‎ 例3：已知三角形ABC的三个顶点坐标分别为，求：‎ ‎（1）BC边所在直线的方程；‎ ‎（2）BC边上的高AD所在直线的方程。‎ A B C D O 解：（1）BC边所在直线的一个方向向量，‎ 所以BC边所在直线的点方向式方程为 ‎。‎ ‎（2）高AD所在直线的一个法向量为，‎ 且经过点，所以高AD所在直线的点法向式方程为：。‎ 例4：已知直线经过点，且与直线垂直，求直线的方程。‎ 解：因为是直线的一个法向量。‎ 则是所求直线的一个方向向量，又所求直线过点，‎ 所以所求直线的点方向式方程为。‎ 例5：已知△ABC中，，点B、C的坐标分别为和。向量，且与AC边平行，求三角形三边所在直线的方程。‎ 解：因为B、C的坐标分别为和，则，所以BC边所在直线的点方向式方程为：；‎ 又AC与向量平行，所以AC边所在直线的点方向式方程为：；‎ 因为，所以向量是直线AB的法向量，则AB的点法向式方程为：。‎ 例6：已知直线经过点与轴、轴的正半轴分别交于点A、B，试求满足下列条件的直线的方程。‎ ‎（1）P是线段AB的中点；　　　（2）‎ ‎（3）最小；　　　（4）三角形OAB的面积最小； ‎ ‎ (5) 最小。‎ A B O 解：（1）设，因为是AB的中点，‎ 所以，即，所以，‎ 则的点方向方程为。‎ ‎（2）由得，‎ 即，所以，，所以此时直线方程为。‎ ‎（3）设，则所求直线的一个方向向量 ‎，则其方程为，即。‎ 又直线过点，所以，则，‎ ‎，当且时等号成立，此时。所求直线的方程为。‎ ‎（4），当且仅当时等号成立，此时，所求直线的方程为。‎ ‎11、2 直线的倾斜角与斜率 O M ‎1、直线倾斜角：‎ 设直线与轴相交于点M，将轴绕点M按逆时针方向旋转至直线重合时所成的最小正角叫做直线的倾斜角。当直线与轴平行或重合时，规定其倾斜角。‎ 直线的倾斜角也可以这样理解：直线向上方向与轴正方向的夹角。直线倾斜角的取值范围是。‎ ‎2、直线的斜率：‎ 当直线的倾斜角时，把叫做直线的斜率，用表示。即直线的斜率； ‎ 当时，直线的斜率不存在。‎ ‎3、直线倾斜角与斜率的变化关系：‎ ‎4、倾斜角、斜率与方向向量的关系：‎ 直线的倾斜角、斜率与方向向量都是对直线倾斜程度（即直线的方向）的刻画，因此它们之间可以互相转化。‎ O 直线的方向向量为，倾斜角为，斜率为。‎ ‎（1）若方向向量为，那么 当时，；‎ 当时，不存在，此时。‎ ‎（2）若直线的倾斜角为，那么 当时，，方向向量为；‎ 当时，其斜率不存在，方向向量可以为。‎ ‎（3）若直线的斜率为时，那么 其方向向量可以为；当时，，当时，。‎ ‎5、斜率公式：‎ ‎ 若直线经过点，则方向向量。‎ 当时，直线与轴垂直，此时直线的倾斜角为，斜率不存在；‎ 当时，直线的斜率。‎ ‎6、直线的点斜式方程：‎ 已知直线的斜率为，且通过点，求直线的方程。‎ 解：因为直线的方向向量为，又直线过点，当时，‎ 此直线的点方向式方程为，整理得：　　（1）‎ 当时，直线的方程为，满足（1）式。直线的方程为。‎ ‎ 方程称为直线的点斜式方程。‎ ‎7、直线的斜截式方程：‎ 已知直线的斜率为，且在轴上的截距为，求直线的方程。‎ 解：。‎ 例1：已知直线上的两点A、B，求直线的斜率与直线的倾斜角。‎ ‎（1）A（1,2），B（3,4）；　　 　　（2）A（－2,1），B（4,0）；‎ ‎（3）A（3,4），B（5,4）。 （4）， 。‎ 解：（1），倾斜角。‎ ‎（2），倾斜角。‎ ‎（3），倾斜角。‎ ‎（4），。‎ 例2：直线经过点，倾斜角的正弦值为，求直线的方程。‎ 解：设直线的倾斜角为，则，又，则，‎ 即其斜率或，‎ 所以所求的直线点斜式方程为或。‎ 例3：将直线绕其上面的一点按逆时针方向旋转后得到直线，求直线的方程。‎ 解：设直线的倾斜角为，则，的倾斜角为，‎ 所以。‎ 故的方程为。‎ 例4：已知直线经过点和点，求直线的斜率和倾斜角。‎ 解：当时，直线的斜率不存在，其倾斜角为；‎ 当时，直线的斜率为。‎ 若，即时，直线的倾斜角为；‎ 当，即时，直线的倾斜角为。‎ ‎8、复习直线方程的几种形式：‎ 点方向式：，其方向向量为（其中都不为零）；‎ 点法向式：，其法向量为；‎ 点斜式：，其中是直线的斜率；‎ 斜截式：。‎ 两点式：，直线经过点且与坐标轴不平行；‎ 截距式：，直线经过点，且都不为零。‎ ‎9、直线方程的一般形式：‎ 方程（不同时为零）称为直线的一般式方程。向量是它的一个法向量，向量是它的一个方向向量。‎ 例5：（1）求经过点且平行于直线的直线的方程。‎ ‎（2）求经过点且垂直于直线的直线的方程。‎ 解：（1）向量是所求直线的一个法向量，又直线过点，‎ 所求直线的点法向式方程为：，整理得：。‎ 解法二：设所求直线的方程为。又所求直线过点，‎ 代入得：，解得，所以所求直线方程为。‎ ‎（2）因为是直线的一个法向量，‎ 又与垂直，所以是直线的一个方向向量，‎ 又过点，所以的点方向式方程为，整理得：。‎ 例6：已知△ABC的顶点A（1,3），AB边上的中线所在的直线方程为，AC边上的高所在直线的方程为。求AC、AB、BC边所在直线的方程。‎ 解： AC与直线垂直，‎ 可设边AC所在直线方程为，‎ 又A点坐标为，所以，解得，‎ 所以边AC所在直线方程为：。‎ 设，则由B在AC边的高所在直线上，所以　　　（1）‎ 又AB中点在直线上，所以　　　（2）‎ 由（1）、（2）解得。即点，所以，‎ 则直线AB的点斜式方程为，整理得：。‎ ‎ 例7：求点关于直线对称点的坐标。‎ 解：设，则是直线的一个法向量，‎ 又的法向量是，所以，则　　　　　（1）‎ 又是线段AB的垂直平分线，所以AB中点在直线上，代入得：‎ ‎ 　　　　（2） 由（1）、（2）解得：，‎ 所以关于直线对称点的坐标为。‎ O A 例8：已知光线经过点，经轴反射后经过点，求入射光线与反射光线所在直线的方程。‎ 解法一：设反射点，因为入射角等于反射角，所以入射线MA的倾斜角与反射线AN的倾斜角互补，‎ 所以，则，解得，‎ 即反射点的坐标为，，‎ 所以入射线的方程为，即，‎ 反射线的斜率，所以反射线的方程为，即。‎ ‎ ‎ ‎ 解法二：关于轴的对称点，由光学原理知，‎ 所在直线即是入射线所在直线，，‎ 入射线的点斜式方程为，整理得：。‎ M点关于轴的对称点，同样求得反射线方程为。‎ 例9：求直线，关于直线对称的直线的方程。‎ O P 解：由过点，关于直线的对称点为，‎ 所以直线过点，又与交点，‎ 则也过，所以，所以的点斜式方程为，整理得：。‎ 例10：（1）已知直线过点，且与以，为端点的线段有公共点，求直线的斜率的取值范围。‎ ‎（2）已知两点，及直线，若直线与直线的交点位于线段的延长线上，求的取值范围。‎ 解：（1）两法，。‎ ‎（2）数形结合，。‎ 例11：设直线的方程为，倾斜角为。‎ ‎（1）试将表示为的函数；‎ ‎（2）若，求的取值范围；‎ ‎（3）若，求的取值范围。‎ 解：（1）‎ ‎（2）；‎ ‎（3）。‎ ‎11、3 两条直线的位置关系 ‎1、两条直线的交点 设两直线的方程分别为 ‎　　　　　　 （1）‎ ‎　　　　　　（2）‎ 若直线与有公共点，则点P的坐标必是方程组的解。‎ 反之，如果是方程组的解，那么以为坐标的点必是直线与直线的公共点。‎ ‎ 由此可知直线与的公共点的个数与方程组的解的个数相同。‎ ‎2、两条直线的相交、平行与重合 在同一平面上两条直线有相交、平行、重合三种不同的位置关系。‎ 对于方程组，‎ ‎ （1）当，即时，方程组有唯一解为。‎ ‎ 此时直线与相交于一点，交点坐标为。‎ ‎（2）当，或时，方程组没有解，‎ 此时直线没有公共点，即两直线平行；‎ ‎（3）当，且时，方程组有无数多组解，此时直线与重合。‎ 综上知：当时，两直线相交；当时，两直线平行或重合。‎ 例1：判断下列各组直线之间的位置关系，若相交，求出它们的交点坐标。‎ ‎（1）；‎ ‎（2）；‎ ‎（3）。‎ 解：（1）两直线相交，交点坐标为；‎ ‎　（2）两直线相交，交点坐标为；‎ ‎　（3）两直线平行。‎ 例2：讨论下列各组直线之间的位置关系：‎ ‎（1）；　　　　（2）。‎ 解：（1）当时，两直线相交；当或时，两直线平行；‎ ‎ 当时，两直线重合。‎ ‎（2）时两直线相交；且两直线平行；‎ ‎ 且时，两直线重合。‎ 例3：若三条直线不能构成三角形，求实数的值。‎ 解：三直线不能构成三角形，则至少有两条互相平行或三条直线过同一点。又与不平行。 ‎ ‎ （1）若，则，得；‎ ‎　 （2）若，则，得；‎ ‎　 （3）若三直线共点，由，解得交点坐标，‎ ‎ 代入方程得即。 ‎ ‎ 综上知：当或或时，三直线不能构成三角形。‎ ‎4、两条直线的夹角 平面上两直线相交构成四个角，它们是两对对顶角。把两直线相交所成的锐角或直角称为两直线的夹角，若两直线平行或重合，规定它们的夹角为0。因此直线夹角的取值范围是。‎ 夹角公式的推导：‎ 如果已知两条直线的方程分别为：（其中；不同时为零）。由与的方程可以知道：分别是直线与的方向向量，由图可以看出：‎ 由此可得两夹角公式为 ‎。‎ ‎5、两条直线的垂直 当两直线垂直时，，此时，则；反之若，则，它们的方向向量垂直，所以直线。‎ 因而两直线互相垂直的充要条件是。‎ 另一方面，设两直线的斜率分别为，则直线的方向向量分别为，，那么两直线的夹角公式可以为：‎ 当直线垂直时，则有。‎ 例4：已知两直线的方程分别为，求两直线的夹角。‎ 解： ，又，所以。‎ 例5：已知直线过点且与直线的夹角为，求直线的方程。‎ 解：设直线的斜率为，因为直线的斜率为，则 ，‎ 解得，直线方程为：；‎ 又当直线的斜率不存在，此时直线方程为：也满足题意。‎ 直线方程为：或。‎ 例6：已知等腰直角三角形ABC的直角顶点，斜边AB所在直线方程为，求两直角边所在直线的方程。‎ 解：设直角边所在直线的斜率为，因为斜边与直角边的夹角为，‎ 所以，解得：或，‎ 所以直角边所在直线的方程为与。‎ 例7：求直线的夹角平分线所在直线的方程。‎ 解：设直线的斜率为，由，根据夹角公式得：‎ ‎，解得：或。‎ 又直线的夹角为锐角或直角，‎ 所以与的夹角取值范围为，‎ 则根据夹角公式，所以。‎ 又由得的交点坐标为，所以直线的方程为。‎ 例8：等腰三角形两腰所在直线的方程分别为与，它的底边所在直线经过点，求底边所在直线的方程。‎ 解：由例7知底边所在直线的斜率为或，所以底边所在直线的方程为或。‎ 例9：已知三角形的两条高线方程为和，点是三角形的一个顶点。‎ ‎（1）求边所在直线的方程；‎ ‎（2）求三个内角的大小。‎ 解：点A不满足和。‎ 设是边AB上的高，则直线ABA B C O 的方向向量为，所以直线AB的方程为，‎ 设是边AC上的高，‎ 则直线AC的一个方向向量为，所以直线AC的方程为。‎ 由，得点B坐标为；‎ 由，得点C的坐标为。‎ 所以是直线BC的一个方向向量，‎ 则直线BC的点方向式方程为。‎ ‎（2），则是向量与的夹角，‎ ‎，所以；‎ ‎，则，所以，‎ 那么，。‎ 即三角形ABC的三个内角为：‎ ‎，，。‎ ‎11、4 点到直线的距离 ‎1、点到直线距离公式的推导：‎ 已知直线的方程是不同时为0），是直线外一点，求点P到直线的距离。‎ 方案一：由直线的方程是，知直线的法向量，‎ 所以过点P与直线垂直的直线的法向量为，则直线的方程为 设直线与的交点为，则坐标满足，‎ 方程组的解为，由两点间距离公式得：‎ ‎＝＝‎ ‎。所以点P到直线的距离为：‎ Q R O ‎。‎ 方案二：（构造直角三角形）如图：‎ 不妨直线与坐标轴不平行，点P在直线上的 射影为Q，过P作轴的平行线交直线于点R，‎ 则，又R点坐标，‎ 所以，‎ 由斜率公式知，所以，‎ 所以＝，‎ 即点P到直线的距离。‎ 当直线与坐标轴平行时，此式仍成立。‎ 方案三：向量法：‎ 如图：设为直线上任一点距离，直线的法向量，‎ 则＝。‎ 因为点在直线上，所以，即有：，‎ 代入得：，所以点P到直线距离为：。‎ 结论：直线外一点到直线的距离。‎ ‎2、两平行直线之间的距离：‎ 已知两平行直线，‎ 则这两平行直线之间的距离为：‎ ‎3、直线分平面区域问题 记，‎ ‎（1）当点与在直线同侧时，‎ 与同号；‎ ‎（2）当与在直线异侧时，‎ 与异号。‎ 例1：已知的三个顶点的坐标分别为。‎ ‎（1）求的面积； （2）求的角平分线所在直线的方程。‎ 解：（1），，到的距离，‎ ‎。‎ A B C O ‎（2）解法一：因为，‎ 设的平分线所在直线的斜率为，‎ 根据夹角公式得：‎ 解之得：或。又点B、C在角平分线的两侧，‎ 所以，即，则，‎ 所以，即所求的角平分的方程为。‎ 解法二：根据角平分线的性质，设的平分线与边BC交于点D，则 ‎，因为，即。所以，由定比分点知，D分BC成定比，根据定比分点公式：‎ ‎，所以，则方程为。‎ 即的平分线所在直线的方程为。‎ 例2：已知一正方形相对的两边所在直线的方程分别为：且坐标原点在此正方形的边上，求另外两边所在直线的方程。‎ 解：坐标原点不在直线上，则原点在与此两边垂直的直线上，过原点的直线斜率为，则此边所在直线的方程为。‎ 又正方形的边长相等，由两平行直线的距离知，正方形的边长为，‎ 设另一边方程为，那么，解得。‎ 故所求另外两边的直线方程为：‎ 与或与。‎ 例3：求过点且被两平行直线和所截线段长为 的直线的方程。‎ 解：两平行直线和之间的距离，‎ 所求直线被两平行直线截得的线段长为，所以所求直线与两平行直线的夹角为。‎ 设所求直线的斜率为，则所求直线方程为，由两直线的夹角公式：‎ ‎，解得：或，‎ 所以所求直线方程为：或。‎ 变化1：若将所截线段长变为，求此直线方程呢？‎ 解：由两平行间距离为，设所求直线与两平行线的夹角为，则，‎ 所以。则，解得：，‎ 则所求的直线方程为。‎ 又当直线的斜率不存在时，直线方程为，它与两平行直线的交点分别为，B、C两点间的距离为，所以直线也满足。‎ 故所求的直线方程为或。‎ 变化2：两条平行直线分别经过点。‎ ‎（1）求此两平行直线之间距离的取值范围；‎ ‎（2）若两平行直线之间的距离为，求此两直线的方程。‎ O A B C 解：（1）如图，设两平行直线之间的距离是，过点A作另一直线的垂线交于点C，则，‎ 所以，又两平行直线之间距离。‎ 故此两平行直线之间距离的取值范围为。‎ ‎（2）若两平行直线之间的距离等于，即，又，设所求直线与直线AB的夹角为，则，所以。而，设所求直线的斜率为，‎ 由夹角公式得：，解得，‎ 则所求直线方程为：与。‎ 又当直线的倾斜角为时，过A、B的两平行直线分别为与也满足题义。‎ 所以所求的直线方程为：与或与。‎ 例4：已知直线过点，且与以为端点的线段AB相交，求此直线斜率的取值范围。‎ 解：直线的方程：，又由题意知，可知点在直线的异侧或在直线上，因此：，‎ 即：，解得或。‎ 例5：求证：不论为何实数，直线恒过一个定点。‎ 证明：由得，‎ 所以直线过直线与的交点，由得。‎ 所以直线恒过定点。‎ 例6：直线：关于直线：对称的直线的方程。‎ 解：由题意可以知，直线过直线与的交点，且是与所成角的平分线，‎ 设直线方程为：，即，‎ 由两直线的夹角公式得：，‎ 解得。所以所求直线的方程为：。‎ 例7：已知直线与直线的交点在第一象限，求实数的取值范围。‎ 解法一：由直线，即，直线过点斜率为。‎ 直线在两坐标轴正半轴上的交点分别为。由题意知，直线与线段AB（不包括端点）相交。，所以直线的斜率满足：。‎ 解法二：对于直线，即，对于，，。由题意，A、B两点在直线的两侧，所以，‎ 即，所以。‎ 例8：求点到直线的距离的取值范围。‎ 解法一：由点到直线的距离公式：‎ ‎。‎ 当时，，当时，。‎ 所以点P到直线距离的取值范围是。‎ 解法二：由得，‎ 所以直线是过两直线与交点的直线，‎ 当在直线上时，，所以，又，所以，‎ 当时，等号成立，但，，所以不成立。‎ 故等号不成立，所以，综上知点P到直线距离的取值范围是。‎ 例9：已知线段AB与轴垂直，其长度为2，AB中点在射线上运动，为坐标原点，求的最大值。‎ 解：设的中点为，的倾斜角分别为，那么，，，则＝。‎ 当时等号成立。当时，此时，当时，此时。所以的最大值为。‎ 例10：已知两直线与，在此两直线的上方有一点P，且P点到的距离分别为和。过点P分别作与的垂线，垂足分别为A、B。求：‎ ‎（1）点P的坐标；‎ ‎（2）线段AB的长；‎ ‎（3）四边形OAPB的面积（O是坐标原点）。‎ A B O P 解：（1）设与直线距离为的直线为，则方程可设为，由两平行线之间的距离公式：，得，‎ 因为P在直线的上方，所以直线的方程为。‎ 设与直线距离为的直线为，因为，则可设为。‎ 由两平行线间的距离公式：，则，因为点P在直线上方，‎ 所以，得直线方程：。‎ 由，得点P的坐标为。‎ ‎（2）由PA与直线垂直，所以得直线PA方程为：；‎ 又直线PB与直线垂直，得直线PB方程为：。‎ 由，解得：，由解得：，‎ 所以。‎ ‎（3）。‎