2010中考数学台湾考试试题

2010中考数学台湾考试试题

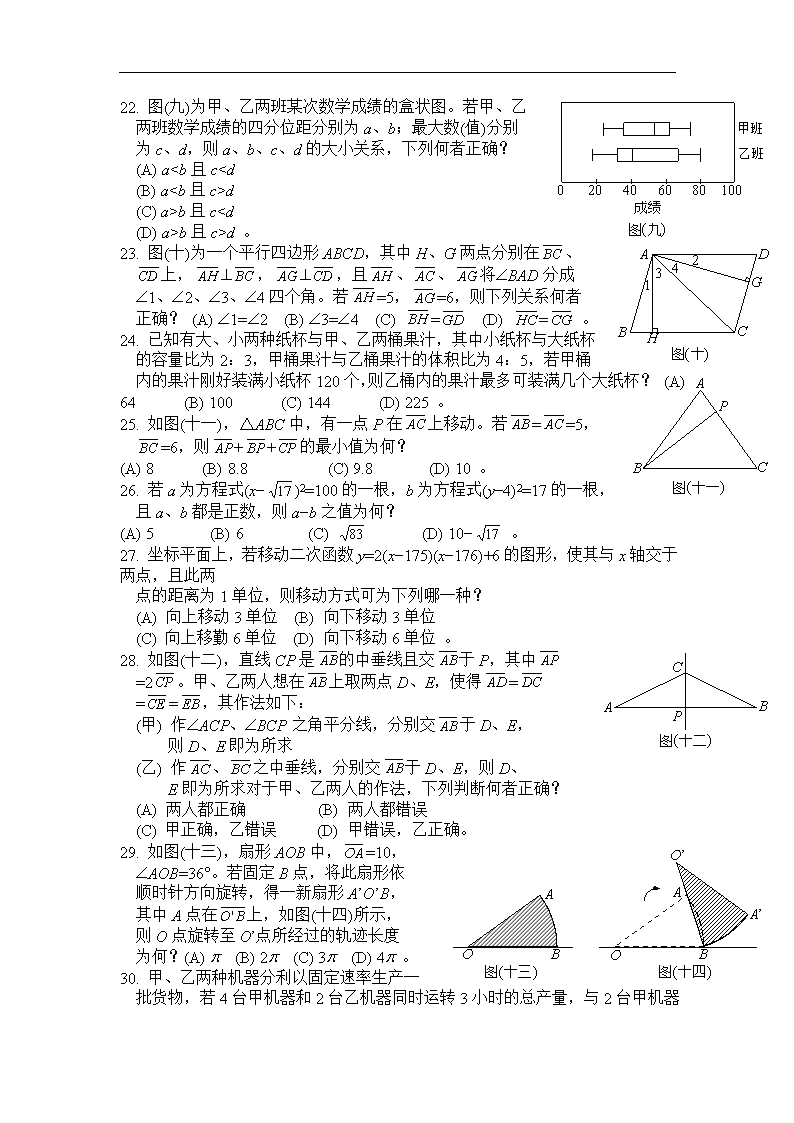
‎2010年 台湾 第一次国民中学学生基本学力测验(台湾中考)数学科题本 ‎1. 下列何者是0.000815的科学记号？ ‎ ‎(A) 8.15´10-3 (B) 8.15´10-4 (C) 815´10-3 (D) 815´10-6 。‎ ‎2. 小芬买15份礼物，共花了900元，已知每份礼物内鄱有1包饼干及每支售价20元的棒棒糖A B C D E F G H 图(一)‎ 2支，若每包饼干的售价为x元，则依题意可列出下列哪一个一元一次方程式？ (A) 15(2x+20)=900 (B) 15x+20´2=900 ‎ ‎(C) 15(x+20´2)=900 (D) 15´x´2+20=900 。 3. 下列选项中，哪一段时间最长？ ‎ ‎(A) 15分 (B) 小时 (C) 0.3小时 (D) 1020秒。 4. 图(一)表示D、E、F、G四点在△ABC三边上的位置，其中与 ‎ 交于H点。若ÐABC=ÐEFC=70°，ÐACB=60°，ÐDGB=40°，则下列哪 ‎ 一组三角形相似？‎ ‎(A) △BDG，△CEF (B) △ABC，△CEF ‎ (C) △ABC，△BDG (D) △FGH，△ABC 。 5. 计算 | -1-(-) |-| -- | 之值为何？ ‎ ‎(A) - (B) - (C) (D) 。‎ ‎6. 下列何者为5x2+17x-12的因式？ (A) x+1 (B) x-1 (C) x+4 (D) x-4 。‎ ‎7. 计算106´(102)3¸104之值为何？(A) 108 (B) 109 (C) 1010 (D) 1012。 A B C D E O 图(二)‎ 8. 如图(二)，为圆O的直径，C、D两点均在圆上，其中与交于 ‎ E点，且^。若=4，=2，则长度为何？‎ ‎ (A) 6 (B) 7 (C) 8 (D) 9 。‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎1‎ 圖(三)‎ ‎9. 有数颗等重的糖果和数个大、小砝 ‎ 码，其中大砝码皆为‎5克、大砝码 ‎ 皆为‎1克，且图(三)是将糖果与砝码 ‎ 放在等臂天平上的两种情形。判断 ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎1‎ ‎1‎ ‎5‎ ‎5‎ ‎5‎ ‎5‎ ‎1‎ ‎(A)‎ ‎5‎ ‎1‎ ‎5‎ ‎1‎ ‎1‎ ‎(B)‎ ‎(C)‎ ‎(D)‎ ‎ 下列哪一种情形是正确的？ ‎ ‎10. 下列四个选项中的数列，哪一个不是等差数列？ (A) ，，，， (B) ，，，，‎ ‎ (C) ，2，3，4，5 (D) ，2，3，4，5 。‎ A C B D 图(四)‎ ‎11. 坐标平面上有一函数y=24x2-48的图形，其顶点坐标为何？ (A) (0，-2) (B) (1，-24) (C) (0，-48) (D) (2，48) 。 ‎ ‎12. 解二元一次联立方程式，得y=？ ‎ ‎(A) - (B) - (C) - (D) -。 13. 图(四)为△ABC和一圆的重迭情形，此圆与直线BC相切于C点，‎ ‎ 且与交于另一点D。若ÐA=70°，ÐB=60°，则 的度数为何？ (A) 50 (B) 60 (C) 100 (D) 120 。‎ ‎14. 以下有甲、乙、丙、丁四组资料 甲：13，15，11，12，15，11，15 乙：6，9，8，7，9，9，8，5，4 丙：5，4，5，7，1，7，8，7，4 丁：17，11，10，9，5，4，4，3 判断哪一组资料的全距最小？ ‎ ‎(A) 甲 (B) 乙 (C) 丙 (D) 丁 。‎ ‎15. 坐标半面上，在第二象限内有一点P，且P点到x轴的距离是4，到y轴的距离是5，则P ‎ 点坐标为何？ ‎ ‎(A) (-5，4) (B) (-4，5) (C) (4，5) (D) (5，-4) 。‎ ‎16. 计算+之值为何？ ‎ ‎(A) 2 (B) 3 (C) 4 (D) 5。‎ ‎17. 已知有一多项式与(2x2+5x-2)的和为(2x2+5x+4)，求此多项式为何？‎ A B C O a b c ‎0‎ -1‎ ‎1‎ 图(五)‎ ‎ (A) 2 (B) 6 (C) 10x+6 (D) 4x2+10x+2 。 18. 图(五)数在线的A、B、C三点所表示的数分别为 ‎ a、b、c。根据图中各点位置，判断下列各式何者 ‎ 正确？ ‎ ‎(A) (a-1)(b-1)>0 (B) (b-1)(c-1)>0‎ ‎ (C) (a+1)(b+1)<0 (D) (b+1)(c+1)<0 。‎ ‎19. 自连续正整数10~99中选出一个数，其中每个数被选出的机会相等。求选出的数其十位数 图(六)‎ 图(七)‎ 图(八)‎ ‎ 字与个位数字的和为9的机率为何？ ‎ ‎(A) (B) (C) (D) 。 20. 将图(六)的正方形色纸沿其中一条 对角线对折后，再沿原正方形的另 ‎ 一条对角线对折，如图(七)所示。 最后将图(七)的色纸剪下一纸片， 如图(八)所示。若下列有一图形 为图(八)的展开图，则此图为何？‎ ‎(A)‎ ‎(B)‎ ‎(C)‎ ‎(D)‎ ‎21. 已知456456=‎23´a´7´11´13´b，其中a、b均为质数。若b>a，则b-a之值为何？ (A) 12 (B) 14 (C) 16 (D) 18 。‎ ‎0‎ ‎20‎ ‎40‎ ‎60‎ ‎80‎ ‎100‎ 甲班 乙班 成绩班 图(九)‎ ‎22. 图(九)为甲、乙两班某次数学成绩的盒状图。若甲、乙 ‎ 两班数学成绩的四分位距分别为a、b；最大数(值)分别 ‎ 为c、d，则a、b、c、d的大小关系，下列何者正确？ (A) ad (C) a>b且cb且c>d 。‎ A B C D G H ‎1‎ ‎2‎ ‎3‎ ‎4‎ 图(十)‎ ‎23. 图(十)为一个平行四边形ABCD，其中H、G两点分别在、‎ ‎ 上，^，^，且、、将ÐBAD分成 ‎ Ð1、Ð2、Ð3、Ð4四个角。若=5，=6，则下列关系何者 ‎ 正确？ (A) Ð1=Ð2 (B) Ð3=Ð4 (C) = (D) = 。‎ ‎24. 已知有大、小两种纸杯与甲、乙两桶果汁，其中小纸杯与大纸杯 ‎ 的容量比为2：3，甲桶果汁与乙桶果汁的体积比为4：5，若甲桶 ‎ 内的果汁刚好装满小纸杯120个，则乙桶内的果汁最多可装满几个大纸杯？ (A) 64 (B) 100A B C P 图(十一)‎ (C) 144 (D) 225 。 25. 如图(十一)，△ABC中，有一点P在上移动。若==5，‎ ‎ =6，则++的最小值为何？‎ ‎(A) 8 (B) 8.8 (C) 9.8 (D) 10 。‎ ‎26. 若a为方程式(x-)2=100的一根，b为方程式(y-4)2=17的一根，‎ ‎ 且a、b都是正数，则a-b之值为何？ ‎ ‎(A) 5 (B) 6 (C) (D) 10- 。 27. 坐标平面上，若移动二次函数y=2(x-175)(x-176)+6的图形，使其与x轴交于两点，且此两 ‎ 点的距离为1单位，则移动方式可为下列哪一种？ (A) 向上移动3单位 (B) 向下移动3单位 ‎ ‎(C) 向上移勤6单位 (D) 向下移动6单位 。‎ A B C P 图(十二)‎ ‎28. 如图(十二)，直线CP是的中垂线且交于P，其中 ‎ =2。甲、乙两人想在上取两点D、E，使得=‎ ‎ ==，其作法如下： (甲) 作ÐACP、ÐBCP之角平分线，分别交于D、E，‎ ‎ 则D、E即为所求 (乙) 作、之中垂线，分别交于D、E，则D、‎ ‎ E即为所求对于甲、乙两人的作法，下列判断何者正确？ (A) 两人都正确 (B) 两人都错误 ‎ ‎(C) 甲正确，乙错误 (D) 甲错误，乙正确。‎ A B O A B O A’‎ O’‎ 图(十三)‎ 图(十四)‎ ‎29. 如图(十三)，扇形AOB中，=10，‎ ‎ ÐAOB=36°。若固定B点，将此扇形依 ‎ 顺时针方向旋转，得一新扇形A’O’B，‎ ‎ 其中A点在上，如图(十四)所示，‎ ‎ 则O点旋转至O’点所经过的轨迹长度 ‎ 为何？(A) p (B) 2p (C) 3p (D) 4p 。‎ ‎30. 甲、乙两种机器分利以固定速率生产一 ‎ 批货物，若4台甲机器和2台乙机器同时运转3小时的总产量，与2‎ 台甲机器和5台乙机器 ‎ 同时运转2小时的总产量相同，则1台甲机器运转1小时的产量，与1台乙机器运转几小时 ‎ 的产量相同？ ‎ ‎(A) (B) (C) (D) 2 。‎ D C B A E F P 图(十五)‎ ‎31. 如图(十五)梯形ABCD的两底长为=6，=10，中线为，‎ ‎ 且ÐB=90°，若P为上的一点，且将梯形ABCD分成面积相 ‎ 同的两区域，则△EFP与梯形ABCD的面积比为何？ (A) 1：6 (B) 1：10 (C) 1：12 (D) 1：16 。‎ B A C D E F G H 图(十六)‎ ‎32. 如图(十六)，有一圆内接正八边形ABCDEFGH，若△ADE的面积为 ‎ 10，则正八边形ABCDEFGH的面积为何？‎ ‎ (A) 40 (B) 50 (C) 60 (D) 80 。‎ ‎33. 如图(十七)，在同一直在线，甲自A点开始追赶等速度前进的乙，‎ ‎ 且图(十八)长示两人距离与所经时间的线型关系。若乙的速率为每秒 甲 乙 A ‎9公尺甲 图(十七)‎ 時間(秒)‎ ‎0‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ 图(十八)‎ ‎3‎ ‎6‎ ‎9‎ 甲 與 乙 距 離 公尺 ‎(‎ ‎)‎ ‎0‎ ‎ 1.5公尺，则经过40秒，甲自A点移动多少公尺？ (A) 60‎ ‎ (B) 61.8‎ ‎ (C) 67.2‎ ‎ (D) 69 。 ‎ ‎3‎ ‎2‎ ‎4‎ ‎6‎ 图(十九)‎ ‎34. 如图(十九)，用四个螺丝将四条不可弯曲的木条围成一个木框，不计 ‎ 螺丝大小，其中相邻两螺丝的距离依序为2、3、4、6，且相邻两木条 ‎ 的夹角均可调整。若调整木条的夹角时不破坏此木框，则任两螺丝的 ‎ 距离之最大值为何？ ‎ ‎(A) 5 (B) 6 (C) 7 (D) 10 。‎ 参考答案：‎ ‎1. B , 2. C , 3. B , 4. B , 5. A , 6. C , 7. A , 8. C , 9. D , 10. D , 11. C , 12. D , 13. C , 14. A , 15. A , ‎ ‎16. B, 17. B , 18. D , 19. B , 20. B , 21. C , 22. A , 23. A , 24. B , 25. C , 26. B , 27. D , 28. D , 29. D , 30. A , 31. D , 32. A , 33. C , 34. C ,‎