- 2021-04-16 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考复习专题——切线的证明方法
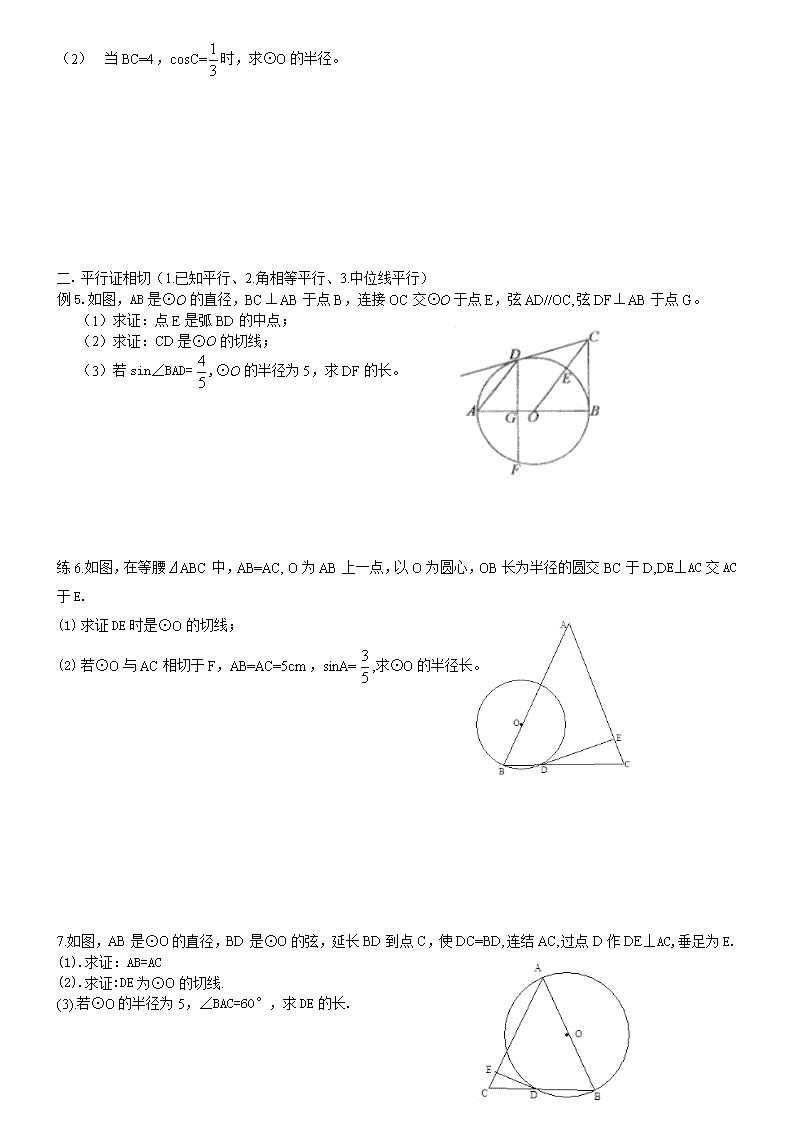
切线的证法 1. 直线与圆只有唯一公共点,则直线是圆的切线 2. 圆心到直线的距离等于圆的半径,则直线是圆的切线 3. 经过半径的外端,且垂直于这条半径的直线是圆的切线 一. 角平分线证相切:(作弦心距,利用勾股定理) 例:.如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F. (1)求证:DE是⊙O的切线; (2)若=,求的值。 练习2.如图,AB为⊙O的直径,C为⊙O上一点,∠BAC的平分线交⊙O于点D,过D点作EF∥BC交AB的延长线于点E,交AC的延长线于点F。 (1)求证:EF为⊙O的切线; (2)若sin∠ABC=,CF=1,求⊙O的半径及EF的长。 3. 如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F. (1)求证:DE是⊙O的切线; (2)若DE=3,⊙O的半径为5,求BF的长. 4.已知如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径. (1) 求证:AE与⊙O相切; (1) 当BC=4,cosC=时,求⊙O的半径。 一. 平行证相切(1.已知平行、2.角相等平行、3.中位线平行) 例5.如图,AB是⊙O的直径,BCAB于点B,连接OC交⊙O于点E,弦AD//OC,弦DFAB于点G。 (1)求证:点E是弧BD的中点; (2)求证:CD是⊙O的切线; (3)若sin∠BAD=,⊙O的半径为5,求DF的长。 练6.如图,在等腰⊿ABC中,AB=AC,O为AB上一点,以O为圆心,OB长为半径的圆交BC于D,DE⊥AC交AC于E. (1) 求证DE时是⊙O的切线; (2) 若⊙O与AC相切于F,AB=AC=5cm,sinA=,求⊙O的半径长。 7.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E. (1).求证:AB=AC (2).求证:DE为⊙O的切线. (3).若⊙O的半径为5,∠BAC=60°,求DE的长. 8.如图 ,矩形中,.点是上的动点,以为直径的与交于点,过点作于点. (1)当是的中点时: ①的值为______________; ② 证明:是的切线; (2)试探究:能否与相切?若能,求出此时的长;若不能,请说明理由. D E O C B G F A 9.如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结OG并延长与BE相交于点F,延长AF与CB的延长线相交于点P. (1)求证:BF=EF; (2)求证:PA是⊙O的切线; (3)若FG=BF,且⊙O的半径长为3, 求BD和FG的长度. 一. 角度转化证切线(中线证直角、角度转化证直角) 例10.已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=OB. (1)求证:AB是⊙O的切线; (2)若∠ACD=45°,OC=2,求弦AD、CD的长. 11..如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO. (1).求证BD是⊙O的切线。 (2).若点E是劣弧BC上一点,AE与BC相交于点F,且⊿BEF的面积为8,cos∠BFA=,求⊿ACF的面积。 12.如图,△ABC内接于半圆,AB是直径,过A作直线MN,若∠MAC=∠ABC. (1).求证:MN是半圆的切线 (2).设D是弧AC的中点,连结BD交AC于G,过D作DE⊥AB于E,交AC于F.求证:FD=FG (3).若△DFG的面积为4.5,且DG=5,GC=4.试求△BCG的面积 13. 如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于E,交AB于H,交AC于F.P是ED延长线上一点且PC=PF. (1) 求证:PC是⊙O的切线; (2) 点D在劣弧AC什么位置时,才能使,为什么? (3) 在(2)的条件下,若OH=1,AH=2,求弦AC的长. 14.如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC. (1)求证:AC2=AE·AB; (2)延长EC到点P,连结PB,若PB=PE, 试判断PB与⊙O的位置关系,并说明理由. 15.如图所示,AB是半圆O的直径,C是半径OA上的一点,PC⊥AB,点D是半圆上位于PC右侧的一点,连接AD交线段PC于点E,且PD=PE. (1) 求证:PD是⊙O的切线; (2) 若⊙O的半径为4,PC=8,设OC=x,PD=y. ① 求y关于x的函数关系式 ② 当x=1时,求tan∠BAD的值. 16.如图,已知是的直径,点在上,过点的直线与的延长线交于点,,. O N B P C A M (1)求证:是的切线; (2)求证:; (3)点是弧AB的中点,交于点, 若,求MN×MC的值. 17.如图,扇形 OAB的半径OA=r,圆心角∠AOB=90°,点C是弧上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点M在DE上,DM=2EM,过点C的直线PC交OA的延长线于点P,且∠CPO=∠CDE. (1)求证:DM=r; (2)求证:直线PC是扇形OAB所在圆的切线; (3)设y=CD+3CM,当∠CPO=60°时,请求出y关于r的函数关系式。查看更多