- 2021-04-16 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年江苏省常州市“教学研究合作联盟”高二下学期期中考试数学(理)试题 Word版
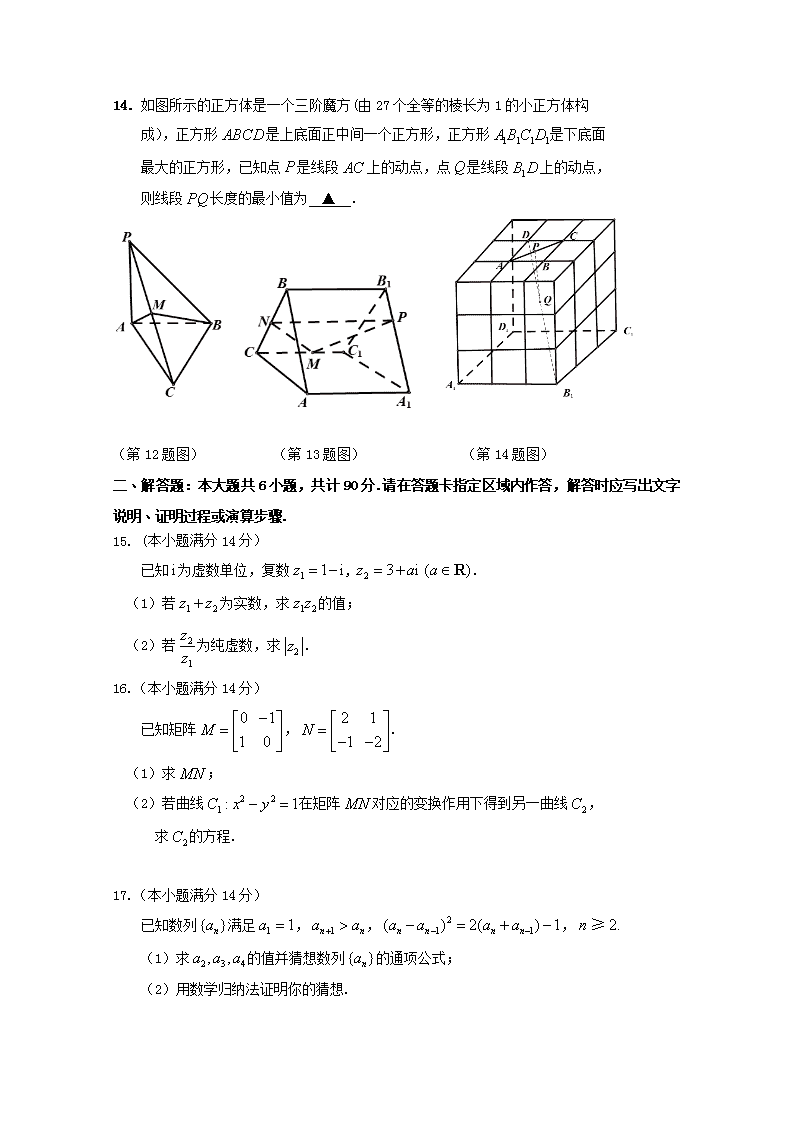
江苏省常州市“教学研究合作联盟” 2018-2019学年高二下学期期中考试数学(理科)试题 注意事项 1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分。本试卷满分160分,考试时间120分钟。 2.答题前,请务必将自己的姓名、考试号用毫米黑色签字笔填写在答题卡指定位置。 3.答题时,必须用毫米黑色签字笔填写在答题卡的指定位置,在其它位置作答一律无效。 4.如有作图需要,可用2B铅笔作答,并加黑加粗,描写清楚。 5. 请保持答题卡卡面清洁,不要折叠、破损。一律不准使用胶带纸、修正液及可擦写的圆珠笔。 一﹑填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上. 1.若复数满足(为虚数单位),则复数的实部是 ▲ . 2.已知,是空间两个单位向量,它们的夹角为,那么 ▲ . 3.若复数满足其中为虚数单位,为的共轭复数,则在复 平面内对应的点位于第 ▲ 象限. 4.设,是两个不共线的空间向量,若,, ,且三点共线,则实数的值为 ▲ . 5.若向量,,且与的夹角为钝角,则实数的取 值范围为 ▲ . 6.著名的哥德巴赫猜想指出:“任何大于的偶数可以表示为两个素数的和”, 用反证法研究该猜想,应假设的内容是 ▲ . 7.如图,在正四面体中,分别为的中点,是线段 上一点,且,若,则的值为 ▲ . 8.我们知道等比数列与等差数列在许多地方都有类似的性质,请由等差数列 的前项和公式.类比得到正项等比数列的前项 积公式 ▲ . 9.用数学归纳法证明等式:,则从到 时左边应添加的项为 ▲ . 10.如图,在直三棱柱中,,, 点是棱上一点,且异面直线与所成角的余弦值为,则 的长为 ▲ . 11.德国数学家莱布尼兹发现了如图所示的单位分数三角形(单位分数是指分子 为﹑分母为正整数的分数),称为莱布尼兹三角形.根据前行的规律,第 行的左起第个数为 ▲ . (第7题图) (第10题图) (第11题图) 12.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的三棱锥称 之为鳖臑(bie nao).已知在鳖臑中,平面, ,为的中点,则点到平面的距离为 ▲ . 13. 如图,已知正三棱柱中,,分别为 的中点,点在直线上且满足若平面 与平面所成的二面角的平面角的大小为,则实数的值为 ▲ . 14. 如图所示的正方体是一个三阶魔方(由27个全等的棱长为1的小正方体构 成),正方形是上底面正中间一个正方形,正方形是下底面 最大的正方形,已知点是线段上的动点,点是线段上的动点, 则线段长度的最小值为 ▲ . (第12题图) (第13题图) (第14题图) 二﹑解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明﹑证明过程或演算步骤. 15. (本小题满分14分) 已知为虚数单位,复数,. (1) 若为实数,求的值; (2) 若为纯虚数,求. 16.(本小题满分14分) 已知矩阵 , . (1)求; (2)若曲线在矩阵对应的变换作用下得到另一曲线, 求的方程. 17.(本小题满分14分) 已知数列满足,,, (1)求的值并猜想数列的通项公式; (2)用数学归纳法证明你的猜想. 18.(本小题满分16分) 如图,在四棱锥中,已知平面,且四边形为 直角梯形,,,点,分 别是,的中点. (1)求证:平面; (2)若点为棱上一点,且平面平面, 求证: 19.(本小题满分16分) 如图,在正三棱柱中,所有棱长都等于. (1)当点是的中点时, ①求异面直线和所成角的余弦值; ②求二面角的正弦值; (2)当点在线段上(包括两个端点)运动时,求直线与 平面所成角的正弦值的取值范围. (第18题图) (第19题图) 20.(本小题满分16分) (1)是否存在实数,,,使得等式 对于一切正整数都成立?若存在, 求出,,的值并给出证明;若不存在,请说明理由. (2)求证:对任意的,. 常州市“教学研究合作联盟” 2018学年度第二学期期中质量调研 高二 数学(理科)参考答案和评分标准 一﹑填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上. 1. 1 2. 3.四 4. 4或-1 5. 且 6. 存在一个大于2的偶数不可以表示为两个素数的和. 7. 8. 9. 10. 1 11. 12. 13. 14. 二﹑解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明﹑证明过程或演算步骤. 15.解:(1)因为,若为实数,则. ……… 3分 此时,所以 ……… 7分 (2)因为, ……… 10分 若为纯虚数,则,得,……… 12分 所以 ……… 14分 16.解:(1) = ……… 6分 (2)设曲线上任一点坐标为在矩阵对应的变换作用下得到点则 =,即,解得.……… 10分 因为所以整理得,所以的方程为……… 14分 17.解:(1)由① 得解得或 又所以 将代入①,可得或 又所以 将代入①,可得或 又所以……… 3分 故猜想数列的通项公式为……… 5分 (2) ①当时,,猜想成立. ②假设当时,猜想成立,即……… 7分 则当时,由①得 即 即 即 即 即 解得或……… 12分 又所以故当时,猜想成立. 综上:由①②得.……… 14分 18.解:平面,平面 平面,平面 又因为所以,则两两 垂直,则以为正交基底, 建立如图所示的空间直角坐标系 则各点的坐标为 因为点分别是,的中点,所以 ……… 2分 (1)证明:设平面的一个法向量为 因为 由 得,令所以 则……… 5分 因为所以 又平面所以平面.……… 8分 (注:平面没交代扣1分,如果不用空间向量的方法做,比如取的中点证明平面平面,或者延长和相交于点然后证明也可以,但如果推理过程有一步错,则扣6分) (2)证明:因为为棱上一点,所以 设则,所以 即所以 设平面的一个法向量为则 所以消去可得 令则所以……… 12分 平面平面则所以…… 14分 从而因为所以 则即……… 16分 19. 解:(1)取的中点为建立如图所示的空间直角坐标系,则 当是的中点时,则 ① 设异面直线和所成角为则 = ……… 4分 ②设平面的一个法向量为则 所以令则… 5分 设平面的一个法向量为则 令……… 6分 设二面角的平面角为, 则……… 8分 所以……… 9分 (2)当在上运动时,设 设 则 设直线与平面所成的角为则 ……… 11分 设设所以 设 直线与平面所成的角的正弦值的取值范围为 ……… 16分 19. 解:(1)在等式中 令得①;令得②; 令得③;由①②③解得 对于都有 成立. ……… 3分 下面用数学归纳法证明:对一切正整数,式都成立. ①当时,由上所述知式成立; ②假设当时式成立,即 , 那么当时, ……… 5分 综上:由①②得对一切正整数,式都成立,所以存在时题设的等 式对于一切正整数都成立.……… 8分 (2) 证明: ①当时,左式,右式,所以左式<右式,则时不等式成立; ②假设当时不等式成立,即 , 那么当时, ……… 10分 下面证明当时,. 设,则所以在 上单调增,所以即时,. 因为,所以则 ……… 12分 因为 所以 由得 那么时不等式也成立. 综上:由①②可得对任意. ……… 16分查看更多