【物理】2020届一轮复习人教版磁场课时作业

【物理】2020届一轮复习人教版磁场课时作业

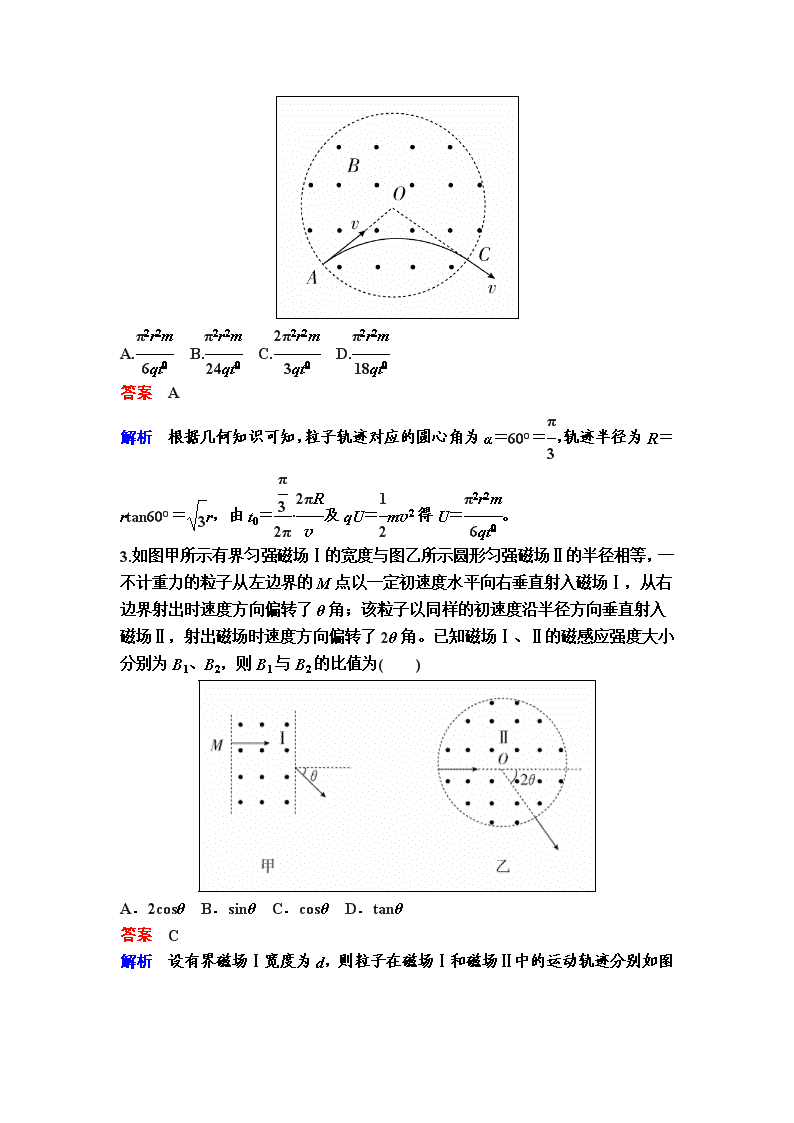
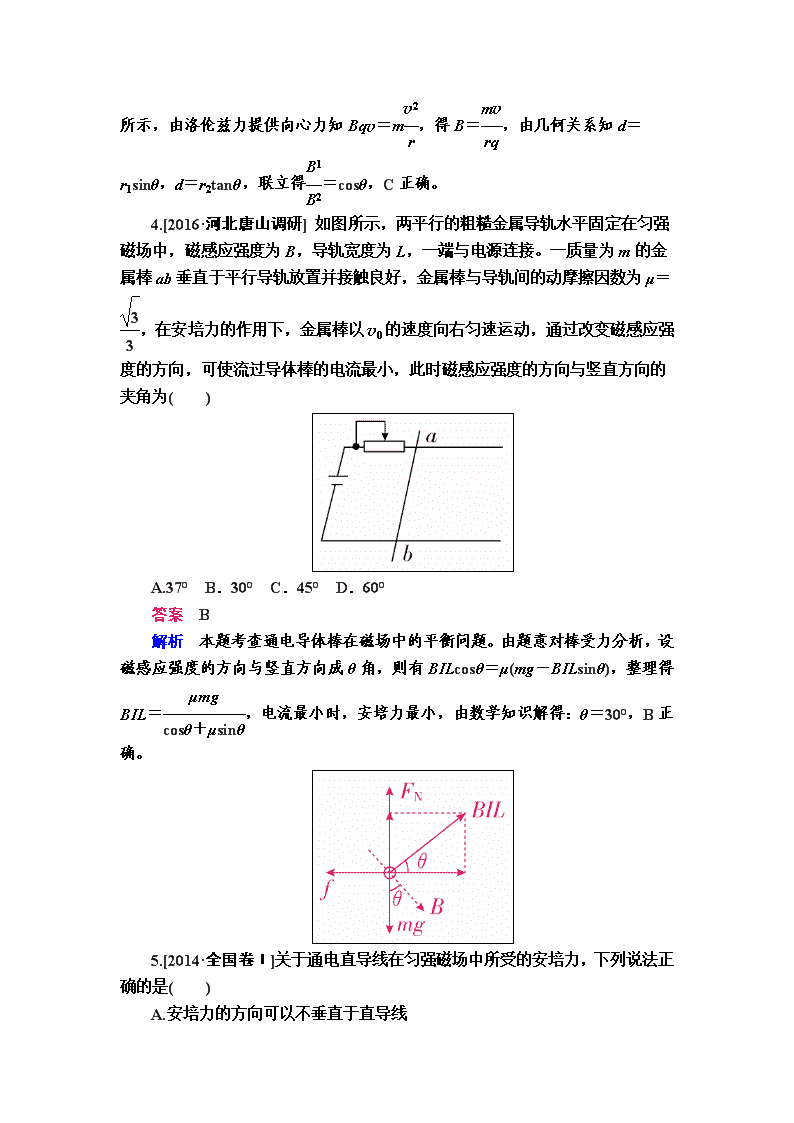
‎2020届一轮复习人教版 磁场 课时作业 一、选择题(本题共10小题，每小题6分，共60分。其中1～5为单选，6～10为多选)‎ ‎1. [2017·甘肃省一模]如图所示，两相邻且范围足够大的匀强磁场区域Ⅰ和Ⅱ的磁感应强度方向平行，大小分别为B和2B。一带正电粒子(不计重力)以速度v从磁场分界线MN上某处射入磁场区域Ⅰ，其速度方向与磁场方向垂直且与分界线MN成60°角，经过t1时间后粒子进入到磁场区域Ⅱ，又经过t2时间后回到区域Ⅰ，设粒子在区域Ⅰ、Ⅱ中的角速度分别为ω1、ω2，则(　　)‎ A.ω1∶ω2＝1∶1 B．ω1∶ω2＝2∶1‎ C.t1∶t2＝1∶1 D．t1∶t2＝2∶1‎ 答案　C 解析　由qvB＝m和v＝ωR得ω＝，故ω1∶ω2＝1∶2；粒子在Ⅰ中的轨迹对应的圆心角均为120°，在Ⅱ中的轨迹对应的圆心角为240°由T＝ T2＝和t＝·T知t1∶t2＝1∶1。‎ ‎2. [2017·四川四市二诊]如图所示，半径为r的圆形空间内，存在垂直于纸面向外的匀强磁场，一个质量为m，电荷量为q的带电粒子(不计重力)，从静止经电场加速后从圆形空间边缘上的A点沿半径方向垂直于磁场方向射入磁场，在C点射出，已知∠AOC＝120°，粒子在磁场中运动时间为t0，则加速电场的电压是(　　)‎ A. B. C. D. 答案　A 解析　根据几何知识可知，粒子轨迹对应的圆心角为α＝60°＝，轨迹半径为R＝rtan60°＝r，由t0＝·及qU＝mv2得U＝。‎ ‎3.如图甲所示有界匀强磁场Ⅰ的宽度与图乙所示圆形匀强磁场Ⅱ的半径相等，一不计重力的粒子从左边界的M点以一定初速度水平向右垂直射入磁场Ⅰ，从右边界射出时速度方向偏转了θ角；该粒子以同样的初速度沿半径方向垂直射入磁场Ⅱ，射出磁场时速度方向偏转了2θ角。已知磁场Ⅰ、Ⅱ的磁感应强度大小分别为B1、B2，则B1与B2的比值为(　　)‎ A．2cosθ B．sinθ C．cosθ D．tanθ 答案　C 解析　设有界磁场Ⅰ宽度为d，则粒子在磁场Ⅰ和磁场Ⅱ中的运动轨迹分别如图所示，由洛伦兹力提供向心力知Bqv＝m，得B＝，由几何关系知d＝r1‎ sinθ，d＝r2tanθ，联立得＝cosθ，C正确。‎ ‎4.[2016·河北唐山调研] 如图所示，两平行的粗糙金属导轨水平固定在匀强磁场中，磁感应强度为B，导轨宽度为L，一端与电源连接。一质量为m的金属棒ab垂直于平行导轨放置并接触良好，金属棒与导轨间的动摩擦因数为μ＝，在安培力的作用下，金属棒以v0的速度向右匀速运动，通过改变磁感应强度的方向，可使流过导体棒的电流最小，此时磁感应强度的方向与竖直方向的夹角为(　　)‎ A.37° B．30° C．45° D．60°‎ 答案　B 解析　本题考查通电导体棒在磁场中的平衡问题。由题意对棒受力分析，设磁感应强度的方向与竖直方向成θ角，则有BILcosθ＝μ(mg－BILsinθ)，整理得BIL＝，电流最小时，安培力最小，由数学知识解得：θ＝30°，B正确。‎ ‎5.[2014·全国卷Ⅰ]关于通电直导线在匀强磁场中所受的安培力，下列说法正确的是(　　)‎ A.安培力的方向可以不垂直于直导线 B.安培力的方向总是垂直于磁场的方向 C.安培力的大小与通电直导线和磁场方向的夹角无关 D.将直导线从中点折成直角，安培力的大小一定变为原来的一半 答案　B 解析　安培力的方向、磁感应强度的方向及电流的方向遵循左手定则，所以安培力的方向既垂直于直导线，也垂直于磁场的方向，B正确，A错误；当通电直导线与磁场方向垂直时，安培力最大F＝BIl，当通电直导线与磁场方向平行时，安培力最小为零，C错误；由于通电直导线与磁场方向夹角不确定，将直导线从中点折成直角，直导线在磁场中的有效长度不一定变为原来的，安培力的大小不一定变为原来的一半，D错误。‎ ‎6. [2017·山东临汾市二模]如图所示，无限长水平直导线中通有向右的恒定电流I，导线正上方沿竖直方向有一用绝缘细线悬挂着的正方形线框。线框中通有沿逆时针方向的恒定电流I，线框的边长为L，线框下边与直导线平行，且到直导线的距离也为L。已知在长直导线的磁场中距长直导线r处的磁感应强度大小为B＝k(k为常量)，线框的质量为m，则剪断细线的瞬间，线框的加速度为(　　)‎ A.0 B.＋g C.－g D.＋g 答案　D 解析　线框下边受到的安培力的大小为F1＝k·IL＝kI2，方向向下。线框上边受到的安培力大小F2＝·IL＝kI2，方向向上。根据牛顿第二定律可得，F1＋mg－F2＝ma，解得：a＝＋g，D正确。‎ ‎7.(2017·安徽六校教育研究会第一次联考)如图所示,在x轴上方存在垂直于纸面向里的磁感应强度为B的匀强磁场,x 轴下方存在垂直于纸面向外的磁感应强度为的匀强磁场。一带负电的粒子质量为m,电荷量为q,从原点O与x轴成θ=30°斜向上射入磁场,且在x轴上方运动半径为r(不计重力),则(　　)‎ A.粒子经偏转一定能回到原点O B.粒子完成一次周期性运动的时间为 C.粒子在x轴上方和下方两磁场中运动的半径之比为1∶2‎ D.粒子第二次射入x轴上方磁场时,沿x轴方向前进了3r 答案BCD 解析根据左手定则判断可知,粒子在第一象限沿顺时针方向运动,而在第四象限沿逆时针方向运动,故不可能回到原点O,故A错误。因第四象限中磁感应强度为第一象限中的一半,故第四象限中的轨迹半径为第一象限中轨迹半径的2倍,如图所示,由几何关系可知,负电荷在第一象限轨迹所对应的圆心角为60°,在第四象限轨迹所对应的圆心角也为60°,在一个周期内,粒子在第一象限运动的时间为t1=T=;同理,在第四象限运动的时间为t2=T'=;完成一次周期性运动的时间为t1+t2=,故B正确。由r=,知粒子做圆周运动的半径与B成反比,则粒子在x轴上方和下方两磁场中运动的半径之比为1∶2,故C正确。根据几何知识得:粒子第二次射入x轴上方磁场时,沿x轴前进的距离为x=r+2r=3r,故D正确。‎ ‎8.‎ ‎(2017·山东德州期末)右图是一个回旋加速器示意图,其核心部分是两个D形金属盒,两金属盒置于匀强磁场中,并分别与高频电源相连。现分别加速氘核H)和氦核He),下列说法中正确的是(　　)‎ A.它们的最大速度相同 B.它们的最大动能相同 C.两次所接高频电源的频率相同 D.仅增大高频电源的频率可增大粒子的最大动能 答案AC 解析由r=得最大速度v=,两粒子的相同,所以最大速度相同,A正确;最大动能Ek=mv2,因为两粒子的质量不同,最大速度相同,所以最大动能不同,B错误;高频电源的频率f=,因为相同,所以两次所接高频电源的频率相同,C正确;粒子的最大动能与高频电源的频率无关,D错误。‎ 二、实验题(10分)‎ ‎9.利用霍尔效应可以测量磁感应强度。如图甲所示,将导体置于磁场中,沿垂直磁场方向通入电流,在导体中垂直于电流和磁场的方向上会产生一个纵向电势差UH,这种现象叫霍尔效应。导体材料中单位体积内的自由电荷数目为n,自由电荷所带电荷量为q,将k=定义为霍尔系数。利用霍尔系数k已知的材料制成探头,其工作面(相当于图甲中垂直磁场的abb'a'面)的面积可以做到很小,因此可用来较精确测量空间某一位置的磁感应强度。‎ 图乙为一种利用霍尔效应测磁感应强度的仪器,其中的探头固定在探杆的前端,且使探头的工作面与探杆垂直。这种仪器既可以控制通过探头的电流I 的大小,又可以测出探头所产生的霍尔电势差UH,并自动计算出探头所测位置磁场的磁感应强度大小。‎ ‎(1)在利用上述仪器测量磁感应强度的过程中,对探杆的放置方位的要求是 ‎ ‎　。 ‎ ‎(2)计算所测位置磁感应强度,除了k、I、UH外,还需要知道哪个物理量　　　　(请填写下面选项前的字母)。 ‎ A.探头沿磁场方向的厚度l B.探头产生电势差两面间的距离h C.探头沿电流方向的长度l0‎ 用上述物理量表示所测磁感应强度大小B=　。 ‎ 答案(1)使探杆与磁场方向平行(或调整探杆的放置方位使霍尔电势差达到最大)　(2)A　‎ 解析(1)由题给信息易知,应使探杆与磁场方向平行(或调整探杆的放置方位使霍尔电势差达到最大);(2)自由电荷在运动过程中受到的电场力和洛伦兹力是一对平衡力,即qvB=q,I=nqvhl,k=,联立可得B=。所以还需要知道l。‎ 三、计算题(本题共3小题,共42分)‎ ‎10.‎ ‎(12分)(2017·辽宁五校协作体联考)如图所示,在xOy平面第一象限内有平行于y轴的匀强电场和垂直于xOy平面的匀强磁场,匀强电场的电场强度为E。一电荷量为+q的小球从y轴上离坐标原点距离为l的A点处,以沿x轴正方向的初速度进入第一象限,如果电场和磁场同时存在,小球将做匀速圆周运动,并从x轴上距坐标原点的C点离开磁场。如果只撤去磁场,并且将电场反向,带电小球以相同的初速度从A点进入第一象限,仍然从x轴上距坐标原点的C点离开电场。求:‎ ‎(1)小球从A点出发时的初速度大小;‎ ‎(2)磁感应强度B的大小。‎ 答案(1)　(2)‎ 解析(1)由带电小球做匀速圆周运动知 mg=qE ①‎ 所以电场反向后,由牛顿第二定律有 mg+qE=ma ②‎ 小球做类平抛运动有 l=at2 ③‎ ‎=v0t ④‎ 由①②③④联立得 v0=。 ⑤‎ ‎(2)带电小球做匀速圆周运动时,洛伦兹力提供向心力,则 qv0B= ⑥‎ 由几何知识得 ‎(l-r)2+l2=r2 ⑦‎ 由⑤⑥⑦得B=。‎ ‎11.(14分)‎ 如图,A、C两点分别位于x轴和y轴上,∠OCA=30°,OA的长度为l。在△OCA区域内有垂直于xOy平面向里的匀强磁场。质量为m、电荷量为q 的带正电粒子,以平行于y轴的方向从OA边射入磁场。已知粒子从某点射入时,恰好垂直于OC边射出磁场,且粒子在磁场中运动的时间为t0。不计重力。‎ ‎(1)求磁场的磁感应强度的大小;‎ ‎(2)若粒子先后从两不同点以相同的速度射入磁场,恰好从OC边上的同一点射出磁场,求该粒子这两次在磁场中运动的时间之和;‎ ‎(3)若粒子从某点射入磁场后,其运动轨迹与AC边相切,且在磁场内运动的时间为t0,求粒子此次入射速度的大小。‎ 答案(1)　(2)2t0　(3)‎ 解析(1)粒子在磁场中做匀速圆周运动,在时间t0内其速度方向改变了90°,故其周期T=4t0 ①‎ 设磁感应强度大小为B,粒子速度为v,圆周运动的半径为r,由洛伦兹力公式和牛顿运动定律得qvB=m ②‎ 匀速圆周运动的速度满足v= ③‎ 联立①②③式得B=。 ④‎ 甲 ‎(2)设粒子从OA边两个不同位置射入磁场,能从OC边上的同一点P射出磁场,粒子在磁场中运动的轨迹如图甲所示。‎ 设两轨迹所对应的圆心角分别为θ1和θ2。‎ 由几何关系有θ1=180°-θ2 ⑤‎ 粒子两次在磁场中运动的时间分别为t1与t2,则 t1+t2==2t0。 ⑥‎ 乙 ‎(3)如图乙,由题给条件可知,该粒子在磁场区域中的轨迹圆弧对应的圆心角为150°。设O'为圆弧的圆心,圆弧的半径为r0,圆弧与AC相切于B点,从D点射出磁场,由几何关系和题给条件可知,此时有∠OO'D=∠BO'A=30°⑦‎ r0cos∠OO'D+=l ⑧‎ 设粒子此次入射速度的大小为v0,由圆周运动规律 v0= ⑨‎ 联立①⑦⑧⑨式得v0= ⑩‎ ‎12.(16分)(2017·河南洛阳模拟)如图甲所示,y轴右侧空间有垂直xOy平面向里随时间变化的磁场,同时还有沿y轴负方向的匀强电场(图中电场未画出),磁感应强度随时间变化规律如图乙所示(图中B0已知,其余量均为未知)。t=0时刻,一质量为m、电荷量为+q的带电粒子以速度v0从坐标原点O沿x轴正方向射入电场和磁场区域,t0时刻粒子到达坐标为(x0,y0)的点A(x0>y0),速度大小为v,方向沿x轴正方向,此时撤去电场,t2时刻粒子经过x轴上x=x0点,速度沿x轴正方向,不计粒子重力,求:‎ ‎(1)0~t0时间内O、A两点间电势差UOA;‎ ‎(2)粒子在t=0时刻的加速度大小a;‎ ‎(3)B1的最小值和B2的最小值的表达式。‎ 答案(1)　(2)　(3)‎ 解析(1)带电粒子由O点到A点运动过程中,由动能定理得 qUOA=mv2-‎ 解得UOA=。‎ ‎(2)设电场强度大小为E,则 ‎-UOA=UAO=Ey0‎ t=0时刻,由牛顿第二定律得 qv0B0-qE=ma 解得a=。‎ ‎(3)如右图所示,t0~t1时间内,粒子在小的虚线圆上运动,相应小圆最大半径为r,对应的磁感应强度最小值为B1,则 r=‎ 又qvB1=m 解得B1的最小值B1=‎ t1时刻粒子从C点切入大圆,大圆最大半径为x0,对应的磁感应强度的最小值为B2,则 qvB2=m B2=。‎