2018-2019学年甘肃省静宁县第一中学高二10月月考数学（文）试题 Word版

2018-2019学年甘肃省静宁县第一中学高二10月月考数学（文）试题 Word版

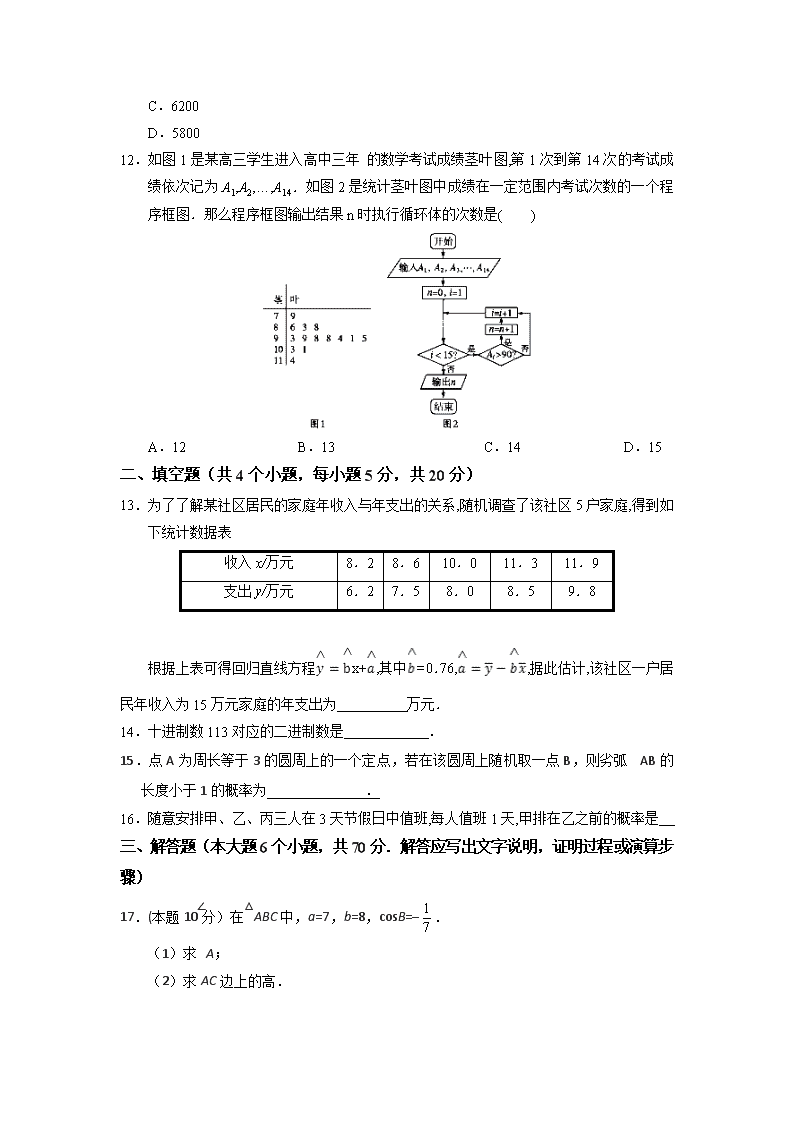
静宁一中2018-2019学年高二级第一学期月考试题（卷）‎ 文科数学 ‎(满分：150分 时间：120分钟)‎ 一、选择题（共12个小题，每小题5分，共60分）‎ ‎1．下列说法正确的是(　　)‎ A．甲、乙二人比赛，甲胜的概率为，则比赛5场，甲胜3场 B．某医院治疗一种疾病的治愈率为10%，前9个病人没有治愈，则第10个病人一定治愈 C．随机试验的频率与概率相等 D．天气预报中，预报明天降水概率为90%，是指降水的可能性是90%‎ ‎2．从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B={抽到二等品},事件C={抽到三等品},且已知P(A)=0．65,P(B)=0．2,P(C)=0．1．则事件“抽到的是二等品或三等品”的概率为(　　)‎ A．0．7 B．0．‎65 C．0．35 D．0．3‎ ‎3．已知某商场新进3000袋奶粉，为检查其三聚氰胺是否超标，先采用系统抽样的方法从中抽取200袋检查，若第五十一组抽出的号码是757，则第一组抽出的号码是（ ）‎ A．5 B．‎6 C． 7 D．8‎ ‎4．当m=7,n=3时,执行如图所示的程序框图,输出的S值为(　　)‎ A．7 ‎ B．42 ‎ C．210 ‎ D．840‎ ‎5．下列说法：‎ ‎ ①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；‎ ‎ ②设有一个回归方程，变量增加一个单位时，平均增加5个单位；‎ ‎ ③线性回归方程必过点；‎ ‎ ④曲线上的点与该点的坐标之间具有相关关系．‎ ‎ 其中错误的个数是（ ）‎ A．1 B．‎2 C．3 D．4‎ ‎6．甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示, 分别表示甲、乙两名运动员这项测试成绩的平均数,分别表示甲、乙两名运动员这项测试成绩的方差,则有(　　)‎ A． ‎ B． C． ‎ D． ‎7． 向边长为2的正方形中随机撒一粒豆子，则豆子落在正方形的内切圆的概率是（ ）‎ A． B． C． D． ‎ ‎8．从装有2个红球和2个黑球的口袋内任取2个球，那么互斥而不对立的两个事件是（ ）‎ A．至少有一个黑球与都是黑球 B．至少有一个黑球与都是红球 C．恰有1个黑球与恰有2个黑球 D．至少有一个黑球与至少有1个红球 ‎9．用秦九韶算法计算多项式在的值时，其中（最内层的括号到最外层括号的值依次赋予变量）的值为( )‎ A．27 B．‎60 C．63 D．118‎ ‎10．执行如图所示的程序框图,若输出的值为8,则判断框内可填入的条件是(　　)‎ A．‎ ‎ ‎ ‎ ‎ B．‎ C. ‎ ‎ C．‎ D．‎ ‎11．某电子商务公司对10 000名网络购物者2017年度的消费情况进行统计, 发现消费金额(单位 ‎ 万元)都在区间[0．3,0．9]内,其频率分布直方图如图所示．在这些购物者中,消费金额在区间 ‎ ‎[0．5,0．9]内的购物者的人数为 ( ) ‎ A．6000 ‎ B．5000 ‎ C．6200 ‎ D．5800‎ ‎12．如图1是某高三学生进入高中三年 的数学考试成绩茎叶图,第1次到第14次的考试成绩依次记为A1,A2,…,A14．如图2是统计茎叶图中成绩在一定范围内考试次数的一个程序框图．那么程序框图输出结果n时执行循环体的次数是(　　)‎ A．12 B．‎13 ‎ C．14 D．15‎ 二、填空题（共4个小题，每小题5分，共20分）‎ ‎13．为了了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表 ‎ 收入x/万元 ‎8．2‎ ‎8．6‎ ‎10．0‎ ‎11．3‎ ‎11．9‎ 支出y/万元 ‎6．2‎ ‎7．5‎ ‎8．0‎ ‎8．5‎ ‎9．8‎ 根据上表可得回归直线方程x+,其中=0．76,,据此估计,该社区一户居民年收入为15万元家庭的年支出为　　　　　万元． ‎ ‎14．十进制数113对应的二进制数是 ．‎ ‎15．点A为周长等于3的圆周上的一个定点，若在该圆周上随机取一点B，则劣弧AB的长度小于1的概率为 ．‎ ‎16．随意安排甲、乙、丙三人在3天节假日中值班,每人值班1天,甲排在乙之前的概率是　　　　　‎ 三、解答题（本大题6个小题，共70分．解答应写出文字说明，证明过程或演算步骤）‎ ‎17．(本题10分）在△ABC中，a=7，b=8，cosB=–． （1）求∠A；‎ ‎（2）求AC边上的高．‎ ‎18．(本题12分）通过市场调查,得到某种产品的资金投入x(单位 万元)与获得的利润y(单位 万元)的数据,如表所示 ‎ 资金投入x ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 利润y ‎2‎ ‎3‎ ‎5‎ ‎6‎ ‎9‎ ‎（1）)画出数据对应的散点图;‎ ‎（2）根据上表提供的数据,用最小二乘法求线性回归直线方程x+;‎ ‎（3）)现投入资金10万元,求获得利润的估计值为多少万元?‎ ‎ ‎ ‎19．(本题12分）我校对高二600名学生进行了一次知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图．‎ 分　组 频　数 频　率 ‎[50,60)‎ ‎2‎ ‎0．04‎ ‎[60,70)‎ ‎8‎ ‎0．16‎ ‎[70,80)‎ ‎10‎ ‎[80,90)‎ ‎[90,100]‎ ‎14‎ ‎0．28‎ 合　计 ‎1．00‎ ‎（1）填写频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;‎ ‎（2）请你估算该年级学生成绩的中位数;‎ ‎（3）如果用分层抽样的方法从样本分数在[60,70)和[80,90)的人中共抽取6人,再从6人中选2人,求2人分数都在[80,90)的概率．‎ ‎20．(本题12分）一个盒子里装有三张卡片，分别标记有数字1，2，3，这三张卡片除标记的数字外完全相同．随机有放回地抽取3次，每次抽取1张，将抽取的卡片上的数字依次记为a，b，c．‎ ‎（1）求“抽取的卡片上的数字满足a＋b＝c”的概率；‎ ‎（2）求“抽取的卡片上的数字a，b，c不完全相同”的概率．‎ ‎21．(本题12分）有关部门要了解甲型流感预防知识在学校的普及情况，命制了一份有10道题的问卷到各学校做问卷调查．某中学、两个班各被随机抽取5名学生接受问卷调查，班5名学生得分为：5、8、9、9、9，班5名学生得分为：6、7、8、9、10．‎ ‎（1）请你判断、两个班中哪个班的问卷得分要稳定一些，并说明你的理由；‎ ‎（2）如果把班5名学生的得分看成一个总体，并用简单随机抽样方法从中抽取样本容量为2的样本，求样本平均数与总体平均数之差的绝对值不小于1的概率．‎ ‎22．(本题12分）已知是公差为3的等差数列，数列满．‎ ‎（1）求的通项公式；‎ ‎（2）求的前n项和．‎ ‎2018-2019学年静宁一中高二数学月考试（题）卷答案 ‎ 文科数学 一． 选择题 ‎1.D 2.D 3.C 4.C 5.B 6.B 7.D 8.C 9.D 10.C 11.A 12.C 二． 填空题 13. ‎ 11.8 14. 1110001(2) 15. 16. ‎ 三．解答题 ‎17.解：（Ⅰ）在△ABC中，∵cosB=–，∴B∈（，π），∴sinB=．‎ 由正弦定理得=，∴sinA=．‎ ‎∵B∈（，π），∴A∈（0，），∴∠A=．‎ ‎（Ⅱ）在△ABC中，∵sinC=sin（A+B）=sinAcosB+sinBcosA==．‎ 如图所示，在△ABC中，∵sinC=，∴h==，‎ ‎∴AC边上的高为．‎ ‎18.(1)作出散点图如下 ‎ ‎(2)=4,‎ =5.‎ xiyi=2×2+3×3+4×5+5×6+6×9=117,=22+32+42+52+62=90,‎ ‎∴=1.7,=5-1.7×4=-1.8.‎ ‎∴线性回归方程为=1.7x-1.8.‎ ‎(3)当x=10时,=1.7×10-1.8=15.2(万元),‎ ‎∴当投入资金10万元,获得利润的估计值为15.2万元.‎ ‎19. (1)填写频率分布表中的空格,如下表 ‎ 分　组 频　数 频　率 ‎[50,60)‎ ‎2‎ ‎0.04‎ ‎[60,70)‎ ‎8‎ ‎0.16‎ ‎[70,80)‎ ‎10‎ ‎0.2‎ ‎[80,90)‎ ‎16‎ ‎0.32‎ ‎[90,100]‎ ‎14‎ ‎0.28‎ 合　计 ‎50‎ ‎1.00‎ 补全频率分布直方图,如下图 ‎ ‎(2)设中位数为x,依题意得0.04+0.16+0.2+0.032×(x-80)=0.5,‎ 解得x=83.125,所以中位数约为83.125.‎ ‎(3)由题意知样本分数在[60,70)有8人,样本分数在[80,90)有16人,‎ 用分层抽样的方法从样本分数在[60,70)和[80,90)的人中共抽取6人,‎ 则抽取的分数在[60,70)和[80,90)的人数分别为2人和4人.‎ 记分数在[60,70)的为a1,a2,在[80,90)的为b1,b2,b3,b4.‎ 从已抽取的6人中任选两人的所有可能结果有15种,分别为{a1,a2},{a1,b1},{a1,b2},{a1,b3},{a1,b4},{a2,b1},{a2,b2},{a2,b3},{a2,b4},{b1,b2},{b1,b3},{b1,b4},{b2,b3},{b2,b4},{b3,b4},‎ 设“2人分数都在[80,90)”为事件A,‎ 则事件A包括{b1,b2},{b1,b3},{b1,b4},{b2,b3},{b2,b4},{b3,b4}共6种,所以P(A)=.‎ ‎20.　(1)由题意知，(a，b，c)所有的可能为 ‎(1，1，1)，(1，1，2)，(1，1，3)，(1，2，1)，(1，2，2)，(1，2，3)，(1，3，1)，(1，3，2)，(1，3，3)，(2，1，1)，(2，1，2)，(2，1，3)，(2，2，1)，(2，2，2)，(2，2，3)，(2，3，1)，(2，3，2)，(2，3，3)，(3，1，1)，(3，1，2)，(3，1，3)，(3，2，1)，(3，2，2)，(3，2，3)，(3，3，1)，(3，3，2)，(3，3，3)，共27种．‎ 设“抽取的卡片上的数字满足a＋b＝c”为事件A，‎ 则事件A包括(1，1，2)，(1，2，3)，(2，1，3)，共3种．‎ 所以P(A)＝＝.‎ 因此，“抽取的卡片上的数字满足a＋b＝c”的概率为.‎ ‎(2)设“抽取的卡片上的数字a，b，c不完全相同”为事件B，则事件B包括(1，1，1)，(2，2，2)，(3，3，3)，共3种．‎ 所以P(B)＝1－P(B)＝1－＝.‎ 因此，“抽取的卡片上的数字a，b，c不完全相同”的概率为.‎ ‎21.解：（1） ‎ ‎ ， ‎ 因为 ‎ 所以B班的问卷得分更稳定一些。‎ (2) 取得的样本可能为（6,7）、（6,8）、（6,9）、（6,10）（7,8）、（7,9）（7,10）、（8,9）（8,10）、（9,10）共10种结果.‎ ‎ 对应的平均数为6.5、7、7.5、8、7.5、8、8.5、8.5、9、9.5，‎ 设事件C表示“样本平均数与总体平均数之差的绝对值不小于‎1”‎ 因为所以事件C包含的可能结果有4种，‎ 因此 ‎22. 解：（I）由已知，得得，所以数列是首项为2，公差为3的等差数列，通项公式为.‎ ‎（II）由（I）和 ，得，因此是首项为1，公比为的等比数列.记的前项和为，则