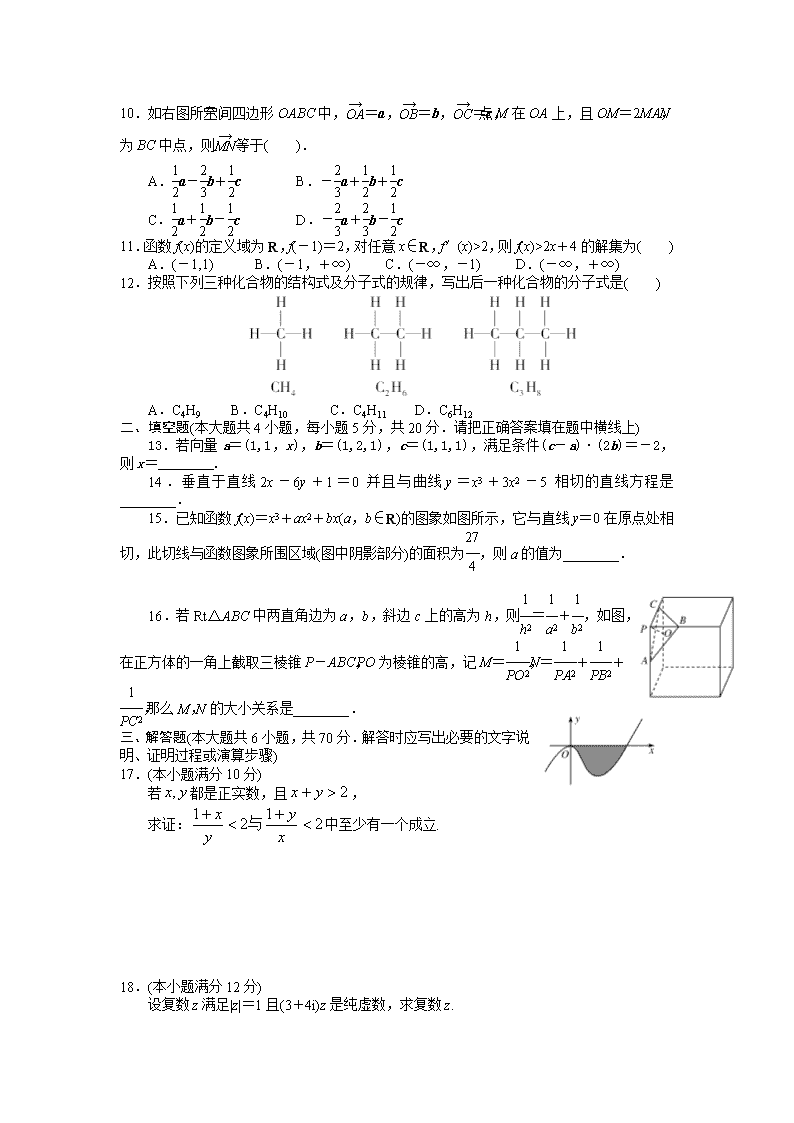数学理（普通班）卷·2018届山东省微山县第一中学高二下学期期中迎考（第二次月考）（2017-04）

数学理（普通班）卷·2018届山东省微山县第一中学高二下学期期中迎考（第二次月考）（2017-04）

高二年级迎期中考试训练（跃理、卓理）‎ 数 学 试 题 一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1．复数z＝(i为虚数单位)在复平面内对应的点所在象限为(　　)‎ A．第一象限　 　B．第二象限 C．第三象限 D．第四象限 ‎2．函数f(x)＝x3＋4x＋5的图象在x＝1处的切线在x轴上的截距为(　　)‎ A．10 B．5 C．－1 D．－ ‎3．下面几种推理中是演绎推理的为(　　)‎ A．由金、银、铜、铁可导电，猜想：金属都可导电 B．猜想数列，，，…的通项公式为an＝(n∈N＋)‎ C．半径为r的圆的面积S＝πr2，则单位圆的面积S＝π D．由平面直角坐标系中圆的方程为(x－a)2＋(y－b)2＝r2，推测空间直角坐标系中球的方程为 ‎(x－a)2＋(y－b)2＋(z－c)2＝r2‎ ‎4．函数y＝x3－3x2－9x(－21(n∈N＋)时，在验证n＝1时，左边的代数式为(　　)‎ A．＋＋ B．＋ C． D．1‎ ‎8．函数y＝ax3－x在(－∞，＋∞)上的减区间是[－1,1]，则(　　)‎ A．a＝ B．a＝1 C．a＝2 D．a≤0‎ ‎9．若z1，z2∈C，则z12＋1z2是(　　)‎ A．纯虚数 B．实数 C．虚数 D．不能确定 ‎10．如右图所示，空间四边形OABC中，＝a，＝b，＝c，点M在OA上，且OM＝2MA，N为BC中点，则等于(　　)．‎ A．a－b＋c B．－a＋b＋c C．a＋b－c D．－a＋b－c ‎11．函数f(x)的定义域为R，f(－1)＝2，对任意x∈R，f′(x)>2，则f(x)>2x＋4的解集为(　　)‎ A．(－1,1) B．(－1，＋∞) C．(－∞，－1) D．(－∞，＋∞)‎ ‎12．按照下列三种化合物的结构式及分子式的规律，写出后一种化合物的分子式是(　　)‎ A．C4H9 B．C4H10 C．C4H11 D．C6H12‎ 二、填空题(本大题共4小题，每小题5分，共20分．请把正确答案填在题中横线上)‎ ‎13．若向量a＝(1,1，x)，b＝(1,2,1)，c＝(1,1,1)，满足条件(c－a)·(2b)＝－2，则x＝________.‎ ‎14．垂直于直线2x－6y＋1＝0并且与曲线y＝x3＋3x2－5相切的直线方程是________．‎ ‎15．已知函数f(x)＝x3＋ax2＋bx(a，b∈R)的图象如图所示，它与直线y＝0在原点处相切，此切线与函数图象所围区域(图中阴影部分)的面积为，则a的值为________．‎ ‎16．若Rt△ABC中两直角边为a，b，斜边c上的高为h，则＝＋，如图，在正方体的一角上截取三棱锥P－ABC，PO为棱锥的高，记M＝，N＝＋＋，那么M，N的大小关系是________．‎ 三、解答题(本大题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤)‎ ‎17．(本小题满分10分)‎ 若都是正实数，且，‎ 求证：中至少有一个成立.‎ ‎18．(本小题满分12分)‎ 设复数z满足|z|＝1且(3＋4i)z是纯虚数，求复数z.‎ ‎19．(本小题满分12分)‎ 已知函数f(x)＝ax3＋bx＋1的图象经过点(1，－3)且在x＝1处，f(x)取得极值．求：‎ ‎(1)函数f(x)的解析式；‎ ‎(2)f(x)的单调递增区间．‎ ‎20．(本小题满分12分) ‎ 如图所示，在三棱锥S—ABC中，SO⊥平面ABC，侧面 SAB与SAC均为等边三角形，∠BAC＝90°，O为BC的中点，求二面角A—SC—B的余弦值．‎ ‎21．(本小题满分12分)‎ 用数学归纳法证明：‎ ＋＋…＋＝(n∈N*)．‎ ‎22．(本小题满分12分) ‎ 已知f(x)＝－x3＋ax，其中a∈R，g(x)＝，且f(x)＜g(x)在(0,1]上恒成立．求实数a的取值范围．‎ 高二年级迎期中考试训练跃理、卓理）‎ 数学参考答案 一、 选择题 DDCCC、DAABB、BB 二、 填空题 ‎13、2 14、 15、－3 16、M＝N 三、 解答题 ‎17、证明：假设.‎ 即：‎ 与矛盾.‎ 即中至少有一个成立.‎ ‎18、解：设z＝a＋bi(a，b∈R)，由|z|＝1，得＝1. ①‎ ‎(3＋4i)z＝(3＋4i)(a＋bi)＝3a－4b＋(4a＋3b)i是纯虚数，则3a－4b＝0. ②‎ 联立①②解得或 所以z＝＋i或z＝－－i.‎ ‎19、解：(1)由f(x)＝ax3＋bx＋1的图象过点(1，－3)得a＋b＋1＝－3，‎ ‎∵f′(x)＝3ax2＋b，‎ 又f′(1)＝3a＋b＝0，‎ ‎∴由得，‎ ‎∴f(x)＝2x3－6x＋1.‎ ‎(2)∵f′(x)＝6x2－6，‎ ‎∴由f′(x)>0得x>1或x<－1，‎ ‎∴f(x)的单调递增区间为(－∞，－1)，(1，＋∞)．‎ ‎20、解：‎ 以O为坐标原点，射线OB，OA，OS分别为x轴、y轴、z轴的正半轴，建立如图所示的空间直角坐标系Oxyz.设B(1,0,0)，则C(－1,0,0)，A(0,1,0)，S(0,0,1)，SC的中点M.‎ 故＝，＝，‎ ＝(－1,0，－1)，‎ 所以·＝0，·＝0.‎ 即MO⊥SC， MA⊥SC.‎ 故〈，〉为二面角A—SC—B的平面角．‎ cos〈，〉＝＝.‎ 即二面角A—SC—B的余弦值为.‎ ‎21、解：①当n＝1时，左边＝＝，‎ 右边＝＝，‎ 左边＝右边，等式成立．‎ ‎②假设n＝k(k≥1)时，等式成立．‎ 即＋＋…＋＝，‎ 当n＝k＋1时，左边 ‎＝＋＋…＋＋ ‎＝＋＝ ‎＝＝，‎ 所以当n＝k＋1时，命题成立．‎ 由①②可得对任意n∈N*，等式成立．‎ ‎22、解：令F(x)＝f(x)－g(x)‎ ‎＝－x3＋ax＋x，‎ 即F(x)＜0在(0,1]上恒成立，‎ 所以a＜x2－x在(0,1]上恒成立，‎ 令h(x)＝x2－x，‎ h′(x)＝2x－＝ ‎＝，‎ 令h′(x)＞0，又x∈(0,1]，‎ 得x∈，令h′(x)＜0，‎ 又x∈(0,1]得x∈.‎ 所以h(x)最小值＝h＝－.‎ 即a＜－.‎