2016年北京市海淀区高考数学一模试卷（文科）

申明敬告： 本站不保证该用户上传的文档完整性，不预览、不比对内容而直接下载产生的反悔问题本站不予受理。

文档介绍

2016年北京市海淀区高考数学一模试卷（文科）

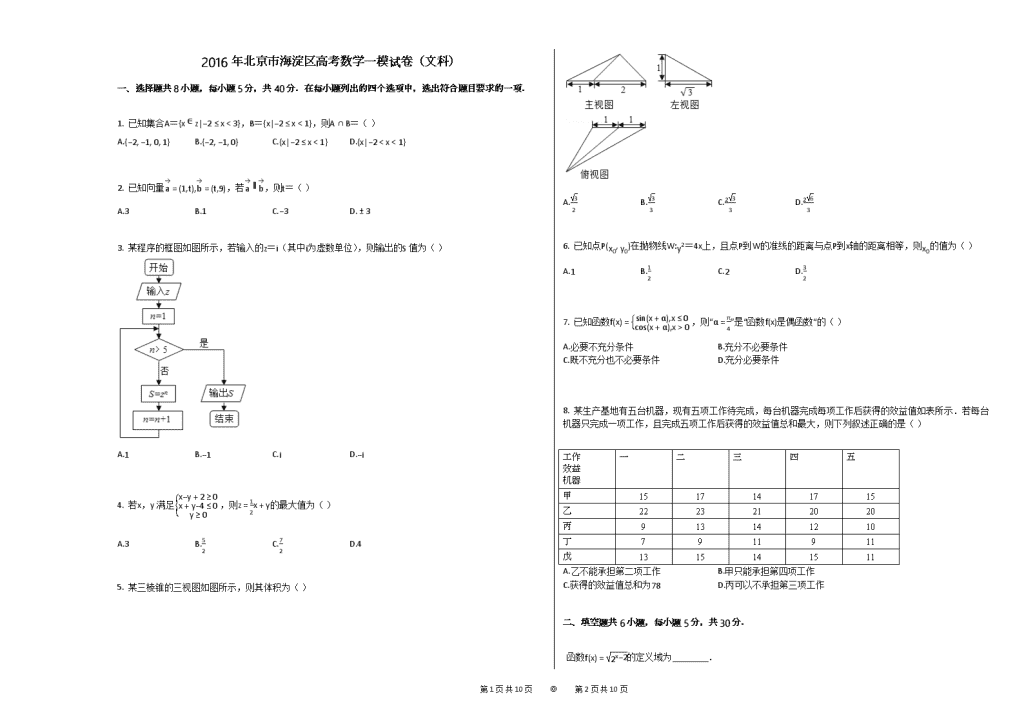
‎2016年北京市海淀区高考数学一模试卷（文科）‎ 一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．‎ ‎ ‎ ‎1. 已知集合A＝‎{x∈z|−2≤x<3}‎，B＝‎{x|−2≤x<1}‎，则A∩B＝（ ） ‎ A.‎{−2, −1, 0, 1}‎ B.‎{−2, −1, 0}‎ C.‎{x|−2≤x<1}‎ D.‎‎{x|−20‎ ‎，则“α=‎π‎4‎”是“函数f(x)‎是偶函数“的（ ） ‎ A.必要不充分条件 B.充分不必要条件 C.既不充分也不必要条件 D.充分必要条件 ‎ ‎ ‎ ‎8. 某生产基地有五台机器，现有五项工作待完成，每台机器完成每项工作后获得的效益值如表所示．若每台机器只完成一项工作，且完成五项工作后获得的效益值总和最大，则下列叙述正确的是（ ） ‎ 工作 效益 机器 一 二 三 四 五 甲 ‎15‎ ‎17‎ ‎14‎ ‎17‎ ‎15‎ 乙 ‎22‎ ‎23‎ ‎21‎ ‎20‎ ‎20‎ 丙 ‎9‎ ‎13‎ ‎14‎ ‎12‎ ‎10‎ 丁 ‎7‎ ‎9‎ ‎11‎ ‎9‎ ‎11‎ 戊 ‎13‎ ‎15‎ ‎14‎ ‎15‎ ‎11‎ A.乙不能承担第二项工作 B.甲只能承担第四项工作 C.获得的效益值总和为‎78‎ D.丙可以不承担第三项工作 ‎ 二、填空题共6小题，每小题5分，共30分．‎ ‎ ‎ ‎ 函数f(x)=‎‎2‎x‎−2‎的定义域为________． ‎ 第9页 共10页 ◎ 第10页 共10页 ‎ ‎ ‎ 已知数列‎{an}‎的前n项和为Sn，且Sn‎=n‎2‎−4n，则a‎2‎‎−‎a‎1‎＝________． ‎ ‎ ‎ ‎ 已知l为双曲线C:x‎2‎a‎2‎−y‎2‎b‎2‎=1‎的一条渐近线，其倾斜角为π‎4‎，且C的右焦点为‎(2, 0)‎，则C的右顶点为________，C的方程为________． ‎ ‎ ‎ ‎ 在‎1‎‎2‎‎,‎2‎‎1‎‎3‎.log‎3‎2‎这三个数中，最小的数是________． ‎ ‎ ‎ ‎ 已知函数f(x)‎＝sin(2x+φ)‎，若f(π‎12‎)−f(−‎5π‎12‎)=2‎，则函数f(x)‎的单调增区间为________． ‎ ‎ ‎ ‎ 给定正整数k≥2‎，若从正方体ABCD−‎A‎1‎B‎1‎C‎1‎D‎1‎的‎8‎个顶点中任取k个顶点，组成一个集合M＝‎{X‎1‎, X‎2‎, ..., Xk}‎，均满足‎∀‎Xi，Xj‎∈M，‎∃‎X‎1‎，Xt‎∈M，使得直线XiXj‎⊥‎X‎1‎Xt，则k的所有可能取值是________． ‎ 三、解答题共6小题，共80分．解答应写出文字说明、演算步骤或证明过程．‎ ‎ ‎ ‎ 在‎△ABC 中，‎∠C=‎‎2π‎3‎，a＝‎6‎． ‎(‎Ⅰ‎)‎若c＝‎14‎，求sinA的值； ‎(‎Ⅱ‎)‎若‎△ABC的面积为‎3‎‎3‎，求c的值． ‎ ‎ ‎ ‎ 已知数列‎{an}‎是等比数列，其前n项和为Sn，满足S‎2‎‎+‎a‎1‎＝‎0‎，a‎3‎＝‎12‎． ‎(‎Ⅰ‎)‎求数列‎{an}‎的通项公式； ‎(‎Ⅱ‎)‎是否存在正整数n，使得Sn‎>2016‎？若存在，求出符合条件的n的最小值；若不存在，说明理由． ‎ ‎ ‎ ‎ 如图，在四棱锥P−ABCD中，PA⊥‎平面ABCD，四边形ABCD为正方形，点M，N分别为线段PB，PC上的点，MN⊥PB． ‎(‎Ⅰ‎)‎求证：平面PBC⊥‎平面PAB； ‎(‎Ⅱ‎)‎求证：当点M不与点P，B重合时，MN // ‎平面ABCD； ‎(‎Ⅲ‎)‎当AB＝‎3‎，PA＝‎4‎时，求点A到直线MN距离的最小值． ‎ ‎ ‎ ‎ 一所学校计划举办“国学”系列讲座．由于条件限制，按男、女生比例采取分层抽样的方法，从某班选出‎10‎人参加活动，在活动前，对所选的‎10‎名同学进行了国学素养测试，这‎10‎名同学的性别和测试成绩（百分制）的茎叶图如图所示． ‎(‎Ⅰ‎)‎根据这‎10‎名同学的测试成绩，分别估计该班男、女生国学素养测试的平均成绩； ‎(‎Ⅱ‎)‎这‎10‎名同学中男生和女生的国学素养测试成绩的方差分别为s‎1‎‎2‎，s‎2‎‎2‎，试比较s‎1‎‎2‎与s‎2‎‎2‎的大小（只需直接写出结果）； ‎(‎Ⅲ‎)‎若从这‎10‎名同学中随机选取一男一女两名同学，求这两名同学的国学素养测试成绩均为优良的概率．（注：成绩大于等于‎75‎分为优良） ‎ ‎ ‎ ‎ 已知椭圆C:x‎2‎a‎2‎+y‎2‎b‎2‎=1(a>b>0)‎的离心率为‎3‎‎2‎，椭圆C与y轴交于A、B两点，‎|AB|‎＝‎2‎． ‎(‎Ⅰ‎)‎求椭圆C的方程； ‎(‎Ⅱ‎)‎已知点P是椭圆C上的动点，且直线PA，PB与直线x＝‎4‎分别交于M、N两点，是否存在点P，使得以MN为直径的圆经过点‎(2, 0)‎？若存在，求出点P的横坐标；若不存在，说明理由． ‎ ‎ ‎ ‎ 已知函数f(x)=‎‎1−xex． ‎ ‎(1)‎求曲线y‎=f(x)‎在点（‎0, f(0)‎）处的切线方程；‎ ‎ ‎ ‎(2)‎求函数f(x)‎的零点和极值；‎ ‎ ‎ ‎(3)‎若对任意x‎1‎，x‎2‎‎∈[a, +∞)‎，都有f(x‎1‎)−f(x‎2‎)≥−‎‎1‎e‎2‎成立，求实数a的最小值．‎ 第9页 共10页 ◎ 第10页 共10页 参考答案与试题解析 ‎2016年北京市海淀区高考数学一模试卷（文科）‎ 一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．‎ ‎1.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 交集根助运算 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎2.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 平面水因共线（平行）的坐似表阻 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎3.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 程正然图 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎4.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 简单因性规斯 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎5.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 由三都问求体积 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎6.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 抛物使之性质 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎7.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 充分常件、头花条件滤充要条件 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎8.‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 进行简根的合情亮理 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 二、填空题共6小题，每小题5分，共30分．‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 函数的定较域熔其求法 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 第9页 共10页 ◎ 第10页 共10页 ‎【考点】‎ 数于术推式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 双曲根气离心率 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 对数值于小的侧较 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 正弦射可的图象 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 棱柱三实构特征 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 三、解答题共6小题，共80分．解答应写出文字说明、演算步骤或证明过程．‎ ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 正因归理 余于视理 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 等比数表的弹项公式 数使的种和 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 直线体平硫平行 平面因平面京直 点于虫、练板的距离计算 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 极差、使差与标香差 列举法体算土本母件数及骨件发生的概率 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 椭圆水明心率 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 ‎【答案】‎ 此题暂无答案 ‎【考点】‎ 利用导于研究轨函数成点有近的问题 利用都数资究不长式化成立问题 第9页 共10页 ◎ 第10页 共10页 利用三数定究曲纵上迹点切线方程 利来恰切研费函数的极值 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 此题暂无解答 第9页 共10页 ◎ 第10页 共10页
查看更多

相关文章

您可能关注的文档