- 2021-02-26 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江苏省G4联考:苏州中学、常州中学、盐城中学、扬州中学2020-2021学年上学期高三四校联考试卷数学试题
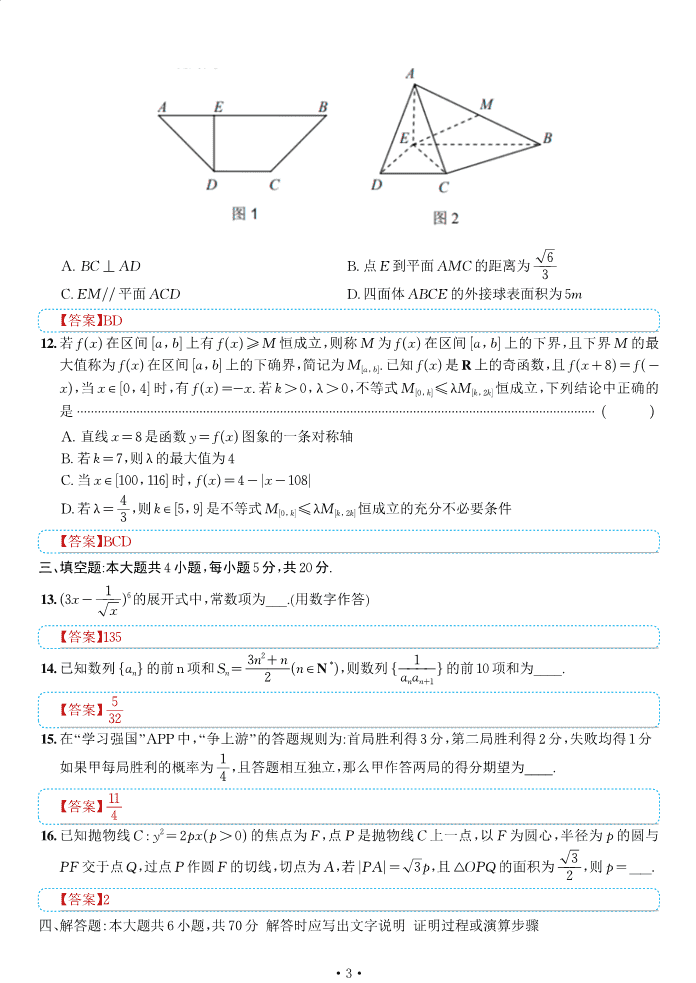
G4(苏州中学、常州中学、盐城中学、扬州中学)2021届高三联考 数学试题 2021.01 一、单项选择题:本大题共 8 题,每 题 5 ,共计 40 、 每 题给出的四个选项中,只有一项是符 题目要 的. 1.已知 A={x|x< 1},B={x|log2x≤ 0}, A∩B为 ( ) A. (0,1) B. (0,1] C. ( -∞,1) D. ( -∞,1)] 【答 】A 2.复数 z1= 2+ i,z2= 1- 3i,其中 i为虚数单 , z= z1 ⋅ z2 复 内的对 点 于 ( ) A. 第一 B.第二 C.第三 D.第四 【答 】D 3. 语文、数学、英语、物理 1 书,把这 4 书 放入 3个不 的抽 里,要 每个抽 至 放 一 书且语文 数学不 一个抽 里, 放法数为 ( ) A. 18 B. 24 C. 30 D. 36 【答 】C 4. 数学的 性学习中, 用函数的图 函数的性质,也 用函数的解 函数的性质, 下 函数的解 (其中 e= 2.71828...为自 对数的 数 )与所给图 契 的 ( ) A. y= 2sinx x2+ 1 B. y= 2x x2+ 1 C. y= ex- e-x ex+ e-x D. y= ex+ e-x ex- e-x 【答 】B 5.已知 ω> 0,φ ∈R,函数 f(x) = sin(ωx+ φ)图 相 的两个对称中 之间的距离为 d1,函数 g(x) = 2tan(ωx+ φ)图 相 的两个对称中 之间的距离为 d2, ( ) A. d1= 1 2 d2 B. d1= d2 C. d1= 2d2 D.d1= 4d2 【答 】C 6.已知双曲线C : y 2 a2 - x2 b2 = 1(a> 0,b> 0)的上、下顶点 为A1,A2,点P 双曲线C上 ( 于顶点 ),直线PA1,PA2的斜 乘积为 3 4 , 双曲线C的渐近线方 为 ( ) A. y=± 1 2 x B. y=± 3 2 x C. y=± 2 3 3 x D. y=± 2x ·1· 【答 】B 7.已知△ABC为等边三角 ,AB= 2,△ABC所 内的点P满足 |AP -AB -AC | = 1,|AP |的 值为 ( ) A. 3 - 1 B. 2 2 - 1 C. 2 3 - 1 D. 7 - 1 【答 】C 8.若 ex-a≥ lnx+ a对一 正实数 x恒成 , 实数 a的取值 围 ( ) A. ( -∞, 1 e ] B. ( -∞,1] C. ( -∞,2] D. ( -∞,e] 【答 】B 二、多项选择题:本大题共 4 题,每 题 5 ,共计 20 , 每 题给出的四个选项中,有多项符 题目 要 全部选对的得 5 ,部 选对的得 2 ,不选或有错选的得 0 . 9. 2020 1 18日,国家统计 公 了 2020 人 费支出的情况, 绘 了 图,已知 2020 2019 “其他用 及 ”中人 费支出大约 为 462元 524元, 结 2019 人 费支出情况,下 结论中正 的 ( ) A. 2020 “食 烟酒”项目的人 费支出所占总额的百 比 2019 的高 B. 2019 人 费支出约为 21833元 C. 2019 2020 “生 用 及 ”项目上的人 费支出相等 D. 2020 人 费支出比 2019 人 费支出 所 【答 】ABD 10.已知实数 a,b满足 a2- ab+ b= 0(a> 1),下 结论中正 的 ( ) A. b≥ 4 B. 2a+ b≥ 8 C. 1 a + 1 b > 1 D. ab≥ 27 4 【答 】AD 11.已知四边 ABCD 等 (如图 1),AB= 3,DC= 1,∠BAD= 45°,DE⊥AB. △ADE DE 折起, AE ⊥ EB( 如图 2),连结 AC,AB,设 M AB 的中点、下 结论中正 的 ( ) ·2· A. BC⊥AD B.点E AMC的距离为 6 3 C. EM// ACD D.四 ABCE的外 球表 积为 5m 【答 】BD 12.若 f(x) 区间 [a,b]上 f(x) ≥M恒成 , 称M为 f(x) 区间 [a,b]上的下界,且下界M的 大值称为 f(x) 区间 [a,b]上的下 界,简记为M[a,b].已知 f(x) R上的奇函数,且 f(x+ 8) = f( - x), x ∈ [0,4]时, f(x) =-x.若 k> 0,λ> 0,不等 M[0,k]≤ λM[k,2k]恒成 ,下 结论中正 的 ( ) A. 直线 x= 8 函数 y= f(x)图 的一 对称轴 B.若 k= 7, λ的 大值为 4 C. x ∈ [100,116]时,f(x) = 4- |x- 108| D.若 λ= 4 3 , k ∈ [5,9] 不等 M[0,k]≤ λM[k,2k]恒成 的充 不 要 件 【答 】BCD 三、填空题:本大题共 4 题,每 题 5 ,共 20 . 13. (3x- 1 x )6的 中, 数项为___.(用数字 答) 【答 】135 14.已知数 {an}的 n项 Sn= 3n2+ n 2 (n ∈N *), 数 { 1 anan+1 }的 10项 为____. 【答 】 5 32 15. “学习 国”APP中,“争上游”的答题规 为: 胜 3 ,第二 胜 2 ,失败 1 、 如 甲每 胜 的 为 1 4 ,且答题相互独 , 么甲 答两 的 为____. 【答 】 11 4 16.已知抛物线 C : y2= 2px(p> 0)的 点为F,点P 抛物线 C上一点,以F为 ,半 为 p的 与 PF交于点Q,过点P F的 线, 点为A,若 |PA| = 3 p,且△OPQ的 积为 3 2 , p=__. 【答 】2 四、解答题: 大题共6 题,共70 、解答时 写出文字说 、证 过 或 算步骤、 ·3· ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~ 17. ( 题满 10 ) ① 3 cosB= 2- 2sin B2 cos B2 ,② 3 bsinC= ccosB,③ (b+ a) (b- a) = c2- 3 ac三个 件中任 一 个,补充 下 的问题中, 进行解答、 问题 :已知△ABC的三边 a,b,c所对的角 为A,B,C,若 a= 4,c= 3 b,_____, △ABC 的 积 . 注 :如 择多个 件 解答, 第一个解答计 、 【规 解答】解: ①:由 3 cosB = 2- 2sinB2 cosB2 sinB + 3 cosB= 2,2 即 sin(B + π 3 )= 1,因为 B ∈(0,π),所以 B = π 6 . 4 ②:由正 定理 3 sin BsinC = sinCcosB,因为 sinC≠ 0 , 所以 3 sin B = cos B . 因为 cos B ≠ 0,所以 Btan = 3 3 .因为B ∈(0,π),所以B= π 6 . 4 ③:由题意 c2+ a2- b2= 3 ac, cosB = a2+ c2- b2 2ac = 3 ac 2ac = 3 2 . 2 因为 B ∈(0,π),所以B == π 6 . 4 又因为 Csin Bsin = c b = 3 ,所以 sinC= 3 sin B= 3 × 1 2 = 3 2 . 由C ∈(0,π),所以C = π 3 或C = 2π 3 . 6 C= π 3 时,A= π 2 ,又因为 a= 4,所以 b= 2,c= 2 3 . 积 S= 1 2 × 2× 2 3 = 2 3 . C= 2π 3 时,A= π 6 ,所以A=B.又因为 a= 4,所以 b= 4. 积 S= 1 2 × 4× 4× 3 2 = 4 3 . 综上所述,△ABC的 积为 2 3 或 4 3 . 10 18. ( 题满 12 ) 如图所示, 四棱锥 S-ABCD中, ABCD 正方 ,对角线AC与BD交于点F, SBC 边长为 2的等边三角 ,点E 棱BS上 . (1)若 SD// AEC, SE EB 的值; ·4· ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~ (2)若 SBC⊥ ABCD, 二 角B-AS-C的 值 . 【规 解答】(1)连结EF,∵ SD⎳ AEC,SD⊂ BSD, BSD∩ AEC=EF, ∴ SD⎳EF . 3 ∵ ABCD 正方 ,F为AC中点, ∴EF SD的中 线, SE EB = 1. 4 (2)取BC的中点为O,AD的中点为M,连结MO, MO ⏊ BC , 因为 SBC丄 ABCD, SBC∩ ABCD = BC ,OA⊂ ABCD, 所以OM丄 SBC. 5 又OS丄BC ,所以O为 原点 . 以{OS ,OC ,OM }为正交基 建 冋直角 系O- xyz, 6 A(0,-1,2),8(0,-1,0),C(0,1,0),S( 3 ,0,0),E 3 2 ,- 1 2 ,0 , 从 SC = (- 3 ,1,0),AC = (0,2,-2),AB = (0,0,-2),AS = ( 3 ,1, - 2), 设 ASC的法 量为m = (x,y,z), - 3 x+ y= 0, y- z= 0. 取 x= 1, y = 3 ,z = 3 , 所以 ASC的一个法 量为m= (1, 3 , 3 ). 8 设 ASB的法 量为 n = (x,y,z), -2z= 0, 3 x+ y- 2z= 0. 取 y= 3 , x=-1,z = 0, 所以 ASB的一个法 量为 n = (-1, 3 ,0) . 10 ∴ cos m,n = mn m n = 7 7 . ∵二 角B-AS-C的 角为锐角, ∴二 角B-AS-C的 值为 7 7 . 12 19. ( 题满 12 ) 已知数 {an}中,an> 1,a1= log23,且数 中任意相 两项具 2倍关系、记 an所 可能取值的 为An,其元 为 Sn(n ∈N *). (1)证 A2为单元 , 用 举法写出A5,A6; (2)由(1)的结 ,设 k ∈N*, 纳出A2k+1,A2k+2 (只要 写出结 ), S2k+1, 出 S2k+2与 S2k+1的倍数 关系. 【规 解答】 (1)证 :∵ a1 = 2log 3 ∈(1,2),1 数 中任意相 两项具 2倍关系,∴ a2= 1 2 a1或 2a1. ∴A2={2a1}为单元 . 3 由此, A3 ={a1 ,4a1},A4 ={2a1,8a1}, A5={a1,4a1,16a1},5 ·5· ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~ A6={2a1,8a1,32a1}. 6 (2)由(1)的结 , 纳 A2k+1={a1,4a1,16a1,⋯,4ka1},7 A2k+2 ={2a1,8a1,32a1,⋯,2× 4ka1}8 S2k+1= a1+ 4a1+ 16a1+⋯+4ka1= 4k+1- 1 3 a1= 4k+1- 1 3 2log 3,10 因为A2k+1中的每一个元 的两倍 成的 等于A2k+2, 所以 S2k+2= 2S2k+1. 12 20. ( 题满 12 ) 我国为全 建设社 主义 代化国家, 定了从 2021 2025 的 “十四五 ”规 、某 业为 国家号召, 聚科 量, 科技 新,准备 发资金、 该 业为了了解 发资金投入额 x(单 :亿元 )对 盈 额 y(单 :亿元 )的 , 了 “十二五 ” “十三五 ”规 发 间近 10 发资金投入额 xi 盈 额 yi的数 、 过对比 ,建 了两个函数模 :① y= α+ βx2,② y= eλx+t,其中 α,β,λ,t 为 数,e为自 对数的 数 .令 ui> x2 i ,vi= lnyi(i= 1,2,⋯,10), 经计算 如下数 : (1)请从相关系数的角 , 哪一个模 拟 更好? (2) (i) (1)的 择及表中数 ,建 y关于 x的回 方 ; (系数精 0.01) ( ii )若 2021 盈 额 y为 250亿元,请预 2021 的 发资金投入额 x为多 亿元? (结 精 0.01) :①相关系数 r= n i=1 (xi- x ) (yi- y ) n i=1 (xi- x )2 ∑ n i=1 (yi- y )2 , 回 直线 y = a + b x中 : b = n i=1 (xi- x ) (yi- y ) n i=1 (xi- x )2 ,a = y - b x ②参考数 : ln2≈ 0.693,ln5≈ 1.609 【规 解答】 解 ∶(1)设 ui yi 的相关系数为 r1,xi vi 的相关系数为 r2,由题意, ·6· ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~ r1= 10 i=1 ui- u yi- y 10 i=1 ui- u 2 10 i=1 yi- y 2 = 130 11250× 2 = 13 15 ≈ 0.87, 2 r2= 10 i=1 xi- x vi- v 10 i=1 xi- x 2 10 i=1 vi- v 2 = 12 65× 2.6 = 12 13 ≈ 0.92, 4 r1 < r2 ,因此从相关系数的角 ,模 y= eλx+t的拟 更好. (2)(i)先建 v关于 x的线性回 方 , 由 y= eλx+t, lny= t+ λx,即 v= t+ λx, λ = 10 i=1 xi- x vi- v 10 i=1 xi- x 2 = 12 65 ,7 t = v - λ x = 5.36- 12 65 × 26= 0.56, 8 所以 v关于 x的线性回 方 为 v = 0.18x+ 0.56, 所以 lny= 0.18x+ 0.56, y = e0.18x+0.56. 10 (ii)2021 盈 额 y= 250(亿元), 所以 250= e0.18x+0.56, 0.18x+ 0.56= ln250, 因为 ln 250= 3 ln 5+ ln 2≈ 3× 1.609+ 0.693= 5.52, 所 以 x≈ 5.52- 0.56 0.18 ≈ 27.56 . 所以 2021 的 发资金投入量约为 27.56亿元 . 12 21. ( 题满 12 ) 已知 C : x 2 a2 + y2 b2 = 1(a> b> 0)经过点P(2,1),且离 为 3 2 ,直线 l与 交于A,B两点, 线段AB的中点为M. (1) C的方 ; (2)若∠APB的角 线与 x轴 直, PM长 的 值 . 【规 解答】解 ∶(1)因为 经过点P且离 为 3 2 , 所以 22 a2 + 1 b2 = 1, c a = 3 2 , 其中 a² = b² + c², 2 解 a2= 8, b2= 2, 所以 方 为 x2 8 + y2 2 = 1. 4 (2)因为∠APB的角 线与 x轴 直,所以 kPA+ kPB= 0. 设直线PA的斜 为 k(k≠ 0), 直线PA的方 为 ∶ y= k(x- 2)+1, ·7· ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~ 由 y= k(x- 2) + 1, x2 8 + y2 2 = 1, (1+ 4k2)x2+ 8k(1- 2k)x+ 16k2- 16k- 4= 0. 所以 x1= 8k2- 8k- 2 1+ 4k2 ,代入 y1= -4k2- 4k+ 1 1+ 4k2 . 即A 8k2- 8k- 2 1+ 4k2 , -4k 2- 4k+ 1 1+ 4k2 , 理可 B 8k2+ 8k- 2 1+ 4k2 , -4k 2+ 4k+ 1 1+ 4k2 . 所以M 8k2- 2 1+ 4k2 , -4k 2+ 1 1+ 4k2 . 8 M 直线 x+ 2y= 0上,所以PM的 值为P 直线 x+ 2y= 0的距离 . 10 即 d= 2+ 2 5 = 4 5 5 ,此时M 6 5 ,- 3 5 内, 所以PM的 值为 4 5 5 . 12 (此处亦可用函数法处理:PM² = f(k)= 64k2+ 16 1+ 4k2 2 (k≠ 0)) 因此PM的 值为 4 5 5 . 22. ( 题满 12 ) 已知函数 f(x) = sinx 2+ cosx ,g(x) = a(ex- 1) (a为 数 ) (1) 函数 f(x) x= π 2 处的 线方 ; (2)设F x = f x + -1 ng x (n ∈Z). (i)若 n为偶数, a< 0时,函数F(x) 区间 (0,π 2 )上 值点, 实数 a的取值 围; ( ii )若 n为奇数,不等 F(x)≤ 0 [0,+∞)上恒成 , 实数 a的 值 . 【规 解答】解:(1)f(x)= cosx(2+ cosx)-sinx(-sinx) (2+ cosx)2 = 2cosx+ 1 (2+ cosx)2 . 2 f π 2 = 1 4 , x= π 2 时,f π 2 = 1 2 . ∴ f x x= π 2 处的 线方 为 y- 1 2 = 1 4 x- π 2 , 即 y= 1 4 x+ 4- π 8 . 3 (2) (i)n为偶数时,F(x)= f(x)+g(x)= xsin 2+ xcos + a(ex- 1), F(x) = 2cosx+ 1 2+ cosx 2 + a·ex,令 h(x)=F(x), h(x)= 2 xsin cosx- 1 2+ cosx 3 + a·ex. ∵ x∈ 0, π2 且 a< 0,∴ h(x)< 0 0, π2 恒成 . 4 ∴ h(x) 0, π2 单 减,其中 h(0)= 1 3 + a ,h π 2 = 1 4 + a ∙ e π 2 . ·8· ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~~ ∵F(x) 0, π2 值点, ∴ h(0)> 0且 h π 2 < 0,即 - 13 < a<- 1 4 e π 2 . - 1 3 < a<- 1 4 e π 2 时,∃ x0∈ 0, π2 , h(x0)= 0. 令F(x)> 0,即 h(x)> 0,F(x)(0,x0)单 ; 令F(x)< 0,即 h(x)< 0,F(x) x0, π 2 单 减 . ∴F(x) 0, π2 值点 . 因此实数 a的取值 围 - 1 3 ,- 1 4 e π 2 6 (ii)n为奇数时,F(x)= f(x)-g(x)≤ 0 0 ,+∞ 恒成 . x= 0时,F(0)= 0. x> 0时,因为F(x)= xsin 2 + xcos - a ex- 1 ≤ 0恒成 , 而F(x)= 2 x+ 1cos 2 + xcos 2 - a·ex, 令 t= 2+ cosx,t ∈ [1,3].m(t)= 2(t- 2) + 1 t2 = 2 t - 3 t3 ∈ -1, 13 . ∴ ex> e0= 1, ① a≥ 1 3 时,a·ex> 1 3 ,∴F(x)查看更多