2018-2019学年福建省龙海市程溪中学高二下学期期中考试 数学 Word版

2018-2019学年福建省龙海市程溪中学高二下学期期中考试 数学 Word版

福建省龙海市程溪中学2018--2019高二年下学期数学期中考试卷 一、选择题（本大题共12小题，共60.0分）‎ 1. ‎1+i‎-2i‎=(  )‎ A. ‎-‎1‎‎2‎-‎1‎‎2‎i B. ‎-‎1‎‎2‎+‎1‎‎2‎i C. ‎1‎‎2‎‎-‎1‎‎2‎i D. ‎‎1‎‎2‎‎+‎1‎‎2‎i 2. 函数f(x)=x‎3‎+x在点x=1‎处的切线方程为‎(  )‎ A. ‎4x-y+2=0‎ B. ‎4x-y-2=0‎ C. ‎4x+y+2=0‎ D. ‎‎4x+y-2=0‎ 3. 复数i‎3‎‎2i-1‎‎(i为虚数单位‎)‎的共轭复数是‎(  )‎ A. ‎-‎2‎‎5‎+‎1‎‎5‎i B. ‎2‎‎3‎‎+‎1‎‎3‎i C. ‎2‎‎3‎‎-‎1‎‎3‎i D. ‎‎-‎2‎‎5‎-‎1‎‎5‎i 4. 若‎1‎a‎(‎‎2x+‎1‎x)dx=3+ln2‎，则a的值是‎(  )‎ A. 6 B. 4 C. 3 D. 2‎ 5. 已知a∈R，i为虚数单位，若‎(1-i)(a+i)‎为纯虚数，则a的值为‎(  )‎ A. 2 B. 1 C. ‎-2‎ D. ‎‎-1‎ 6. 函数f(x)=‎exx的图象大致为‎(  )‎ A. B. C. D. ‎ 1. 已知f(x)=x‎2‎+3xf'(1)‎，则f'(2)=(  )‎ A. 1 B. 2 C. 4 D. 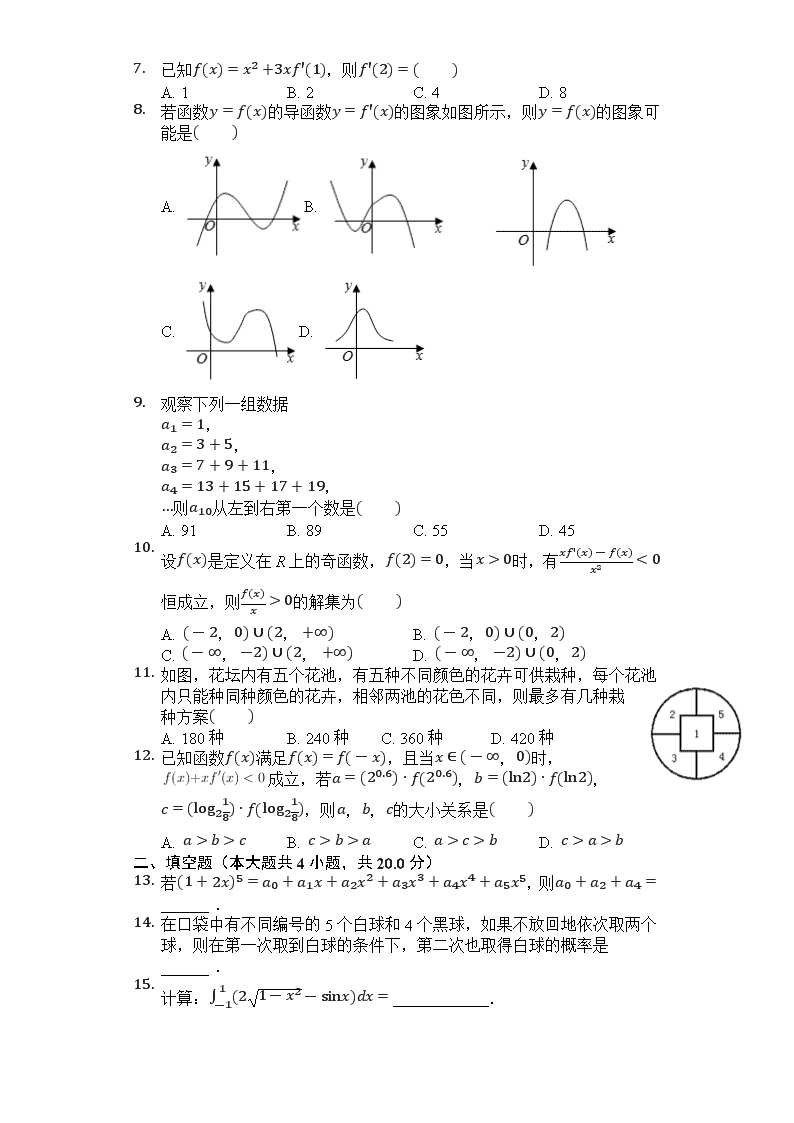8‎ 2. 若函数y=f(x)‎的导函数y=f'(x)‎的图象如图所示，则y=f(x)‎的图象可能是‎(  )‎ A. B. C. D. ‎ 3. 观察下列一组数据 a‎1‎‎=1‎， a‎2‎‎=3+5‎， a‎3‎‎=7+9+11‎， a‎4‎‎=13+15+17+19‎， ‎… ‎则a‎10‎从左到右第一个数是‎(  )‎ A. 91 B. 89 C. 55 D. 45‎ 4. 设f(x)‎是定义在R上的奇函数，f(2)=0‎，当x>0‎时，有xf'(x)-f(x)‎x‎2‎‎<0‎恒成立，则f(x)‎x‎>0‎的解集为‎(  )‎ A. ‎(-2，0)∪(2，+∞)‎ B. ‎(-2，0)∪(0，2)‎ C. ‎(-∞，-2)∪(2，+∞)‎ D. ‎‎(-∞，-2)∪(0，2)‎ 5. 如图，花坛内有五个花池，有五种不同颜色的花卉可供栽种，每个花池内只能种同种颜色的花卉，相邻两池的花色不同，则最多有几种栽种方案‎(  )‎ A. 180种 B. 240种 C. 360种 D. 420种 6. 已知函数f(x)‎满足f(x)=f(-x)‎，且当x∈(-∞，0)‎时，成立，若a=(‎2‎‎0.6‎)⋅f(‎2‎‎0.6‎)，b=(ln2)⋅f(ln2)，c=(log‎2‎‎1‎‎8‎)⋅f(log‎2‎‎1‎‎8‎)‎，则a，b，c的大小关系是‎(  )‎ A. a>b>c B. c>b>a C. a>c>b D. ‎c>a>b 二、填空题（本大题共4小题，共20.0分）‎ 7. 若‎(1+2x‎)‎‎5‎=a‎0‎+a‎1‎x+a‎2‎x‎2‎+a‎3‎x‎3‎+a‎4‎x‎4‎+‎a‎5‎x‎5‎，则a‎0‎‎+a‎2‎+a‎4‎=‎ ______ ．‎ 8. 在口袋中有不同编号的5个白球和4个黑球，如果不放回地依次取两个球，则在第一次取到白球的条件下，第二次也取得白球的概率是______ ．‎ 9. 计算：‎-1‎‎1‎‎(‎‎2‎1-‎x‎2‎-sinx)dx=‎____________．‎ 1. 已知边长分别为a，b，c的三角形ABC面积为S，内切圆O的半径为r，连接OA，OB，OC，则三角形OAB，OBC，OAC的面积分别为‎1‎‎2‎cr，‎1‎‎2‎ar，‎1‎‎2‎br，由S=‎1‎‎2‎cr+‎1‎‎2‎ar+‎1‎‎2‎br得r=‎‎2Sa+b+c，类比得四面体的体积为V，四个面的面积分别为S‎1‎‎，S‎2‎，S‎3‎，‎S‎4‎，则内切球的半径R=‎ ______ ．‎ 三、解答题（本大题共6小题，共72.0分）‎ 2. 某次文艺晚会上共演出8个节目，其中2个唱歌、3个舞蹈、3个曲艺节目，求分别满足下列条件的排节目单的方法种数： ‎(1)‎一个唱歌节目开头，另一个压台； ‎(2)‎两个唱歌节目不相邻； ‎(3)‎两个唱歌节目相邻且3个舞蹈节目不相邻． ‎ 3. 已知函数f(x)=x‎3‎+ax‎2‎+bx(a，b∈R).‎若函数f(x)‎在x=1‎处有极值‎-4‎． ‎(1)‎求f(x)‎的单调递减区间； ‎(2)‎求函数f(x)‎在‎[-1，2]‎上的最大值和最小值． ‎ 4. 已知‎(2x+‎‎1‎x‎)‎n展开式前三项的二项式系数和为22． ‎(‎Ⅰ‎)‎求n的值； ‎(‎Ⅱ‎)‎ 求展开式中的常数项； ‎(III)‎求展开式中二项式系数最大的项． ‎ 1. 在直三棱柱ABC-‎A‎1‎B‎1‎C‎1‎中，底面‎△ABC是直角三角形，AC=BC=AA‎1‎=2，D为侧棱AA‎1‎的中点． ‎(1)‎求异面直线DC‎1‎，B‎1‎C所成角的余弦值； ‎(2)‎求二面角B‎1‎‎-DC-‎C‎1‎的平面角的余弦值．‎ 2. 某地区有800名学员参加交通法规考试，考试成绩的频率分布直方图如图所示‎.‎其中成绩分组区间是：‎[75，80)，[80，85)，[85，90)，[90，95)，[95，100].‎规定90分及其以上为合格． ‎(‎Ⅰ‎)‎求图中a的值 ‎(‎Ⅱ‎)‎根据频率分布直方图估计该地区学员交通法规考试合格的概率； ‎(‎Ⅲ‎)‎若三个人参加交通法规考试，用X表示这三人中考试合格的人数，求X的分布列与数学期望．‎ 3. 已知函数f(x)=a⋅‎exx(a∈R，a≠0)‎． ‎(‎Ⅰ‎)‎当a=1‎时，求曲线f(x)‎在点‎(1，f(1))‎处切线的方程； ‎(‎Ⅱ‎)‎求函数f(x)‎的单调区间； ‎(‎Ⅲ‎)‎当x∈(0，+∞)‎时，若f(x)≥1‎恒成立，求a的取值范围． ‎ ‎ ‎ 答案和解析 ‎【答案】‎ ‎1. B 2. B 3. A 4. D 5. D 6. B 7. A 8. C 9. A 10. B 11. D 12. B ‎ ‎13. 121  ‎ ‎14. ‎1‎‎2‎  ‎ ‎15. π  ‎ ‎16. ‎3VS‎1‎‎+S‎2‎+S‎3‎+‎S‎4‎  ‎ ‎17. 解：‎(1)‎先排歌曲节目有A‎2‎‎2‎种排法，再排其他节目有A‎6‎‎6‎种排法，所以共有A‎2‎‎2‎A‎6‎‎6‎‎=1440‎种排法． ‎(2)‎先排3个舞蹈节目，3个曲艺节目，有A‎6‎‎6‎种排法，再从其中7个空‎(‎包括两端‎)‎中选2个排歌曲节目，有A‎7‎‎2‎种插入方法，所以共有A‎6‎‎6‎A‎7‎‎2‎‎=30240‎种排法． ‎(3)‎两个唱歌节目相邻，用捆绑法，3个舞蹈节目不相邻，利用插空法，共有A‎4‎‎4‎A‎5‎‎3‎A‎2‎‎2‎‎=2880‎种．  ‎ ‎18. 解：‎(1)f'(x)=3x‎2‎+2ax+b，依题意有f'(1)=0，f(1)=-4‎， 即‎3+2a+b=0‎‎1+a+b=-4‎得a=2‎b=-7‎． 所以f'(x)=3x‎2‎+4x-7=(3x+7)(x-1)‎， 由f'(x)<0‎，得‎-‎7‎‎3‎=DC‎1‎⋅‎B‎1‎C‎|DC‎1‎||B‎1‎C|‎=‎-2‎‎5‎‎×‎‎8‎=-‎‎10‎‎10‎． 即异面直线DC‎1‎与B‎1‎C所成角的余弦值为‎10‎‎10‎． ‎(2)‎因为CB‎=(0，2，0)，CA=(2，0，0)，CC‎1‎=(0，0，2)‎， 所以CB‎⋅CA=0，CB⋅CC‎1‎=0‎， 所以CB为平面ACC‎1‎A‎1‎的一个法向量‎.‎          因为B‎1‎C‎=(0，-2，-2)，CD=(2，0，1)‎， 设平面B‎1‎DC的一个法向量为n，n=(x，y，z)‎． 由n⋅B‎1‎C=0‎n⋅CD=0‎，得‎-2y-2z=0‎‎2x+z=0‎ 令x=1‎，则y=2，z=-2，n=(1，2，-2)‎． 所以cos=n⋅‎CB‎|n|⋅|CB|‎=‎4‎‎3×2‎=‎‎2‎‎3‎． 所以二面角B‎1‎‎-DC-‎C‎1‎的余弦值为‎2‎‎3‎．  ‎ ‎21. 解：‎(I)‎由直方图知‎.(0.01+0.02+0.06+0.07+a)×5=1‎． 解得a=0.04‎． ‎(‎Ⅱ‎)‎设事件A为“某名学员交通考试合格”． 由直方图知，P(A)=(0.06+0.02)×5=0.4‎． ‎(III)‎以题意得出X的取值为‎0，1，2，3‎． P(X=0)=(1-0.4‎)‎‎3‎=0.216‎． P(X=1)=C‎3‎‎ ‎1×0.4×(0.6‎)‎‎2‎=0.432‎． P(X=2)=C‎3‎‎2‎×(0.4‎)‎‎2‎×(0.6)=0.288‎． P(X=3)=C‎3‎‎3‎×(0.4‎)‎‎3‎=0.064‎． 所以X的分布列为 ‎ X ‎ 0‎ ‎ 1‎ ‎ 2‎ ‎ 3‎ ‎ P ‎ ‎‎0.216‎ ‎ ‎‎0.432‎ ‎ ‎‎0.288‎ ‎0.064‎ E(X)=0×0.216+1×0.432×2×0.288+3×0.064=1.2‎‎．  ‎ ‎22. 解：‎(‎Ⅰ‎)‎由f(x)=‎a⋅‎exx，得： f'(x)=ax⋅ex-aexx‎2‎=aex(x-1)‎x‎2‎，x≠0‎． 当a=1‎时，f'(x)=‎ex‎(x-1)‎x‎2‎．‎ ‎ 依题意，即在x=1‎处切线的斜率为0． 把x=1‎代入f(x)=‎exx中，得f(1)=e． 则曲线f(x)‎在x=1‎处切线的方程为y=e． ‎(‎Ⅱ‎)‎函数f(x)‎的定义域为‎{x|x≠0}‎． 由于f'(x)=ax⋅ex-aexx‎2‎=‎aex(x-1)‎x‎2‎． ‎①‎若a>0‎， 当x>1‎时，f'(x)>0‎，函数f(x)‎为增函数； 当x<0‎和‎00‎，函数f(x)‎为增函数； 当x>1‎时，f'(x)<0‎，函数f(x)‎为减函数． 综上所述，a>0‎时，函数f(x)‎的单调增区间为‎(1，+∞)‎；单调减区间为‎(-∞，0)，(0，1)‎． a<0‎时，函数f(x)‎的单调增区间为‎(-∞，0)，(0，1)‎；单调减区间为‎(1，+∞)‎． ‎(‎Ⅲ‎)‎当x∈(0，+∞)‎时，要使f(x)=a⋅‎exx≥1‎恒成立， 即使a≥‎xex在x∈(0，+∞)‎时恒成立． 设g(x)=‎xex，则g'(x)=‎‎1-xex． 可知在‎00，g(x)‎为增函数； x>1‎时，g'(x)<0，g(x)‎为减函数． 则g(x‎)‎max=g(1)=‎‎1‎e． 从而a≥‎‎1‎e．  ‎ ‎【解析】‎ ‎1. 解：‎1+i‎-2i‎=‎(1+i)i‎-2‎i‎2‎=-‎1‎‎2‎+‎1‎‎2‎i． 故选：B． 直接利用复数代数形式的乘除运算化简得答案． 本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．‎ ‎2. 解：‎∵f(x)=x‎3‎+x ‎∴f'(x)=3x‎2‎+1 ‎‎∴‎容易求出切线的斜率为4 当x=1‎时，f(x)=2‎ 利用点斜式，求出切线方程为‎4x-y-2=0‎ 故选B． 首先求出函数f(x)‎在点x=1‎处的导数，也就是切线的斜率，再利用点斜式求出切线方程． 本题比较简单，主要应用导数的几何意义，求出切线方程．‎ ‎3. 解：复数i‎3‎‎2i-1‎‎=i‎1-2i=i(1+2i)‎‎(1-2i)(1+2i)‎=-‎2‎‎5‎+‎1‎‎5‎i． 复数i‎3‎‎2i-1‎‎(i为虚数单位‎)‎的共轭复数是：‎-‎2‎‎5‎-‎1‎‎5‎i． 故选：D． 利用复数的除法运算法则化简复数，求解即可． 本题考查复数的基本运算，复数的基本概念，考查计算能力．‎ ‎4. 解：因为‎1‎a‎(‎‎2x+‎1‎x)dx=3+ln2‎， 所以‎(x‎2‎+lnx)|‎ ‎‎1‎a=a‎2‎-1+lna=3+ln2‎，所以a=2‎； 故选D． 将等式左边计算定积分，然后解出a． 本题考查了定积分的计算；关键是正确找出被积函数的原函数．‎ ‎5. 解：‎∵(1-i)(a+i)=1+a+(1-a)i为纯虚数， ‎∴‎‎1+a=0‎‎1-a≠0‎，解得：a=-1‎． 故选：D． 直接由复数代数形式的乘法运算化简‎(1-i)(a+i)‎，再由已知条件列出方程组，求解即可得答案． 本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．‎ ‎6. 解：函数f(x)=‎exx的定义域为：x≠0，x∈R，当x>0‎时，函数f'(x)=‎xex-‎exx‎2‎，可得函数的极值点为：x=1‎，当x∈(0，1)‎时，函数是减函数，x>1‎时，函数是增函数，并且f(x)>0‎，选项B、D满足题意． 当x<0‎时，函数f(x)=exx<0‎，选项D不正确，选项B正确． 故选：B． 利用函数的导数判断函数的单调性以及函数的值域，判断函数的图象即可． 本题考查函数的导数的应用，判断函数的单调性以及函数的图象的判断，考查计算能力．‎ ‎7. 【分析】‎ 本题考查函数与导数，求导公式的应用及函数值求解‎.‎本题求出f'(1)‎是关键步骤．‎ 先求出，令x=1‎，求出f'(1)‎后，导函数即可确定，再求． 【解答】‎ 解：，令x=1‎，得， ‎∴f'(x)=2x-3‎． ． 故选A．‎ ‎8. 解：由y=f'(x)‎可得y=f'(x)‎有两个零点，x‎1‎‎，‎x‎2‎，且‎0‎x‎2‎时，f'(x)<0‎，即函数为减函数， 当x‎1‎‎0‎，函数为增函数， 即当x=‎x‎1‎，函数取得极小值，当x=‎x‎2‎，函数取得极大值， 故选：C 根据函数单调性和导数之间的关系判断函数的单调性即可． 本题主要考查函数图象的判断，结合函数单调性，极值和导数之间的关系是解决本题的关键．‎ ‎9. 解：观察数列‎{an}‎ 中，a‎1‎‎=1，a‎2‎=3+5，a‎3‎=7+9+11，a‎4‎=13+15+17+19，…‎， 各组和式的第一个数为：‎1，3，7，13，…‎ 即 ‎1，1+2，1+2+2×2，1+2+2×2+2×3，…‎‎， 其第n项为：‎1+2+2×2+2×3+…+2×(n-1)‎． ‎∴‎第10项为：‎1+2+2×2+2×3+…+2×9=1+2×‎(1+9)×9‎‎2‎=91‎． 从而a‎10‎的第一个加数为91． 故选A． 观察数列‎{an}‎ 中，各组和式的第一个数：‎1，3，7，13，…‎找出其规律，从而得出a‎10‎的第一个加数为91． 本小题主要考查归纳推理、等差数列求和公式的应用等基础知识，考查运算求解能力，考查分析问题和解决问题的能力‎.‎属于中档题．‎ ‎10. 解：设g(x)=f(x)‎x，f(x)‎是R上的奇函数，‎∴g(x)‎为偶函数； x>0‎时，g'(x)=xf'(x)-f(x)‎x‎2‎<0‎； ‎∴g(x)‎在‎(0，+∞)‎上单调递减，g(2)=0‎； ‎∴‎由g(x)>0‎得，g(x)>g(2)‎； ‎∴g(|x|)>g(2)‎； ‎∴|x|<2‎，且x≠0‎； ‎∴-20‎的解集为‎(-2，0)∪(0，2)‎． 故选：B． 可设g(x)=‎f(x)‎x，根据条件可以判断g(x)‎为偶函数，并可得到x>0‎时，g'(x)<0‎，从而得出g(x)‎在‎(0，+∞)‎上单调递减，并且g(2)=0‎，从而由g(x)>g(2)‎便可得到‎|x|<2‎，且x≠0‎，这样即可得出原不等式的解集． 考查奇函数、偶函数的定义，根据导数符号判断函数单调性的方法，根据函数单调性解不等式的方法，知道偶函数g(x)>g(2)‎等价于g(|x|)>g(2)‎．‎ ‎11. 解：若5个花池栽了5种颜色的花卉，方法有A‎5‎‎5‎种， 若5个花池栽了4种颜色的花卉，则2、4两个花池栽同一种颜色的花； 或者3、5两个花池栽同一种颜色的花，方法有‎2‎A‎5‎‎4‎种， 若5个花池栽了3种颜色的花卉，方法有A‎5‎‎3‎种， 故最多有A‎5‎‎5‎‎+2A‎5‎‎4‎+A‎5‎‎3‎=420‎种栽种方案， 故选D． 若5个花池栽了5种颜色的花卉，方法有A‎5‎‎5‎种，若5个花池栽了4种颜色的花卉，方法有‎2‎A‎5‎‎4‎种，若5个花池栽了3种颜色的花卉，方法有A‎5‎‎3‎种，相加即得所求． 本题主要考查排列、组合以及简单计数原理的应用，体现了分类讨论的数学思想，属于中档题．‎ ‎12. 解：根据题意，令h(x)=xf(x)‎， h(-x)=(-x)f(-x)=-xf(x)=-h(x)‎，则h(x)‎为奇函数； 当x∈(-∞，0)‎时，，则h(x)‎在‎(-∞，0)‎上为减函数， 又由函数h(x)‎为奇函数，则h(x)‎在‎(0，+∞)‎上为减函数， a=(‎2‎‎0.6‎)⋅f(‎2‎‎0.6‎)=h(‎2‎‎0.6‎)，b=(ln2)⋅f(ln2)=h(ln2)，c=(log‎2‎‎1‎‎8‎)⋅f(log‎2‎‎1‎‎8‎)=h(log‎2‎‎1‎‎8‎)=h(-3)‎， 因为log‎2‎‎1‎‎8‎‎<0a>b； 故选：B． 根据题意，构造函数h(x)=xf(x)‎，则a=h(‎2‎‎0.6‎)，b=h(ln2)，c=(log‎2‎‎1‎‎8‎)⋅f(log‎2‎‎1‎‎8‎)=h(-3)‎ ‎，分析可得h(x)‎为奇函数且在‎(-∞，0)‎上为减函数，进而分析可得h(x)‎在‎(0，+∞)‎上为减函数，分析有log‎2‎‎1‎‎8‎‎<00‎和a<0‎分别求出函数的增区间和减区间； ‎(‎Ⅲ‎)‎当x∈(0，+∞)‎时，f(x)≥1‎恒成立，等价于a≥‎xex在x∈(0，+∞)‎时恒成立‎.‎构造辅助函数 g(x)=‎xex，由导数求出函数g(x)‎的最大值，则a的取值范围可求． 本题考查了利用导数研究曲线上某点处的切线方程，考查了利用导数研究函数的单调性，训练了利用分离变量法求参数的取值范围，构造函数并用导数求其最值是解答‎(‎Ⅲ‎)‎的关键，是压轴题．‎