专题05+考前必做基础30题-2017年高考数学（文）走出题海之黄金30题系列（通用版）

专题05+考前必做基础30题-2017年高考数学（文）走出题海之黄金30题系列（通用版）

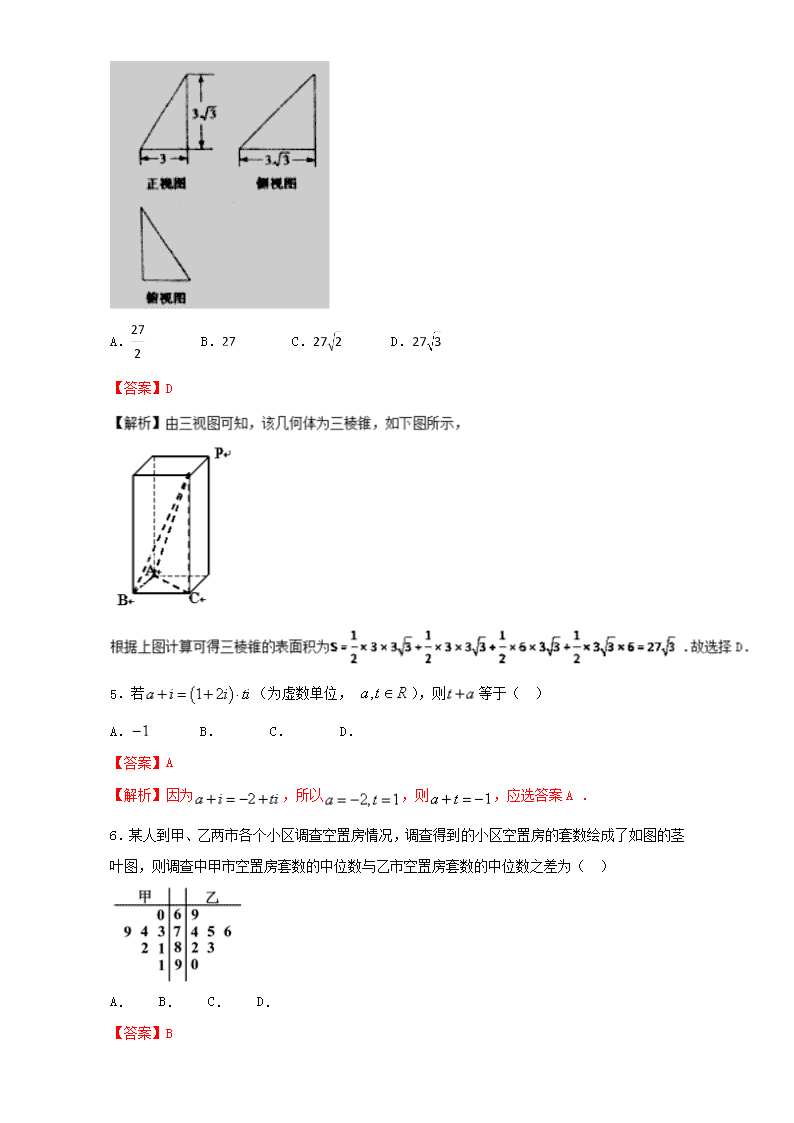
‎2017年高考数学走出题海之黄金系列05‎ ‎1．已知集合，则（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】集合，，所以，故选择B．‎ ‎2．设变量，满足约束条件则目标函数的最大值为（ ）‎ A．6 B． C．0 D．12‎ ‎【答案】A ‎ 3．已知抛物线上一点纵坐标为，则点到抛物线焦点的距离为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】抛物线的准线方程为，点到准线的距离为5，根据抛物线定义可知点到焦点的距离为5．故选择C．‎ ‎4．已知某几何体的三视图如图所示，则该几何体的表面积为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎5．若（为虚数单位， ），则等于（ ）‎ A． B． C． D． ‎ ‎【答案】A ‎ ‎【解析】因为，所以，则，应选答案A ．‎ ‎6．某人到甲、乙两市各个小区调查空置房情况，调查得到的小区空置房的套数绘成了如图的茎叶图，则调查中甲市空置房套数的中位数与乙市空置房套数的中位数之差为（ ）‎ A． B． C． D． ‎ ‎【答案】B ‎【解析】由茎叶图可以看出甲乙两市的空置房的套数的中位数分别是，因此其差是，应选答案B．‎ ‎7．命题“，”的否定是（ ）‎ A． ， B． ，‎ C． ， D． ， ‎ ‎【答案】C ‎8．执行如右图程序框图，输出的为（ ）‎ A． B． C． D． ‎ ‎【答案】A ‎9．已知向量，且，那么的值为（ ）‎ A． B． C． D． ‎ ‎【答案】C ‎【解析】，所以，故选择C．‎ ‎10．若复数满足，则的虚部为（ ）‎ A． B． C． D． ‎ ‎【答案】D ‎【解析】设，，‎ ‎∴，解得．‎ ‎11．已知集合，则（ ）‎ A． B． C． D． ‎ ‎【答案】B ‎【解析】由题可得．‎ ‎12．从含有质地均匀且大小相同的2个红球、个白球的口袋中随机取出一球，若取到红球的概率是，则取得白球的概率等于 （ ）‎ A． B． C． D． ‎ ‎【答案】C ‎【解析】取到红球与取得白球为对立事件， ．‎ ‎13．在平面直角坐标系中，双曲线的一个焦点为 ‎，一条渐近线的倾斜角为60°，则的标准方程为（ ）‎ A． B． C． D． ‎ ‎【答案】C ‎14．若等比数列的前项和，则（ ）‎ A． 4 B． 8 C． 16 D． 32‎ ‎【答案】C ‎【解析】由已知为等比数列， ‎ ‎15．执行如图所示的程序框图，若输入的的值分别为2，2，4，则输出的值是（ ）‎ A． 4 B． 5 C． 6 D． 7‎ ‎【答案】B ‎16．已知，，则等于（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】因为， ，所以，．故选C．‎ ‎17．若， ， ，则大小关系为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎18．如果执行下面的程序框图，且输入， ，则输出的（ ）‎ A． 6 B． 24 C． 120 D． 720‎ ‎【答案】B ‎【解析】第一次循环，可得，第二次循环，可得，‎ 第三次循环，可得，退出循环体，输出．故选B．‎ ‎19．__________．‎ ‎【答案】‎ ‎【解析】 ．‎ ‎20．已知向量，，若，则实数等于_________．‎ ‎【答案】‎ ‎【解析】 ，整理为，故填7．‎ ‎21．已知三内角对应的边长分别为，且，又边长，那么_______．‎ ‎【答案】‎ ‎【解析】根据正弦定理变形，所以．‎ ‎22．小明忘记了微信登陆密码的后两位，只记得最后一位是字母中的一个，另一位是数字4，5，6中的一个，则小明输入一次密码能够成功登陆的概率是__________．‎ ‎【答案】‎ ‎23．已知函数．‎ ‎（Ⅰ）求函数的递增区间；‎ ‎（Ⅱ）的角所对边分别是，角的平分线交于， ，‎ ‎，求．‎ ‎【答案】（1）递增区间是；（2）‎ ‎【解析】（Ⅰ）‎ ‎ ‎ 令，解得，‎ 所以递增区间是； ‎ ‎24．已知四棱锥中，底面是边长为的菱形，，，点是棱的中点，点在棱上，且， //平面．‎ ‎（Ⅰ）求实数的值；‎ ‎（Ⅱ）求三棱锥的体积．‎ ‎【答案】（1）（2）‎ ‎【解析】（Ⅰ）连接，设，则平面平面，‎ ‎//平面， // ， ‎ ‎∽， ，‎ ‎， ． ‎ ‎（Ⅱ），‎ 又 ，‎ ‎， ， ‎ 平面， ‎ 所以．‎ ‎25．在等差数列中， ．‎ ‎（1）求数列的通项；‎ ‎（2）若，求数列的前项和．‎ ‎【答案】(1) ;(2) ．‎ ‎26．在平面直角坐标系中，直线的参数方程为（为参数），圆的方程为．以为极点，轴正半轴为极轴建立极坐标系．‎ ‎（1）求的普通方程与的极坐标方程；‎ ‎（2）已知与交于，求．‎ ‎【答案】（1）（2）‎ ‎27．如图，三棱柱中， ， ， ， ‎ 平面．‎ ‎（1）求证： ；‎ ‎（2）若，求四棱锥的体积．‎ ‎【答案】(Ⅰ）见解析；（Ⅱ） ．‎ ‎28．为了解某地区某种农产品的年产量（单位：吨）对价格（单位：千元/吨）和利润的影响，对近五年该农产品的年产量和价格统计如表：‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎7．0‎ ‎6．5‎ ‎5．5‎ ‎3．8‎ ‎2．2‎ ‎（Ⅰ）求关于的线性回归方程；‎ ‎（Ⅱ）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少时，年利润取到最大值？（保留两位小数）‎ 参考公式：，‎ ‎【答案】(1) ;(2) ．‎ ‎【解析】（Ⅰ），，‎ ‎， ，‎ ‎∴，‎ ‎，所以关于的线性回归方程是．‎ ‎（Ⅱ）年利润，所以当时，年利润最大．‎ ‎29．如图，在长方体中，，，点是线段中点．‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）求点到平面的距离．‎ ‎【答案】(1)详见解析;(2) ．‎ ‎30．为了丰富退休生活，老王坚持每天健步走，并用计步器记录每天健步走的步数．他从某月中随机抽取20天的健步走步数（老王每天健步走的步数都在之间，单位：千步），绘制出频率分布直方图（不完整）如图所示．‎ ‎（1）完成频率分布直方图，并估计该月老王每天健步走的平均步数(每组数据可用区间中点值代替；‎ ‎（2）某健康组织对健步走步数的评价标准如下表:‎ 每天步数分组(千步)‎ 评价级别 及格 良好 优秀 现从这20天中评价级别是“及格”或“良好”的天数里随机抽取2天，求这2天的健步走结果属于同一评价级别的概率．‎ ‎【答案】（1）见解析;（2）．‎ 所抽取的2天属于同一评价级别的结果共4种：．‎ 所以，从这20天中评价级别是“及格”和“良好”的天数里随机抽取2天，‎ 属于同一评价级别的概率．‎