- 2021-04-16 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2021届一轮复习人教A版导数求凹凸性学案
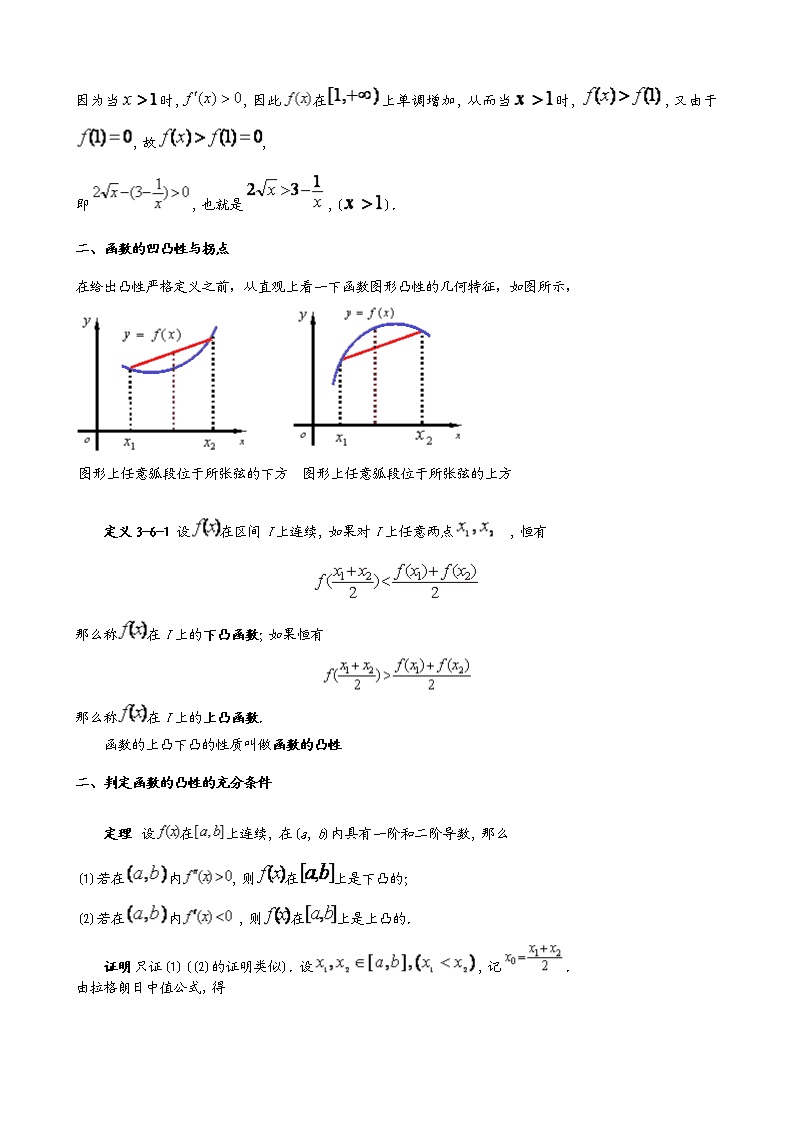
第四节 函数的单调性与曲线的凹凸性 一、函数单调性的判定方法 如果函数在上单调增加(单调减少), 那么它的图形是一条沿轴正向上升(下降)的曲线. 这时曲线的各点处的切线斜率是非负的(是非正的), 即 (或) 由此可见, 函数的单调性与导数的符号有着密切的关系. 反过来, 能否用导数的符号来判定函数的单调性呢? 定理 (函数单调性的判定法) 设函数在上连续, 在内可导. (1)如果在内, 那么函数在上单调增加; (2)如果在内, 那么函数在上单调减少. 证明 只证(1)((2)可类似证得) 在上任取两点, 应用拉格朗日中值定理, 得到 . 由于在上式中, 因此, 如果在内导数保持正号, 即, 那么也有, 于是 从而,因此函数在上单调增加. 证毕 例3-19 判定函数在上的单调性. 解 因为在内, 所以由判定法可知函数在上单调增加. 例3-20 讨论函数的单调性. 解 由于 且函数的定义域为 令, 得, 因为在内, 所以函数在上单调减少; 又在内, 所以函数在上单调增加. 例3-21 讨论函数的单调性. 解: 显然函数的定义域为, 而函数的导数为 所以函数在处不可导. 又因为时,, 所以函数在上单调减少; 因为时, , 所以函数在上单调增加. 说明: 如果函数在定义区间上连续, 除去有限个导数不存在的点外导数存在且连续, 那么只要用方程的根及导数不存在的点来划分函数的定义区间, 就能保证在各个部分区间内保持固定的符号, 因而函数在每个部分区间上单调. 例3-22. 确定函数的单调区间. 解 该函数的定义域为. 而,令, 得. 列表 + - + ↗ ↘ ↗ 函数f(x)在区间和内单调增加, 在区间上单调减少. 例3-23讨论函数的单调性. 解 函数的定义域为 函数的导数为:, 除时, 外, 在其余各点处均有 因此函数在区间上单调减少; 因为当时, , 所以函数在及上都是单调增加的. 从而在整个定义域内是单调增加的.其在处曲线有一水平切线. 说明:一般地, 如果在某区间内的有限个点处为零, 在其余各点处均为正(或负)时, 那么在该区间上仍旧是单调增加(或单调减少)的. 例3-24 证明: 当时, . 证明: 令, 则 因为当时,, 因此在上单调增加, 从而当时, ,又由于, 故, 即, 也就是,(). 二、函数的凹凸性与拐点 在给出凸性严格定义之前,从直观上看一下函数图形凸性的几何特征,如图所示, 图形上任意弧段位于所张弦的下方 图形上任意弧段位于所张弦的上方 定义3-6-1 设在区间I上连续, 如果对I上任意两点 , 恒有 那么称在I上的下凸函数; 如果恒有 那么称在I上的上凸函数. 函数的上凸下凸的性质叫做函数的凸性 二、判定函数的凸性的充分条件 定理 设在上连续, 在(a, b)内具有一阶和二阶导数, 那么 (1)若在内, 则在上是下凸的; (2)若在内 , 则在上是上凸的. 证明 只证(1)((2)的证明类似). 设, 记. 由拉格朗日中值公式, 得 , , 两式相加并应用拉格朗日中值公式得 , 即, 所以在上的图形是凹的. 拐点: 连续曲线上凸与下凸的分界点称为这曲线的拐点. 确定曲线的凹凸区间和拐点的步骤: (1)确定函数的定义域; (2)求出在二阶导数 ; (3)求使二阶导数为零的点和使二阶导数不存在的点; (4)判断或列表判断, 确定出曲线凹凸区间和拐点; 注: 根据具体情况(1)、(3)步有时省略. 例3-34 判断曲线的凸性. 解: 因为 , . 令 得, 当时, , 所以曲线在内为上凸的; 当时,, 所以曲线在内为下凸的. 例3-35 求曲线的拐点及凸性区间. 解: (1)函数的定义域为; (2) ,;(3)解方程, 得, ; (4)列表判断: 在区间和上曲线是下凸的, 在区间上曲线是上凸的. 点 和是曲线的拐点. 例3-36 问曲线是否有拐点? 解 , . 当时, , 在区间内曲线是下凸的, 因此曲线无拐点. 例3-37 求曲线的拐点. 解 (1)函数的定义域为; (2) , ; (3)函数无二阶导数为零的点,二阶导数不存在的点为 ; (4)判断: 当时,; 当时, 因此, 点是曲线的拐点. 拉格朗日中值定理: 如果函数f(x)在(a,b)上可导,[a,b]上连续,则必有一ξ∈[a,b]使得f'(ξ)*(b-a)=f(b)-f(a) 示意图 令f(x)为y,所以该公式可写成△y=f'(x+θ△x)*△x (0<θ<1) 上式给出了自变量取得的有限增量△x时,函数增量△y的准确表达式,因此本定理也叫有限增量定理。查看更多