人教版必修二5.4《圆周运动》WORD教案3

人教版必修二5.4《圆周运动》WORD教案3

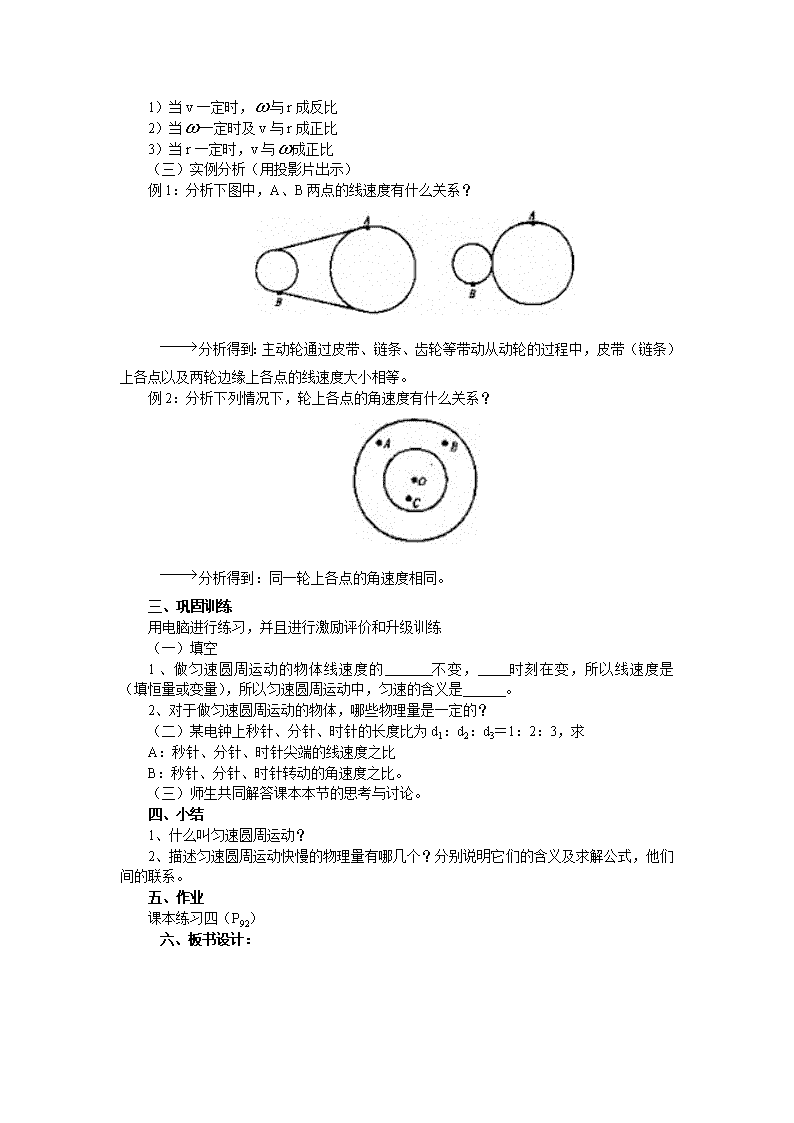
第四节 匀速圆周运动 ‎ 教学目标：‎ ‎ 一、知识目标：‎ ‎ 1、知道什么是匀速圆周运动 ‎ 2、理解什么是线速度、角速度和周期 ‎ 3、理解线速度、角速度和周期之间的关系 ‎ 二、能力目标：‎ ‎ 能够匀速圆周运动的有关公式分析和解决有关问题。‎ ‎ 三、德育目标：‎ ‎ 通过描述匀速圆周运动快慢的教学，使学生了解对于同一个问题可以从不同的侧面进行研究。‎ ‎ 教学重点：‎ ‎ 1、理解线速度、角速度和周期 ‎ 2、什么是匀速圆周运动 ‎ 3、线速度、角速度及周期之间的关系 ‎ 教学难点：‎ ‎ 对匀速圆周运动是变速运动的理解 ‎ 教学方法：‎ ‎ 讲授、推理归纳法 ‎ 教学用具：‎ ‎ 投影仪、投影片、多媒体 ‎ 教学步骤：‎ ‎ 一、导入新课 ‎ （1）物体的运动轨迹是圆周，这样的运动是很常见的，同学们能举几个例子吗？（例：转动的电风扇上各点的运动，地球和各个行星绕太阳的运动等）‎ ‎ （2）今天我们就来学习最简单的圆周运动——匀速圆周运动 ‎ 二、新课教学 ‎ （一）用投影片出示本节课的学习目标 ‎ 1、理解线速度、角速度的概念 ‎ 2、理解线速度、角速度和周期之间的关系 ‎ 3、理解匀速圆周运动是变速运动 ‎ （二）学习目标完成过程 ‎ 1、匀速圆周运动 ‎ （1）用多媒体投影一个质点做圆周运动，在相等的时间里通过相等的弧长。‎ ‎ （2）并出示定义：质点沿圆周运动，如果在相等的时间里通过的圆弧长度相同——这种运动就叫匀速圆周运动。‎ ‎ （3）举例：通过放录像让学生感知：一个电风扇转动时，其上各点所做的运动，地球和各个行星绕太阳的运动，都认为是匀速圆周运动。‎ ‎ （4）通过电脑模拟：两个物体都做圆周运动，但快慢不同，过渡引入下一问题。‎ ‎ 2、描述匀速圆周运动快慢的物理量 ‎ （1）线速度 ‎ a：分析：物体在做匀速圆周运动时，运动的时间t增大几倍，通过的弧长也增大几倍，所以对于某一匀速圆周运动而言，s与t的比值越大，物体运动得越快。‎ ‎ b：线速度 ‎ 1）线速度是物体做匀速圆周运动的瞬时速度。‎ ‎ 2）线速度是矢量，它既有大小，也有方向。‎ ‎3）线速度的大小 ‎ 4）线速度的方向在圆周各点的切线方向上 ‎ 5）讨论：匀速圆周运动的线速度是不变的吗？‎ ‎ 6）得到：匀速圆周运动是一种非匀速运动，因为线速度的方向在时刻改变。‎ ‎ （2）角速度 ‎ a：学生阅读课文有关内容 ‎ b：出示阅读思考题 ‎ 1）角速度是表示 的物理量 ‎ 2）角速度等于 和 的比值 ‎ 3）角速度的单位是 ‎ ‎ c：说明：对某一确定的匀速圆周运动而言，角速度是恒定的 ‎ d：强调角速度单位的写法rad/s ‎ （3）周期、频率和转速 ‎ a：学生阅读课文有关内容 b：出示阅读思考题：‎ ‎1） 叫周期， 叫频率； 叫转速 ‎ 2）它们分别用什么字母表示？‎ ‎3）它们的单位分别是什么？‎ c阅读结束后，学生自己复述上边思考题。‎ ‎ （4）线速度、角速度、周期之间的关系 ‎ a：过渡：既然线速度、角速度、周期都是用来描述匀速圆周运动快慢的物理量，那么他们之间有什么样的关系呢？‎ ‎ b：用投影片出示思考题 ‎ 一物体做半径为r的匀速圆周运动 ‎ 1）它运动一周所用的时间叫 ，用T表示。它在周期T内转过的弧长为 ，由此可知它的线速度为 。‎ ‎ 2）一个周期T内转过的角度为 ，物体的角速度为 。‎ c：通过思考题总结得到：‎ ‎ ‎ ‎ d：讨论 ‎ 1）当v一定时，与r成反比 ‎ 2）当一定时及v与r成正比 ‎ 3）当r一定时，v与成正比 ‎ （三）实例分析（用投影片出示）‎ ‎ 例1：分析下图中，A、B两点的线速度有什么关系？‎ 分析得到：主动轮通过皮带、链条、齿轮等带动从动轮的过程中，皮带（链条）上各点以及两轮边缘上各点的线速度大小相等。‎ ‎ 例2：分析下列情况下，轮上各点的角速度有什么关系？ ‎ 分析得到：同一轮上各点的角速度相同。‎ ‎ 三、巩固训练 ‎ 用电脑进行练习，并且进行激励评价和升级训练 ‎ （一）填空 ‎ 1、做匀速圆周运动的物体线速度的 不变， 时刻在变，所以线速度是 （填恒量或变量），所以匀速圆周运动中，匀速的含义是 。‎ ‎ 2、对于做匀速圆周运动的物体，哪些物理量是一定的？‎ ‎ （二）某电钟上秒针、分针、时针的长度比为d1：d2：d3＝1：2：3，求 ‎ A：秒针、分针、时针尖端的线速度之比 ‎ B：秒针、分针、时针转动的角速度之比。‎ ‎ （三）师生共同解答课本本节的思考与讨论。‎ ‎ 四、小结 ‎ 1、什么叫匀速圆周运动？‎ ‎ 2、描述匀速圆周运动快慢的物理量有哪几个？分别说明它们的含义及求解公式，他们间的联系。‎ ‎ 五、作业 ‎ 课本练习四（P92）‎ 六、板书设计：‎