知识讲解_匀变速直线运动的位移与时间的关系(基础)

知识讲解_匀变速直线运动的位移与时间的关系(基础)

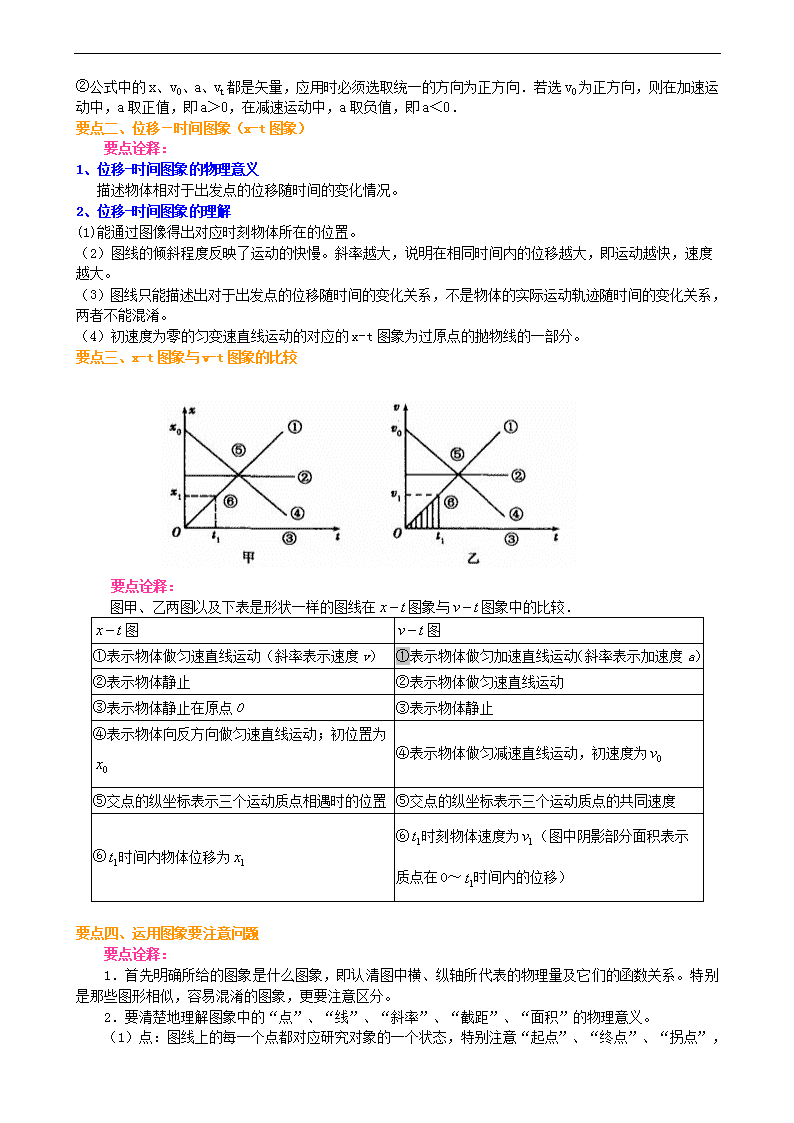
匀变速直线运动的位移与时间的关系 【学习目标】 1、掌握 v -t 图象描述位移的方法 2、掌握位移与时间的关系并能灵活应用 【要点梳理】 要点一、匀变速直线运动的位移公式推导 方法一：用 v-t 图象推导 在匀变速直线运动中，虽然速度时刻变化，但只要时间足够小，速度的变化就非常小，在这段时间内 近似应用我们熟悉的匀速运动的公式计算位移，其误差也非常小，如图所示． 如果把每一小段△t 内的运动看做匀速运动，则矩形面积之和等于各段匀速直线运动的位移，显然小 于匀变速直线运动在该段时间内的位移．但时间越小，各匀速直线运动的位移和与匀变速直线运动的位移 之间的差值就越小，当△t→0 时，各矩形面积之和趋近于 v-t 图线下面的面积．可以想象，如果把整个运 动过程划分得非常非常细，很多很多小矩形的面积之和就能准确代表物体的位移了，位移的大小等于图丙 中梯形的面积． 这一推理及前面讲瞬时速度时，都用到无限分割逐渐逼近的方法，这是微积分原理的基 本思想之一，我们要注意领会． 匀变速直线运动的 v-t 图象与 t 轴所夹面积表示 t 时间内的位移．此结论可推至任何直线运动．图线与 时间轴间的面积表示位移，下方的面积表示负向位移，它们的代数和表示总位移，算术和表示路程．由前 面的讨论可知，当时间间隔分割得足够小时，折线趋近于直线 AP，设想的运动就代表了真实的运动，由 此可以求出匀变速运动在时间 t 内的位移，它在数值上等于直线 AP 下方的梯形 OAPQ 的面积(如图丙)．这 个面积等于 2 1 2 0 1 1 2 2S S S OA OQ AR RP v t at       ， 即位移 2 0 1 2x v t at  ． 这就是匀变速直线运动的位移公式． 方法二：用公式推导 由于位移 x vt ，而 0 2 tv vv  ， 又 0tv v at  ， 故 0 0 2 v v atx t   ， 即 2 0 1 2x v t at  ． 要点诠释： ①该式也是匀变速直线运动的基本公式，和 0tv v at  综合应用，可以解决所有的匀变速直线运动问题． ②公式中的 x、v0、a、vt 都是矢量，应用时必须选取统一的方向为正方向．若选 v0 为正方向，则在加速运 动中，a 取正值，即 a＞0，在减速运动中，a 取负值，即 a＜0． 要点二、位移－时间图象（x-t 图象） 要点诠释： 1、位移-时间图象的物理意义 描述物体相对于出发点的位移随时间的变化情况。 2、位移-时间图象的理解 (1)能通过图像得出对应时刻物体所在的位置。 （2）图线的倾斜程度反映了运动的快慢。斜率越大，说明在相同时间内的位移越大，即运动越快，速度 越大。 （3）图线只能描述出对于出发点的位移随时间的变化关系，不是物体的实际运动轨迹随时间的变化关系， 两者不能混淆。 （4）初速度为零的匀变速直线运动的对应的 x-t 图象为过原点的抛物线的一部分。 要点三、x-t 图象与 v-t 图象的比较 要点诠释： 图甲、乙两图以及下表是形状一样的图线在 x t 图象与 v t 图象中的比较． x t 图 v t 图 ①表示物体做匀速直线运动（斜率表示速度 v） ①表示物体做匀加速直线运动（斜率表示加速度a） ②表示物体静止 ②表示物体做匀速直线运动 ③表示物体静止在原点 O ③表示物体静止 ④表示物体向反方向做匀速直线运动；初位置为 0x ④表示物体做匀减速直线运动，初速度为 0v ⑤交点的纵坐标表示三个运动质点相遇时的位置 ⑤交点的纵坐标表示三个运动质点的共同速度 ⑥ 1t 时间内物体位移为 1x ⑥ 1t 时刻物体速度为 1v（图中阴影部分面积表示质 点在 0～ 1t 时间内的位移） 要点四、运用图象要注意问题 要点诠释： 1．首先明确所给的图象是什么图象，即认清图中横、纵轴所代表的物理量及它们的函数关系。特别 是那些图形相似，容易混淆的图象，更要注意区分。 2．要清楚地理解图象中的“点”、“线”、“斜率”、“截距”、“面积”的物理意义。 （1）点：图线上的每一个点都对应研究对象的一个状态，特别注意“起点”、“终点”、“拐点”， 它们往往对应一个特殊状态。 （2）线：表示研究对象的变化过程和规律，如 v t 图象中图线若为倾斜直线，则表示物体做匀变速 直线运动。 （3）斜率：表示横、纵坐标轴上两物理量的比值，常有一个重要的物理量与之对应。用于定量计算 对应物理量的大小和定性分析变化的快慢问题。如 x t 图象的斜率表示速度大小， v t 图象的斜率表示 加速度大小。 （4）面积：图线与坐标轴围成的面积常与某一表示过程的物理量相对应。如 v t 图象与横轴包围的 “面积”大小表示位移大小。 （5）截距：表示横、纵坐标两物理量在“边界”条件下的物理量的大小。由此往往能得到一个很有 意义的物理量。 【典型例题】 类型一、关于位移图象的理解 例 1、某物体的位移图象如图所示，若规定向东为位移的正方向，试求；物体在 OA、AB、BC、CD、DE 各阶段的速度。 【答案】见解析 【解析】物体在 t＝0 开始从原点出发向东行做匀速直线运动，历时 2s；接着在第 3s～5s 内静止；第 6s 内 继续向东做匀速直线运动；在第 7s～8s 内匀速反向西行，至第 8s 末回到出发点；在第 9s～12s 内从原点 向西行做匀速直线运动。 由 x－t 图得各阶段的速度如下： OA 段： 1 1 1 6 / 3 /2 xv m s m st    ，向东 AB 段：物体静止，速度为 0 BC 段： 3 3 3 12 6 / 6 /1 xv m s m st    ，向东 CD 段： 4 4 4 0 12 / 6 /2 xv m s m st     ，负号说明方向向西 DE 段： 5 5 5 4 0 / 1 /4 xv m s m st      ，向西 【总结升华】位移图象的斜率表示速度的大小和方向（斜率的正负表示速度的方向）。图象平行于 t 轴，说 明物体的速度为零，表示物体静止；图象斜率为正值，表示物体沿与规定方向相同的方向运动；图象斜率 为负值，表示物体沿与规定方向相反的方向运动。 举一反三 【变式】如图所示，A、B 两物体从 O 点开始运动，从 A、B 两物体的位移图象可知，下述说法正确的是( ) A、A、B 两物体的运动方向相同 B、A 物体 2s 内发生的位移是 l0m C、B 物体发生 l0m 的位移的时间是 2s D、A 物体的速度大小是 5m/s，B 的速度大小是 2.5m/s 【答案】ABD 类型二、位移与时间关系公式的应用中注意问题 例 2、列车进站前刹车，已知刹车前列车速度为 60km/h，刹车加速度大小为 0.8m/s2，求刹车后 15s 和 30s 列车的速度． 【答案】4.7m/s 0 【解析】以初速度方向为正方向，60km/h＝16.7m/s，刹车后 15s，列车的速度 1 0v v at   16.7m /s 0.8 15m /s 4.7m /s   ；刹车至列车停下所需时间 0 0 16.7 s 20.9s0.8 tv vt a     ，故刹车后 30s 列车的速度 v2＝0． 【总结升华】解匀减速问题应注意：（1）书写格式规范，如不能写成 v1＝v0-at，因 a 是矢量，代入数字时 带有方向“+”或“-”。“+”可以省去．(2)刹车类问题应注意停止运动的时间，一般应先判断多长时间停 下，再来求解．本题若代入 30s 运算得 v2＝-7.3m/s，是错误的．物理题目的求解结果一定要符合实际， 例如你所求得的量若质量出现负值就是不符合实际的． 举一反三 【变式 1】以 18m/s 的速度行驶的汽车，紧急刹车后做匀减速直线运动，其加速度的大小为 6m/s2，求汽 车在 6s 内通过的距离． 【答案】27m 【解析】如果把 a＝-6m/s2 和 v0＝18m/s 代入位移公式 2 0 1 2x v t at  ，得 2118 6m ( 6) 6 m 02x        ． 汽车在 6 s 内的位移竟然为 0，这可能吗?为什么会出现这样的结果?原来汽车刹车后只运动了 3s，3s 后便停下了，直接把 6s 的时间代入公式必定会出现错误的结论．故应先判断汽车停下的时间，设历时 t0 停下， 0 18 / 3sm st a   ， 06st t  ，故 6s 内的位移等于 3 s 内的位移． 解法一：由 0 0 0 1 2x v t at  ，有 2118 3m ( 6) 3 m 27m2x        ． 解法二：由逆向运动法知， 2 2 0 1 1 6 3 27m2 2x at m     ． 解法三：由 0 02 vx t 有， 18 3m 27m2x    ． 【高清课程：匀变速直线运动中位移与时间的关系 第 5 页】 【变式 2】由静止开始做匀加速直线运动的汽车，第 ls 内通过 0.4m 位移，则不正确的结论是( ) A．第 1s 末的速度的 0.8m/s B．加速度为 0.8m/s2 C．第 2s 内通过位移为 1.2m D．2s 内通过的位移为 1.2m 【答案】D 类型三、位移图象描述相遇问题 例 3、如图所示是做直线运动的甲、乙两物体的 x-t 图象，下列说法中正确的是（ ） A、甲启动的时刻比乙早 t1 B、当 t = t2 时，两物体相遇 C、当 t = t2 时，两物体相距最远 D、 当 t = t3 时，两物体相距 x1 【答案】ABD 【解析】由 x-t 图象可知甲物体是在计时起点从坐标原点 x1 处开始沿 x 负方向做匀速直线运动，乙物体是 在 t1 时刻开始从坐标原点沿 x 正方向做匀速直线运动，两物体在 t2 时刻相遇，然后远离，t3 时刻两物体相 距 x1，因此选项 ABD 正确。 【总结升华】x-t 图象中两图线相交说明两物体相遇，其交点 A 的横坐标表示相遇的时刻，纵坐标表示相 遇处对参考点的位移。 举一反三 【变式 1】如图所示，折线 a 是表示物体甲从 A 地向 B 地运动的位移图线，直线 b 是表示物体乙从 B 地向 A 地运动的位移图线，则下述说法中正确的是（ ） A、甲、乙两物体是相向运动 B、甲物体是匀速运动，速度大小是 7.5m/s C、甲、乙两物体运动 8s 后，在距甲的出发点 60m 处相遇 D、甲在运动中停了 4s 【答案】ACD 【解析】由图象知，甲、乙两物体在开始运动时相距 100m，后来相距越来越小，甲向乙的出发点运动， 乙向甲的出发点运动，因而它们是相向运动，选项 A 正确。 两图线相交点表示了甲、乙同一时刻同一位置，即相遇的时刻与位置，故选项 C 正确。 甲在运动中有一段图线与时间轴平行，这表示甲在 4s 内位置始终没变，因而是静止的，选项 D 正确。 甲在全过程中并不是匀速运动，故选项 B 是错的。 【变式 2】一质点的 x-t 图象如图甲所示，那么此质点的 v-t 图象可能是图乙中的( )． 【答案】A 【解析】解题关键明白两种图象斜率的物理意义不同．v-t 图象的切线斜率表示速度，由图象可知：0～ 1 2 t 时间内图象的斜率为正且越来越小，在 1 2 t 时刻图象斜率为 0，即物体正向速度越来越小， 1 2 t 时刻减为零； 从 1 2 t ～ 1t 时间内，斜率为负值，数值越来越大，即速度反向增大，故选项 A 正确． 类型四、位移公式解决实际问题 例 4、某市规定，汽车在学校门前马路上的行驶速度不得超过 40 km/h．一次，一辆汽车在校门前马路上 遇紧急情况刹车，由于车轮抱死，滑行时在马路上留下一道笔直的车痕．交警测量了车痕长度 x＝9m，又 从监控资料上确定了该车从刹车到停止的时间 t＝1.5s，立即判断出这辆车违章超速，这是为什么? 【答案】汽车超速 【解析】解法一：(速度判断法)由于 x＝9m，t＝1.5 s，据 xv t  得平均速度 9 m /s 6m /s1.5v   ，又因 为 0 2 vv  ，得初速度 0 2v v  2×6m/s＝12m/s＝43.2km/h． 由于车速超过 40 km/h，可知此车超速． 解法二：(位移判断法)设汽车恰以 0 10040km / h m /s9v   的速度行驶，则刹车后 1.5s 停下，刹车 加速度 2 20 100 0 2009 m /s m /s1.5 1.5 27 vva t      ． 以此加速度刹车，刹车位移 2 2 0 1 100 1 2001.5 1.5 m 8.33m 9m2 9 2 27x v t at                  ，故 汽车超速． 【总结升华】超速判断涉及科技生活情景，是高考热点，可用速度判断，即根据刹车的运动矢量判断刹车 前速度与限速关系；也可用位移判断，即假设以限速行驶，在实际刹车情景中的刹车位移与求得的刹车位 移对比，从而判断是否超速． 举一反三 【变式】一辆汽车在笔直的公路上做匀变速直线运动，该公路每隔 15 m 安置一个路标，如图所示，汽车 通过 AB 两相邻路标用了 2s，通过 BC 两路标用了 3s，求汽车通过 A、B、C 三个路标时的速度． 【答案】8.5m/s 6.5m/s 3.5m/s 【解析】题目中已知条件是位移、时间，求的是速度，所以可用位移公式求解． 汽车从 A 到 C 是匀变速直线运动，设汽车通过路标 A 时速度为 vA，通过 AB 的时间 t1＝2s，通过 BC 的时间 t2＝3s．根据位移公式 2 0 1 2x v t at  ，研究 AB 运动的过程，有 2 1 1 1 2AB Ax v t at  ． 研究 AC 运动过程，有 21 2AC Ax v t at  ， 其中 t＝t1+t2＝5s， 解得 vA＝8.5m/s，a＝-1m/s2． 再根据速度公式 vB＝vA+at1＝6.5m/s，vC＝vA+at＝3.5m/s． 求得 a＝-1 m/s2，其中“-”说明 a 的方向与初速的方向相反，汽车做匀减速直线运动． 【高清课程：匀变速直线运动中位移与时间的关系 第 6 页】 【变式 2】两物体从同一地点同时出发，沿同一方向做匀加速直线运动，若它们的初速度大小不同，而加 速度大小相同，则在运动过程中（ ） A．两物体速度之差保持不变 B．两物体的速度之差与时间成正比 C．两物体的位移之差与时间成正比 D．两物体的位移之差与时间的平方成正比 【答案】AC 【高清课程：匀变速直线运动中位移与时间的关系 第 8 页】 【变式 3】一物体以 5m/s 的初速度，－2m/s2 的加速度在粗糙水平面上滑行，4s 内物体通过的位移为（ ） A．4m B．36m C．6.25m D．以上答案都不对 【答案】C 【高清课程：匀变速直线运动中位移与时间的关系 第 10 页】 【变式 4】矿井里的升降机由静止开始匀加速上升，经过 5s 速度达到 v=4 m/s 后，又以这个速度匀速上升 20s，然后匀减速上升，再经 4s 停在井口．求矿井的深度． 【答案】98m