人教版高中数学必修4全册

人教版高中数学必修4全册

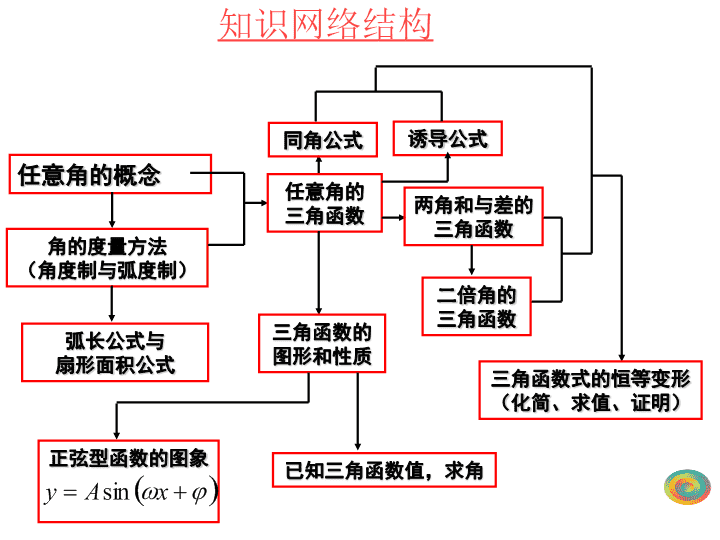
2021年1月20日 高中数学必修 四 课件全册（人教A版） 任意角的概念 角的度量方法 （角度制与弧度制） 弧长公式与 扇形面积公式 任意角的 三角函数 同角公式 诱导公式 两角和与差的三角函数 二倍角的三角函数 三角函数式的恒等变形 （化简、求值、证明） 三角函数的 图形和性质 正弦型函数的图象 已知三角函数值，求角 知识网络结构 1. 角的概念的推广 （ 1 ） 正角，负角和零角 . 用旋转的观点定义角，并规定了旋转的正方向，就出现了正角，负角和零角，这样角的大小就不再限于 0 0 到 360 0 的范围 . （ 3 ） 终边相同的角 ，具有共同的绐边和终边的角叫终边相同的角，所有与角终边相同的角（包含角在内）的集合为 . （ 4 ）角在“到”范围内，指 . （ 2 ） 象限角和轴线角 . 象限角的前提是角的顶点与直角坐标系中的坐标原点重合，始边与轴的非负半轴重合，这样当角的终边在第几象限，就说这个角是第几象限的角，若角的终边与坐标轴重合，这个角不属于任一象限，这时也称该角为轴线角 . 一、基本概念： 一、任意角的三角函数 1 、 角的概念的推广 正角 负角 o x y 的终边 的终边 零角 二、象限角： 注 ：如果角的终边在坐标轴上，则该角不是象限角。 三、所有与角 终边相同的角，连同角 在内，构成集合： （角度制） （弧度制） 例 1 、求在 到 （ ）范围内，与下列各角终边相同的角 原点 x 轴的非负半轴 一、在直角坐标系内讨论角，角的顶点与 重合，角的始边 与 重合。逆时针旋转为正，顺时针旋转为负。 角的终边（除端点外）在第几象限，我们就说这个角是第几象限角。 1 、终边相同的角与相等角的区别 终边相同的角不一定相等，相等的角终边一定相同。 2 、象限角、象间角与区间角的区别 3 、角的终边落在“射线上”、“直线上”及“互相垂直的两条直线上”的一般表示式 三、终边相同的角 (1) 与  角 终边相同的角的集合 : 1. 几类特殊角的表示方法 {  |  =2 k +  , k ∈ Z }. (2) 象限角、象限界角 ( 轴线角 ) ① 象限角 第一象限角 : (2 k  <  <2 k  + , k  Z) 2  第二象限角 : (2 k  + <  <2 k  +  , k  Z) 2  第三象限角 : (2 k  +  <  <2 k  + , k  Z) 2 3  第四象限角 : 2  (2 k  + <  <2 k  +2  , k  Z 或 2 k  - <  <2 k  , k  Z ) 2 3  一、角的基本概念 ② 轴线角 x 轴的非负半轴 :  = k  360º(2 k  )( k  Z); x 轴的非正半轴 :  = k  360º+180º(2 k  +  )( k  Z); y 轴的非负半轴 :  = k  360º+90º(2 k  + )( k  Z); 2  y 轴的非正半轴 :  = k  360º+270º(2 k  + ) 或  = k  360º - 90º(2 k  - )( k  Z); 2 3  2  x 轴 :  = k  180º( k  )( k  Z); y 轴 :  = k  180º+90º( k  + )( k  Z); 2  坐标轴 :  = k  90º( )( k  Z). 2 k  例 2 、（ 1 ）、终边落在 x 轴上的角度集合： （ 2 ）、终边落在 y 轴上的角度集合： （ 3 ）、终边落在象限平分线上的角度集合： 典型例题 各个象限的半角范围可以用下图记忆，图中的 Ⅰ 、 Ⅱ 、 Ⅲ 、 Ⅳ 分别指第一、二、三、四象限角的半角范围； 例 1. 若 α 是第三象限的角，问 α/2 是哪个象限的角 ?2α 是哪个象限的角 ? 高考试题精选及分析 C 点评 : 本题先由 α 所在象限确定 α/2 所在象限 , 再 α/2 的余弦符号确定结论 . 例 1 求经过 1 小时 20 分钟时钟的分针所转过的角度： 解：分针所转过的角度 例 2 已知 a 是第二象限角，判断下列各角是第几象限角 （ 1 ） （ 2 ） 评析： 在解选择题或填空题时， 如求角所在象限，也可以不讨论 k 的 几种情况，如图所示利用图形来判断 . 四、什么是 1 弧度的角？ 长度等于半径长的弧所对的圆心角。 O A B r r 2r O A B r （ 3 ） 角度与弧度的换算 . 只要记住，就可以方便地进行换算 . 应熟记一些特殊角的度数和弧度数 . 在书写时注意不要同时混用角度制和弧度制 （ 4 ） 弧长公式和扇形面积公式 . 度 弧度 0 2 、 角度与弧度的互化 特殊角的角度数与弧度数的对应表 略 解： 例 3 ．已知角  和  满足求角  –  的范围 . 解： 例 4 、 已知扇形的周长为定值 100 ，问扇形的半径和圆心角分别为多少时扇形面积最大？最大值是多少？ 扇形面积最大值为 625. 例 7. 已知一扇形中心角是 α ，所在圆的半径是 R. ① 若 α ＝ 60° ， R ＝ 10cm ，求扇形的弧长及该弧所在的弓形面积 . ② 若扇形的周长是一定值 C ( C ＞ 0) ，当 α 为多少弧度时，该扇形的面积有最大值 ? 并求出这一最大值 ? 指导 : 扇形的弧长和面积计算公式都有角度制和弧度制两种给出的方式，但其中用弧度制给出的形式不仅易记，而且好用 . 在使用时，先要将问题中涉及到的角度换算为弧度 .   解：（ 1 ）设弧长为 l ，弓形面积为 S 弓 。 （ 2 ） 扇形周长 C=2 R + l =2 R + 正弦线： 余弦线： 正切线： （ 2 ）当角 α 的终边在 x 轴上时，正弦线，正切线变成一个点；当角 α 的终边在 y 轴上时，余弦线变成一个点，正切线不存在。 2. 正弦线、余弦线、正切线 x y O P T M A 有向线段 MP 有向线段 OM 有向线段 AT 注意： （ 1 ）圆心在原点，半径为单位长的圆叫单位圆 . 在平面直角坐标系中引进 正弦线、余弦线和正切线 三角函数 三角函数线 正弦函数 余弦函数 正切函数 正弦线 MP 正弦、余弦函数的图象 y x x O -1  P M A(1,0) T sin =MP cos =OM tan =AT 注意： 三角函数线是 有向线段 ！ 余弦线 OM 正切线 AT  P O M  P O M  P O M  P O M MP 为角  的正弦线 , OM 为角  的余弦线 为第二象限角时  为第一象限角时  为第三象限角时  为第四象限角时  10 ） 函数 y=lg sinx+ 的定义域是（ A ） （ A ） {x|2k π0,ω>0) 的图象的对称中心和对称轴方程 2 、函数 的图象（ A>0, >0 ) 第一种变换 : 图象向左 ( ) 或 向右 ( ) 平移 个单位 横坐标伸长 ( ) 或缩短 ( ) 到原来的 倍 纵坐标不变 纵坐标伸长 (A>1 ) 或缩短 ( 01 ) 或缩短 ( 00,|φ|< ) 的图象向左平移 个单位，再数将图象上所有点的横坐标扩大到原来 2 倍（纵坐标不变）得函数 y=sinx 图象则 ω=____ φ=____ 。 解： y=sin2x =sin2(x- )=sin(2x- ) ω=2 φ=- 7 、 8 、 思路 : 函数 y=sin2x+acos2x 可化为 要使它的图象关于直线 x= -π/8 对称 , 则图象在该处必是处于波峰或波谷 . 即函数在 x=-π/8 时取得最大、小值 . 例 9 、 (98 年 ) 关于函数 有下列命题： ① 的表达式可改写为 ② 是以 为最小正周期的周期函数 ③ 的图象关于点 对称 ④ 的图象关于直线 对称 其中正确的命题序号是。 ① ③ （ 3 ）连线： 用“五点作图法”作出 y=A sin ( x +  ) 在长度为一个周期闭区间上的图象　　 (2) 描点： （ 1 ）列表： 0 - A 0 A 0 y 0 x +  x y ( ,0) ( ,A) ( ,0) ( ,- A) ( ,0) (1) 由最大值点（或最小值点）定 A (2) 由两个关键点（特殊点）定  和  总 结 给出函数 y=Asin( x+) (A>0 , >0) 的图象求其解析式的一般方法： 6 、已知下图是函数 的图象 (1) 求 的值； (2) 求函数图象的对称轴方程 . O x 2 1 –1 –2 y ⑴ （ 2 ）函数图象的对称轴方程为 即 设函数 （ 1 ）求 ； （ 2 ）求函数 的单调递增区间； （ 3 ）画出函数 在区间 [0 ， π] 上的图象 . 图象的一条对称轴是直线 解析 : （ 1 ） 图象的一条对称轴 , 是 O y x （ 2 ） 函数 的单调递增区间为 x y π o -1 1 x∈[0,π] （ 3 ） 5 ) 函数 (A>0, >0) 的一个周期内的图象如图，则有 ( ) (A) (B) (C) (D) y x 0 3 - 3 y x 0 2 -2 - 4 如图：根据函数 y= A sin ( x + ) (A>0 , >0) 图象求它的解析式 y x 0 -4 4 如图：根据函数 y = A sin ( x + ) (A>0 , >0) 图象 求它的解析式 y x 0 2 -2 如图：根据函数 y = A sin ( x + ) (A>0 , >0) 图象求它的解析式 y x 0 1 2 如图：根据函数 y = 2 sin( x + ) ( >0) 图象 求它的解析式 y x 0 1 2 如图：根据函数 y = 2 sin( x + ) ( >0) 图象 求它的解析式 y x 　　根据正弦函数的图象和性质寻找区间使其满足： 使符合条件的 的角 x 有且只有一个，而且包括锐角． 4.11 已知三角函数值求角 在闭区间 上，符合条件 的角 x ，叫做 实数 a 的反正弦，记作 ，即 ，其中 ， 且 ． 的意义： 首先 表示一个角，角的正弦值为 a ，即 ．角的范围是 4.11 已知三角函数值求角 练习： （ 1 ） 表示什么意思？ 表示 上正弦值等于 的那个角，即角 ， 故 （ 2 ）若 ，则 x = （ 3 ）若 ，则 x= 4.11 已知三角函数值求角 的意义： 首先 表示一个角，角的余弦值为 a ，即 ．角的范围是 ． 　　根据余弦函数的图象和性质寻找区间使其满足： 使符合条件的 的角 x 有且只有一个，而且包括锐角． y x 在闭区间 上，符合条件 的角 x ，叫做 实数 a 的反余弦，记作 ，即 ，其中 ， 且 ． 4 、已知三角函数值求角 y=sinx , 的反函数 y=arcsinx , y=cosx, 的反函数 y=arccosx, y=tanx, 的反函数 y=arctanx, ⑵ 已知角 x ( ) 的三角函数值求 x 的步骤 ① 先确定 x 是第几象限角 ② 若 x 的三角函数值为正的，求出对应的锐角 ；若 x 的三角函数 值为负的，求出与其绝对值对应的锐角 ③ 根据 x 是第几象限角，求出 x 若 x 为第二象限角，即得 x= ；若 x 为第三象限角，即得 x= ；若 x 为第四象限角，即得 x= ④ 若 ，则在上面的基础上加上相应函数的周期的整数倍。 ⑴ 反三角函数 已知三角函数值求角 已知三角函数值求角 x （仅限于 [0 ， 2 π] ）的解题步骤： 1 、如果函数值为正数，则求出对应的锐角 x 0 ；如果函数值为负数，则求出与其绝对值相对应的锐角 x 0 ； 2 、由函数值的符号决定角 x 可能的象限角； 3 、根据角 x 的可能的象限角得出 [0 ， 2 π] 内对应的角： 如果 x 是第二象限角，那么可以表示为 π － x 0 如果 x 是第三象限角，那么可以表示为 π ＋ x 0 如果 x 是第四象限角，那么可以表示为 2π － x 0 说明 : 三角函数值求角，关键在于角所属范围，这点不容忽视 . (1) 判断角的象限 ； (2) 求对应锐角； 如果函数值为正数，则先求出对应的锐角 x 1 ； 如果函数值为负数，则先求出与其绝对值对应的锐角 x 1 . (3) 求出 (0 ， 2 π ) 内对应的角 ； 如果它是第二象限角，那么可表示为－ x 1 ＋ π ； 如果它是第三或第四象限角，则可表示为 x 1 ＋ π 或－ x 1 ＋ 2 π . (4) 求出一般解 利用终边相同的角有相同的三角函数值这一规律 写出结果 . （三）已知三角函数值求角”的基本步骤 1 、基本步骤 2 、表示角的一种方法 —— 反三角函数法 1 、反正弦： 这时 sin(arcsin a)=a 2 、反余弦： 这时 cos(arccos a)=a 这时 tan(arctan a)=a 3 、反正切： 三、两角和与差的三角函数 1 、预备知识：两点间距离公式 x y o ● ● 2 、两角和与差的三角函数 注：公式的逆用 及变形的应用 公式变形 3 、倍角公式 一、知识点 （一） 两角和与差公式 （二）倍角 公式 ★ 公式 =1-cos 2 α 2cos2α=1+cos 2 α 1+cos2α=2cos 2 α 1-cos2α=2sin 2 α tanα+tanβ=tan(α+β)(1-tanαtanβ) tanα-tanβ=tan(α-β)(1+tanαtanβ) 注意 1 、公式的变形如： 注意 2 、公式成立的条件（使等式两边都有意义） . C α±β ： S α ± β ： C 2 α ： S 2α ： T 2 α ： T α ± β ： 倍角公式： 注：正弦与余弦的倍角公式的逆用实质上就是降幂的过程。特别 和角公式的一个重要变形 其 它 公 式 1 、半角公式 2 、万能公式 二、两角和与差的正弦、余弦、正切： 注意： 、 的 变形式 以及运用和差公式时要会 拼角 如： 要熟悉公式逆用！ 三、一个化同角同函数名的常用方法： 如： 例、求 的值 四、二倍角公式： 降幂（扩角）公式 升幂（缩角）公式 和差化积公式： 积化和差公式： 例 4 ．化简： 解法 1 ：从“角”入手，“复角”化为“单角”，利用“升幂公式”。 例 4 ．化简： 解法 2 ：从“幂”入手，利用“降幂公式”。 例 4 ．化简： 解法 3 ：从“名”入手，“异名化同名”。 例 4 ．化简： 解法 4 ：从“形”入手，利用“配方法”。 三角解题常规 宏观思路 分析差异 寻找联系 促进转化 指角的、函数的、运算的差异 利用有关公式，建立差异间关系 活用公式，差异转化，矛盾统一 微观直觉 1 、以变角为主线，注意配凑和转化； 2 、见切割，想化弦；个别情况弦化切； 3 、见和差，想化积；见乘积，化和差； 4 、见分式，想通分，使分母最简； 5 、见平方想降幂，见“ 1±cosα” 想升幂； 6 、见 sin2α ，想拆成 2sinαcosα ； 7 、见 sinα±cosα 或 9 、见 cosα·cosβ·cosθ···· ，先运用 sinα+sinβ=p cosα+cosβ=q 8 、见 a sinα+b cosα ，想化为 的形式 若不行，则化和差 10 、见 cosα+cos(α+β)+cos(α+2 β )… ， 想乘 想两边平方或和差化积 总结： 多种名称想切化弦；遇高次就降次消元； asinA+bcosA 提系数转换； 多角凑和差倍半可算； 难的问题隐含要显现； 任意变元可试特值算； 求值问题缩角是关键； 字母问题讨论想优先； 非特殊角问题想特角算； 周期问题化三个一再算； 适时联想联想是关键！ 【 解题回顾 】 找出非特殊角和特殊角之间的关系 , 这种技巧在化简求值中经常用到，并且三角式变形有规律即坚持“ 四化 ”： 多角同角化 异名同名化 切割弦化 特值特角互化 公式体系的推导： 首先利用两点间的距离公式推导 ， 然后利用换元及等价转化等思想方法，以 为中心推导公式体系。 sin ²α +cos ²α =1 二【述评】 1 、变为主线，抓好训练。变是本章的主题，在三角变换考查中，角的变换（恒等）、三角函数名的变换（诱导公式）、三角函数次数的变换（升、降幂公式）、三角函数表达式的变换（综合）等比比皆是。在训练中，强化变化意识是关键。但题目不可以太难。较特殊技巧的题目不做。立足课本，掌握课本中常见问题的解法，把课本中的习题进行归类，并进行分析比较，寻找解题规律。 2 、基本解题规律：观察差异（角或函数或运算） 寻找联系（借助于熟知的公式、方法或技巧） 分析综合（由因导果或执果索因） 实现转化。 1 、值域与最值问题 ① 利用有界性 ② 化二次函数型 ③ 运用合一变换 ④ 换元 十七、 求值域问题 ： 主要是将式子化成 同角度同函数名 的形式，再利用正弦 函数与余弦函数的 有界性 求解。 例 10 、求函数 的值域 有时还要运用到 的关系 2 、对称性问题 3 、奇偶性与周期性问题 注意绝对值的影响 化为单一三角函数 4 、单调性与单调区间 复后函数 单调性 注意负号 的处理 5 、图像变换问题 ① 相位变换、周期变换、振幅变换 ② 求函数解析式 例 5: 已知函数 求： ⑴ 函数的最小正周期； ⑵ 函数的单增区间； 解： ⑴ ⑵ 应用 ：化同一个角同一个函数 例 5: 已知函数 求： ⑶ 函数的最大值 及相应的 x 的值； ⑷ 函数的图象可以由函数 的图象经过怎 样的变换得到。 解： ⑶ ⑷ 图象向左平移 个单位 图象向上平移 2 个单位 应用 ：化同一个角同一个函数 例 6 ：已知 解： 应用： 化简求值 例 1 化简： 解 : ∵ ∴ 原式 = 练习题 例 2 (1) 已知 求证： (2) 已知 求 (1) 证明： ∴ ∴ 化简得： ∴ ∵ (2) 已知 求 解 : ∵ ∴ ∵ ∴ ∵ ∴ ∴ 解： 应用：化简求值 例 5. 已知 ∵ ∴ ∴ 2 、解 : 由 两边平方得 : ① 2 由 两边平方得 : ② 2 由 ① 2 +② 2 得 : 即 所以 由 ② 2 － ① 2 得 : 练习 已知 求 解 : ∵ ∴ ∵ ∴ ∴ ∴ 例 3. 已知函数 f ( x ) ＝ sin(2 x － ) ＋ 2sin 2 ( x － ) ( x ∈ R ) ． （ 1 ）求函数 f ( x ) 的最小正周期； （ 2 ）求使函数 f ( x ) 取最大值的 x 的集合． 解： f ( x ) ＝ sin(2 x － ) ＋ 1 － cos2( x － ) ＝ sin(2 x － ) － cos(2 x － ) ＋ 1 ＝ 2 sin(2 x － ) ＋ 1 ． 函数 f ( x ) 的最小正周期 T ＝  . 使函数 f ( x ) 取最大值的 x 的集合为 { x | x = k  ＋ ,k ∈ Z } ． 5 、已知 f(x)=2sin(x+ )cos(x+ )+2 cos 2 (x+ )- 。 （ 1 ）化简 f(x) 的解析式； （ 2 ）若 0 ≤ θ ≤ π ，求 θ ，使函数 f(x) 为偶函数。 （ 3 ）在（ 2 ）成立的条件下，求满足 f(x)=1 ， x ∈ [- π , π ] 的 x 的集合。 解： (1)f(x)=sin(2x+θ)+ [2cos 2 (x+ )-1] =sin(2x+θ)+ cos(2x+θ)=2cos(2x+θ- ) (2) 当 θ = 时 f(x) 为偶函数。 (3) 2cos2x=1 cos2x= x= ± 或 x= ± 例 6 、已知函数 f(x)=sin(x+ )+sin(x- )+cosx+a (a ∈ R,a 常数 ) 。 （ 1 ）求函数 f(x) 的最小正周期； （ 2 ）若 x ∈ [- , ] 时， f(x) 的最大值为 1 ，求 a 的值。 解：（ 1 ） f(x)=sin(x+ )+sin(x- )+cosx+a = sinx+cosx+a =2sin(x+ )+a ∴ f(x) 最小正周期 T=2 （ 2 ） x [- , ] ∴ x+ ∈ [- , ] ∴ f(x) 大 =2+a ∴ a=-1 例 7 、求函数 的值域 . 解： 又 ∵-1≤sinx≤1 ∴ 原函数的值域为： 变题： 已知函数 （ a 为常 数，且 a ＜ 0 ），求该函数的最小值 . 当 -2≤ ＜ 0 时， 当 ＜ -2 时， 1 、已知 a>0 函数 y=-acos2x- asin2x+2a+b x ∈ [0, ] ，若函数的值域为 [-5,1] ，求常数 a,b 的值。 解： 3a+b=1 ∴ a=2 b=-5 b=-5 2 、 函数 f(x)=1-2a-2acosx-2sin 2 x 的最小值为 g(a)(a ∈ R) ： （ 1 ）求 g(a) ； （ 2 ）若 g(a)= ，求 a 及此时 f(x) 的最大值 。 解：（ 1 ） f(x)=2(cosx- ) 2 - 2 -2a-1 -1 ≤ cosx ≤ 1 ① 当 -1 ≤ ≤ 1 即 -2 ≤ a ≤ 2 时 f(x) 小 =- 2 -a-1 ② 当 >1 即 a>2 时 f(x) 小 =f(1)=1-4a ③ 当 <-1 即 a<-2 时 f(x) 小 =f(-1)=1 （ 2 ） a=-1 此时 f(x)=2(cosx+ ) 2 + f(x) 大 =5 2 、 函数 f(x)=1-2a-2acosx-2sin 2 x 的最小值为 g(a)(a ∈ R) ： （ 1 ）求 g(a) ； （ 2 ）若 g(a)= ，求 a 及此时 f(x) 的最大值 。 3 、已知 f(x)=2sin(x+ )cos(x+ )+2 cos 2 (x+ )- 。 （ 1 ）化简 f(x) 的解析式； （ 2 ）若 0 ≤ θ ≤ π ，求 θ ，使函数 f(x) 为偶函数。 （ 3 ）在（ 2 ）成立的条件下，求满足 f(x)=1 ， x ∈ [- π , π ] 的 x 的集合。 解： (1)f(x)=sin(2x+θ)+ [2cos 2 (x+ )-1] =sin(2x+θ)+ cos(2x+θ)=2cos(2x+θ- ) (2) 当 θ = 时 f(x) 为偶函数。 (3) 2cos2x=1 cos2x= x= ± 或 x= ± 例 4. 已知函数 f ( x ) ＝ a sin x － b cos x （ a ， b 为常数， a ≠0 ， x ∈ R ） 在 x ＝ 处取得最小值， 则函数 y ＝ f ( － x ) 的对称中心坐标是 ____________ ． 解：由 ( a － b ) ＝－ 化简得 a ＝－ b ． 所以 f ( x ) ＝ a sin( x ＋ ) ， a ＜ 0 ． 从而 f ( － x ) ＝ a sin x ， 其对称中心坐标为 ( k  ， 0) ， k ∈ Z . 平 面 向 量 复 习 向量的三种表示 表示 运算 向量加 法与减法 向量的相关概念 实数与 向量 的积 三 角 形 法 则 平行四边形法则 向量平行、 垂直的条件 平面向量 的基本定理 平 面 向 量 向量的数量积 向量的应用 几何表示 : 有向线段 向量的表示 字母表示 坐标表示 : ( x ， y ) 若 A(x 1 ,y 1 ), B(x 2 ,y 2 ) 则 AB = (x 2 － x 1 , y 2 － y 1 ) 返回 1. 向量的概念 : 2. 向量的表示 : 3. 零向量 : 4. 单位向量 : 5. 平行向量 : 6. 相等向量 : 7. 共线向量 : 既有大小又有方向的量 1. 有向线段 2. 字母 3. 有向线段起点和终点字母 长度为零的向量 ( 零向量与任意向量都平行 长度为 1 个单位的向量 1. 方向相同或相反的非零向量 2. 零向量与任一向量平行 长度相等且方向相同的向量 平行向量就是共线向量 向量的模（长度） 1. 设 a = ( x , y ), 则 2. 若表示向量 a 的起点和终点的坐标分别 为 A (x 1 ,y 1 ) 、 B (x 2 ,y 2 ) ，则 返回 例 1 ：思考下列问题 ： 1 、下列命题正确的是 （ 1 ）共线向量都相等 （ 2 ）单位向量都相等 （ 3 ）平行向量不一定是共线向量 （ 4 ）零向量与任一向量平行 四、例题 一、第一层次 知识回顾 ： 1. 向量的加法运算 O A B 三角形法则 O A B C 平行四边形法则 坐标运算 设： 则 “ 首尾相接首尾连” 2. 向量的减法运算 1 ） 减法法则 ： O A B 2 ） 坐标运算 设： 则 设 则 思考： 若 非零向量 ， 则它们的模相等且方向相同。 同样 若： “ 同始点尾尾相接 , 指向被减向量” 一、第一层次 知识回顾 ： 1. 向量的加法运算 A B C AB+BC= 三角形法则 O A B C OA+OB= 平行四边形法则 坐标运算 : 则 a + b = 重要结论： AB+BC+CA= 0 设 a = (x 1 , y 1 ), b = (x 2 , y 2 ) ( x 1 + x 2 , y 1 + y 2 ) AC OC 例题： 实数 λ 与向量 a 的积 定义 ： 坐标运算： 其实质就是向量的伸长或缩短！ λ a 是一个 向量 . 它的 长度 | λ a | = | λ | | a | ； 它的 方向 (1) 当 λ≥0 时 , λ a 的方向 与 a 方向 相同 ； (2) 当 λ ＜ 0 时 , λ a 的方向 与 a 方向 相反 . 若 a = (x , y), 则 λ a = λ (x , y) = ( λ x , λ y) 返回 平面向量的数量积 （ 1 ） a 与 b 的夹角 ： （ 2 ）向量夹角的范围 ： （ 3 ）向量垂直 ： [0 0 ， 180 0 ] a b θ 共同的起点 a O A B b θ O A B O A B O A B O A B （ 4 ）两个非零向量的数量积： 规定： 零向量与任一向量的数量积为 0 a · b = |a| |b| cosθ 几何意义： 数量积 a ·b 等于 a 的长度 |a| 与 b 在 a 的方向上的投影 |b| cosθ 的乘积 。 A a b θ B B 1 O B A θ b B 1 a O θ B b (B 1 ) A a O 若 a=( x 1 , y 1 ), b=( x 2 , y 2 ) 则 a · b= x 1 · x 2 + y 1 · y 2 5 、数量积的运算律： ⑴ 交换律： ⑵ 对数乘的结合律： ⑶ 分配律： 注意： 数量积不满足结合律 返回 3. 平面向量的数量积的性质 (1) a ⊥ b  a·b ＝ 0 (2) a·b ＝ ± |a|·|b|(a 与 b 同向取正，反向取负 ) (3) a·a ＝ |a| 2 或 |a| ＝ √ a·a (4) (5) |a·b|≤|a||b| 4. 平面向量的数量积的坐标表示 (1) 设 a ＝ (x 1 ， y 1 ) ， b ＝ (x 2 ， y 2 ) ， 则 a·b ＝ x 1 x 2 +y 1 y 2 ， |a| 2 ＝ x 2 1 +y 2 1 ， |a| ＝ √ x 2 1 +y 2 1 ， a ⊥ b <=> x 1 x 2 +y 1 y 2 ＝ 0 (2) (3) 设 a 起点 (x 1 ， y 1 ), 终点 (x 2 ， y 2 ) 则 5 、重要定理和公式： 　 　　 ⑵ ⑶ 设 则 ⑷ 设两点 则 ⑸ 设 则 ⑴ 设非零向量 则　 二、平面向量之间关系 向量平行 ( 共线 ) 条件的两种形式 : 向量垂直条件的两种形式 : （ 3 ）两个向量相等的条件是两个向量的 坐标相等 . 即 : 那么 3 、平面向量的坐标运算 — 知识回忆 （ 1 ） e 1 、 e 2 不共线， a=λ 1 e 1 +λ 2 e 2 ( 存在一对实数 λ 1 ， λ 2 ) ( λ 1 ， λ 2 唯一的 ) 。 （ 2 ） a=xi+yj (x,y) 为 a 的直角坐标， a= (x,y) （ 3 ） ① 若 a=(x 1 ,y 1 ) b=(x 2 ,y 2 ) ， 则 a±b= (x 1 ± x 2 ,y 1 ± y 2 ) ② A (x 1 ,y 1 ) B( x 2 ,y 2 ) AB= (x 2 -x 1 ,y 2 -y 1 ) ③ 若 a= (x,y) 则 λa=( λx,λy ) ④ a= (x 1 ,y 1 ) b= (x 2 ,y 2 ) (b ≠ 0) a ∥ b x 1 y 2 -x 2 y 1 =0 知识回忆 典例分析 例 5 例 6 回目录 例题 解这个方程组得 k =-(1/3), λ =-(1/3), 即当 k =-(1/3) 时， k a+b 与 a-3b 平行，这时 k a+b=-a/3+b. 因为 λ =-(1/3)<0, 所以 -a/3+b 与 a-3b 反向。 在本例中，也可以根据向量平行充分条件的坐标 形式，从 (k-3)  (-4)-10  (2k+2)=0, 先解出 k=-(1/3) ，然后再求 λ 。 注 例 2 设 a ， b 是两个不共线向量。 AB=2a+kb BC=a+b CD=a-2b A 、 B 、 D 共线则 k=_____(k ∈ R) 解： BD=BC+CD=a+b+a-2b=2a-b 2a+kb=λ(2a-b)=2λa-λb 2=2λ λ=-1 k=-λ k=-1 ∴ k=-1 ∴ 知识回忆 典例分析 例 2 例 3 例 4 2 、实数与向量的积 — 典例分析 - 例 2 本页结束 回目录 1 ．与平面几何的结合： A B D C A B D C 四边形 ABCD 是菱形 四边形 ABCD 是矩形 A B C O A B C D M A B C O M 外心 重心 重心 第一层次 例题分析 类型四：三角形中的向量问题 重要结论： A B C O 第一层次 例题分析 类型四：三角形中的向量问题 练习 1 ：判断正误，并简述理由。 ( √ ） ( √ ） ( √ ） ( × ） ( × ） ( × ） 平 面 向 量 复 习 2. 设 AB=2( a +5 b ) ， BC=  2 a + 8 b ， CD=3( a  b ) ， 求证： A 、 B 、 D 三点共线。 分析 要证 A 、 B 、 D 三点共线，可证 AB=λBD 关键是找到 λ 解： ∵BD=BC+CD=  2 a + 8 b+ 3( a  b )= a+5b ∴AB=2 BD 且 AB 与 BD 有公共点 B ∴ A 、 B 、 D 三点共线 AB∥ B D