- 2021-04-16 发布 |
- 37.5 KB |
- 18页


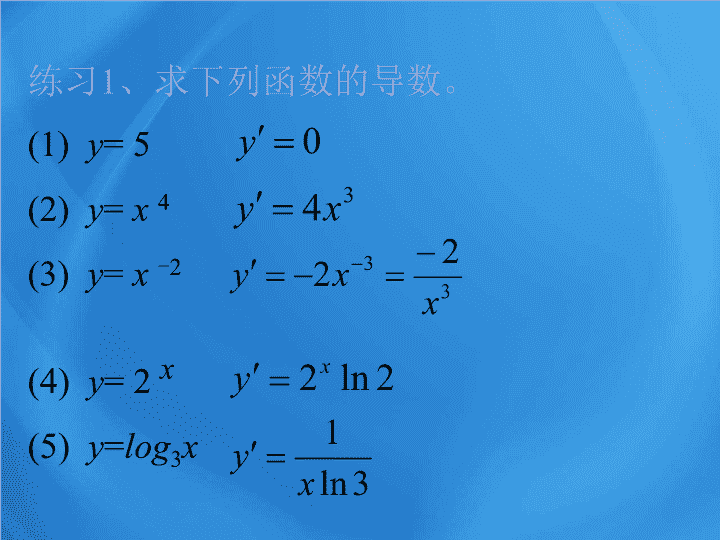
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版高中数学选修1-1课件:4_导数的运算法则
3.2.2 基本初等函数的导数公式及导数的运算法则 我们今后可以直接使用的基本初等函数的导数公式 练习 1 、求下列函数的导数。 (1) y = 5 (2) y = x 4 (3) y = x - 2 y = 2 x y = log 3 x 思考如何求下列函数的导数: 解 : 根据 基本初等函数导数公式表 , 有 所以 因此 , 在第 10 个年头 , 这种商品的价格 约以 0.08 元 / 年的速度上涨 . 导数的运算法则 : 法则 1: 两个函数的和 ( 差 ) 的导数 , 等于这两个函数的导数的 和 ( 差 ), 即 : 法则 2: 两个函数的积的导数 , 等于第一个函数的导数乘第二个函数 , 加上第一个函数乘第二个函数的导数 , 即 : 法则 3: 两个函数的商的导数 , 等于第一个函数的导数乘第二个函数 , 减去第一个函数乘第二个函数的导数 , 再除以第二个函数的平方 . 即 : 如果上式中 f ( x )= c, 则公式变为: 例 2 根据基本初等函数的导数公式和导数 运算法则,求函数 y = x 3 -2 x +3 的导数。 解:因为 所以,函数 y = x 3 -2 x +3 的导数是 练习 2 、求下列函数的导数。 解:净化费用的瞬时变化率就是净化费用 函数的导数。 因为 ,所以, 纯净度为 90% 时,费用的瞬时变化率 为 52.84 元 / 吨。 (2) 因为 ,所以, 纯净度为 98% 时,费用的瞬时变化率 为 1321 元 / 吨。 例 4: 求下列函数的导数 : 答案 : 例 5. 某运动物体自始点起经过 t 秒后的距离 s 满足 s= -4t 3 +16t 2 . (1) 此物体什么时刻在始点 ? (2) 什么时刻它的速度为零 ? 解 :(1) 令 s=0, 即 1/4t 4 -4t 3 +16t 2 =0, 所以 t 2 (t-8) 2 =0, 解得 : t 1 =0,t 2 =8. 故在 t=0 或 t=8 秒末的时刻运动物体在 始点 . 即 t 3 -12t 2 +32t=0, 解得 :t 1 =0,t 2 =4,t 3 =8, 故在 t=0,t=4 和 t=8 秒时物体运动的速度为零 . 我们再回顾一下 “ 导数的几何意义 ” 中的两个练习题。 练习 1 、求曲线 在点 M(3,3) 处的 切线的斜率及倾斜角. 斜率为 - 1, 倾斜角为 135° 第二种解法: 代入 x =3, 得 练习 2 、判断曲线 在( 1 , - )处 是否有切线,如果有, 求出切线的方程 . 1 2 有 , 切线的方程为 试自己动手解答 .查看更多