- 2021-04-16 发布 |
- 37.5 KB |
- 6页


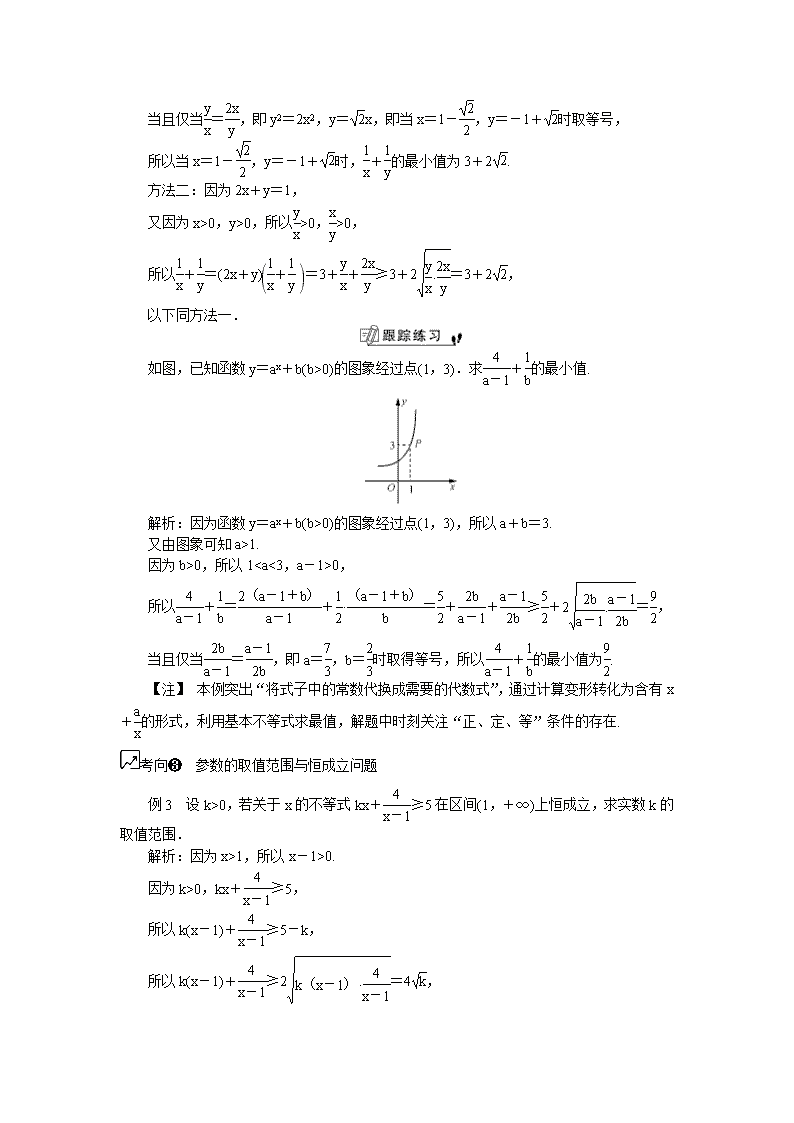
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习人教A版第37课基本不等式及其简单应用(1)学案(江苏专用)
____第37课__基本不等式及其简单应用(1)____ 1. 掌握两个正数的算术平均数不小于它的几何平均数定理,了解其证明过程. 2. 能熟练地应用基本不等式解决简单的最大(小)值问题. 1. 阅读:必修5第96~98页. 2. 解悟:①什么是教材规定的基本不等式?需要怎样的使用条件?证明其正确性有哪几种证法?②基本不等式有几个常用的变形形式及其使用的条件?③“和定积最大”“积定和最小”是怎样得到的?请用符号语言表示出来;④教材必修5第98页关于基本不等式的几何解释,你能理解吗? 3. 践习:在教材空白处,完成必修5第98~99页练习第2、3、4、5题. 基础诊断 1. 已知mn=8(m>0,n>0),则m+n的最小值为__4__. 解析:因为m>0,n>0,所以m+n≥2=4,当且仅当m=n=2时,等号成立. 2. 下列命题正确的是__②__.(填序号) ①函数y=x+的最小值是2; ②函数y=sinx+,x∈的最小值是2; ③函数y=的最小值是2; ④函数y=2-3x-的最大值是2-4. 解析:对于①,当x>0时,y=x+≥2,当且仅当x=1时取等号,当x=0时,y=x+无意义,当x<0时,y=x+=-≤-2,当且仅当x=y=-1时取等号,故y=x+的值域为(-∞,-2]∪[2,+∞),无最小值;对于②,因为x∈,所以sinx∈(0,1],y=sinx+≥2,当且仅当sinx=1,即x=时取等号,故②正确;对于③,y==+,令t=,则y=t+,t∈[2,+∞).因为y=t+在[2,+∞)上为增函数,所以ymin=2+=,故③错误;对于④,当x>0时,y=2-3x-≤2-2=2-4,当且仅当x=时取等号.当x<0时,y=2-3x-≥2+4.当且仅当x=-时取等号,故④错误. 3. 已知x<,则函数f(x)=4x-2+的最大值为__1__. 解析:因为x<,所以4x-5<0,所以y=4x-2+=4x-5++3=3-(5-4x+)≤3-2=1,当且仅当x=1时取等号,所以f(x)=4x-2+的最大值为1. 4. 设a>0,b>0,且a+b=1,则+的最小值为__4__. 解析:因为a+b=1,所以+=(a+b)·=1+++1=2++≥2+2=4,当且仅当=,即a=b=时,取等号. 范例导航 考向❶ 通过简单构造和变形,运用基本不等式求最值 例1 求函数f(x)=x+(x>2)的最小值. 解析:因为x>2,所以x-2>0, 所以f(x)=x-2++2≥2+2=4,当且仅当x-2=,即x=3∈(2,+∞)时取等号.所以当x=3时,函数f(x)min=4. 当x>0时,求函数f(x)=的最大值. 解析:因为x>0,所以f(x)===≤=1,当且仅当x=,即x=1∈(0,+∞)时,取等号,所以当x=1时,函数f(x)max=1. 【注】 本例突出构造x+型,利用基本不等式求最值,解题中时刻关注“正、定、等”条件的存在. 考向❷ 通过常值代换,运用基本不等式求最值 例2 已知x>0,y>0,且2x+y=1,求+的最小值. 解析:方法一:因为2x+y=1, 又因为x>0,y>0,所以>0,>0, 所以+=+=3++≥3+2=3+2, 当且仅当=,即y2=2x2,y=x,即当x=1-,y=-1+时取等号, 所以当x=1-,y=-1+时,+的最小值为3+2. 方法二:因为2x+y=1, 又因为x>0,y>0,所以>0,>0, 所以+=(2x+y)=3++≥3+2=3+2, 以下同方法一. 如图,已知函数y=ax+b(b>0)的图象经过点(1,3).求+的最小值. 解析:因为函数y=ax+b(b>0)的图象经过点(1,3),所以a+b=3. 又由图象可知a>1. 因为b>0,所以1查看更多