2019届高三数学(文)二轮复习查漏补缺课时练习:(十四) 第14讲 导数与函数的单调性
课时作业(十四) 第14讲 导数与函数的单调性
时间 / 45分钟 分值 / 100分
基础热身
1.函数y=x(x2-6)的单调递减区间是 ( )
A.(-∞,2)
B.(2,+∞)
C.(-2,2)
D.(0,2)
2.函数f(x)=1+x-cos x在(0,2π)上的单调情况是 ( )
A.单调递增
B.单调递减
C.在(0,π)上单调递增,在(π,2π)上单调递减
D.在(0,π)上单调递减,在(π,2π)上单调递增
3.函数y=(x+1)ex的单调递增区间是 ( )
A.(-∞,1]
B.(-∞,-2]
C.[1,+∞)
D.[-2,+∞)
4.函数f(x)=ln x-2ax(a>0)的单调递增区间是(0,2),则实数a= ( )
A.12 B.13
C.14 D.1
5.函数f(x)=ln x-12x2+x的单调递增区间为 .
能力提升
6.若f(x)=x3-ax2+1在(1,3)上单调递减,则实数a的取值范围是 ( )
A.(-∞,3]
B.92,+∞
C.3,92
D.(0,3)
7.已知函数f(x)=sin x-x,则不等式f(x+1)+f(2-2x)>0的解集是 ( )
A.-∞,-13
B.-13,+∞
C.(3,+∞)
D.(-∞,3)
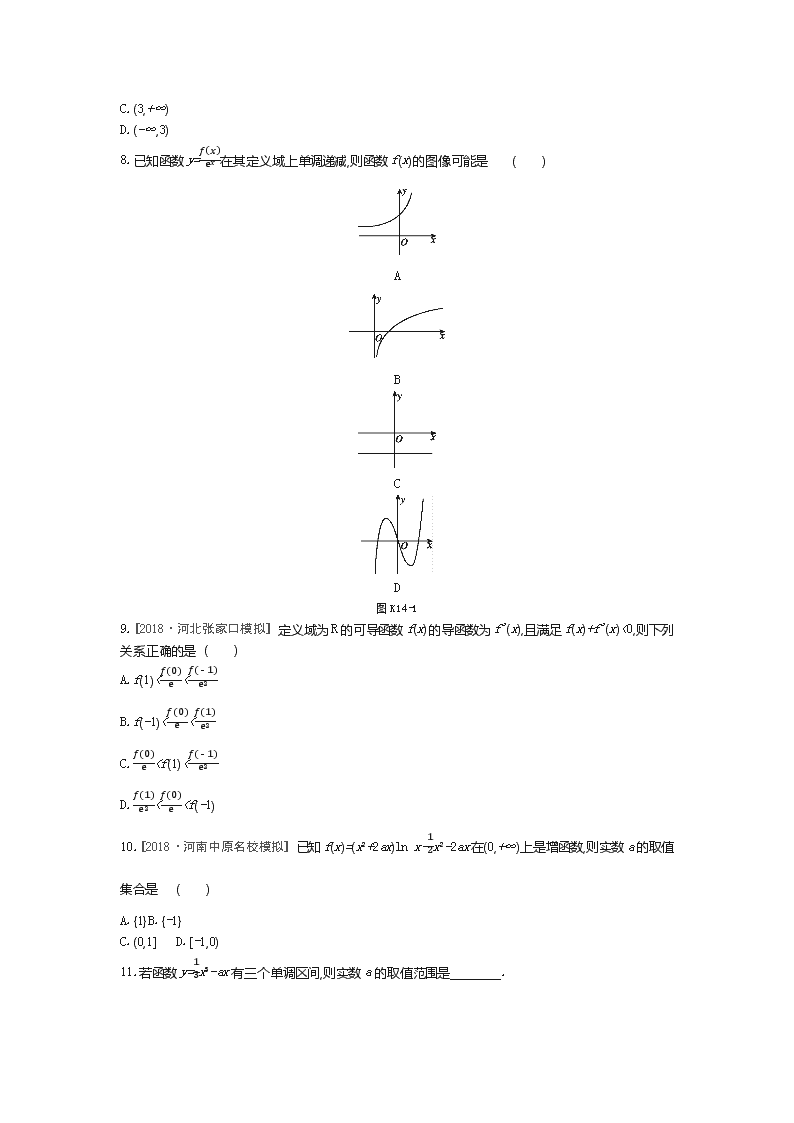
8.已知函数y=f(x)ex在其定义域上单调递减,则函数f(x)的图像可能是 ( )
A
B
C
D
图K14-1
9.[2018·河北张家口模拟] 定义域为R的可导函数f(x)的导函数为f'(x),且满足f(x)+f'(x)<0,则下列关系正确的是 ( )
A.f(1)
-x0·f'(x0)成立,则实数b的取值范围是 .
14.(12分)已知函数f(x)=x3+ax2+2x-1.
(1)若函数f(x)在区间[1,3]上单调递增,求实数a的取值范围;
(2)若函数f(x)在区间[-2,-1]上单调递减,求实数a的取值范围.
15.(13分)设函数f(x)=eax+λln x,其中a<0,e是自然对数的底数.若f(x)是(0,+∞)上的单调函数,求λ的取值范围.
难点突破
16.(5分)[2018·昆明三模] 已知函数f(x)=(x2-2x)ex-aln x(a∈R)在区间(0,+∞)上单调递增,则a的最大值是 ( )
A.-e B.e
C.-e22 D.4e2
17.(5分)已知函数f(x)=x-2(ex-e-x),则不等式f(x2-2x)>0的解集为 .
课时作业(十四)
1.C [解析] y=x(x2-6)=x3-6x,则y'=3x2-6,由y'<0得-20,所以由y'≥0得x+2≥0,得x≥-2,故选D.
4.C [解析] 由f(x)=ln x-2ax(a>0),得f'(x)=1x-2a,因为x>0,所以由f'(x)>0得00),由f'(x)>0,得0f(2x-2),由函数的单调性可知x+1<2x-2,得x>3.故选C.
8.A [解析] 因为函数y=f(x)ex在其定义域上单调递减,所以y'=f(x)ex'=f'(x)-f(x)ex≤0在定义域上恒成立且不恒为0,即f(x)≥f'(x)恒成立,结合函数f(x)的图像及导数的几何意义可得选项A满足条件.故选A.
9.A [解析] 设g(x)=exf(x),则g'(x)=ex[f(x)+f'(x)]<0,所以g(x)为R上的减函数,则g(-1)>g(0)>g(1),即e-1f(-1)>e0f(0)>e1f(1),整理得f(1)1时,ln x>0,要使f'(x)≥0恒成立,则x+a≥0恒成立,因为x+a>1+a,所以1+a≥0,解得a≥-1;当00 [解析] y'=x2-a,因为y=13x3-ax有三个单调区间,所以方程x2-a=0有两个不等实根,故a>0.
12.c0,f(x)单调递增,又f(3)=f(-1),且-1<0<12<1,所以f(-1)-x·f'(x),得f(x)+x·f'(x)>0,即[xf(x)]'>0,所以由题知1x+2(x-b)>0在12,2上有解,即b<12x+x在12,2上有解,当x∈12,2时,12x+x的最大值为14+2=94,所以b的取值范围是-∞,94.
14.解:由f(x)=x3+ax2+2x-1,得f'(x)=3x2+2ax+2.
(1)因为函数f(x)在区间[1,3]上单调递增,所以f'(x)≥0在[1,3]上恒成立,
即a≥-3x2-22x在[1,3]上恒成立.
令g(x)=-3x2-22x,则g'(x)=-3x2+22x2,
当x∈[1,3]时,g'(x)<0,所以g(x)在[1,3]上单调递减,所以g(x)max=g(1)=-52,所以a≥-52.
(2)因为函数f(x)在区间[-2,-1]上单调递减,所以f'(x)≤0在[-2,-1]上恒成立,即a≥-3x2-22x在[-2,-1]上恒成立,由(1)易知,g(x)=-3x2-22x在[-2,-1]上单调递减,所以a≥g(-2),即a≥72.
15.解:f'(x)=aeax+λx=axeax+λx(x>0).
①若λ≤0,则f'(x)<0,则f(x)是(0,+∞)上的减函数,满足题意.
②若λ>0,令g(x)=axeax+λ,其中a<0,x>0,则g'(x)=aeax(1+ax),令g'(x)=0,得x=-1a,
当x∈0,-1a时,g'(x)<0,g(x)单调递减,当x∈-1a,+∞时,g'(x)>0,g(x)单调递增.
故当x=-1a时,g(x)取得极小值,也是最小值,且g-1a=λ-1e.
因此当λ-1e≥0,即λ≥1e时,g(x)≥0,此时f'(x)≥0,f(x)是(0,+∞)上的增函数,满足题意.
综上所述,λ的取值范围是(-∞,0]∪1e,+∞.
16.A [解析] 因为函数f(x)=(x2-2x)ex-aln x(a∈R),所以f'(x)=ex(x2-2x)+ex(2x-2)-ax=ex(x2-2)-ax.因为函数f(x)=(x2-2x)ex-aln x(a∈R)在区间(0,+∞)上单调递增,所以f'(x)=ex(x2-2)-ax≥0在区间(0,+∞)上恒成立,即a≤ex(x3-2x)在区间(0,+∞)上恒成立.令h(x)=ex(x3-2x)(x>0),则h'(x)=ex(x3-2x)+ex(3x2-2)=ex(x3-2x+3x2-2)=ex(x-1)(x2+4x+2).令h'(x)>0,可得x>1,所以函数h(x)在区间(1,+∞)上单调递增,在区间(0,1)上单调递减,所以h(x)min=h(1)=-e,所以a≤-e.故选A.
17.(0,2) [解析] 由函数的解析式可得f'(x)=1-2(ex+e-x),由于ex+e-x≥2ex·e-x=2,当且仅当ex=e-x,即x=0时等号成立,所以f'(x)=1-2(ex+e-x)≤-3,则函数f(x)是R上的减函数.注意到f(0)=0,则题中的不等式等价于f(x2-2x)>f(0),结合函数的单调性有x2-2x<0,解得0
查看更多