数学文卷·2018届重庆市巴蜀中学高三适应性月考(七)(2018
巴蜀中学 2018 届高三适应性月考(七)
文科数学
一、选择题:本大题共 12 个小题,每小题 5 分,共 60 分.
1 已知 A={a,1,2},B={3,-1},A B={3},则 a=( ) A.1 B.2 C.3 D -1
2 已知复数 z=i+2i +i , 则|z|=( ) A. B C D 2
3 已知实数 x,y 满足 ,则 2x+y 的最大值为( )A.3 B.0 C.-1 D 2
4"|x|>0"是"x-1 e "的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
5 已知 x [-2,4].则 x 0 的概率为( ) A B C D
6 某几何体的三视图如图所示,则该几何体的体积为( )
A B C D
7 下列说法正确的是( )A 若 <1,则 a>1 B 若 y=x+ ,则 y 的最小值为 2
C y=3sin(x+1)是周期函数 D 平面非零的向量 , , 满足 = ,则 =
8 执行如图所示的程序框图,则输出的 n 的值为( ) A. 5 B. 7 C. 9 D 6
9 在 中,AB=AC=1,BC= ,D 为 BC 的中点,则 =( )A B C
D
10 已知函数 (x R)是单调递增的奇函数,等差数列{a }满足 f(a )+f(a )=0,则数
列{a }的前 11 项和为( )A.1 B.-1 C. 2 D 0
∩
2 10 2 5 10
≤
−≥
≥
1
y
y
xy
x
≥ 2
∈ ≥
3
2
7
4
5
2
3
1
22
3 +π 23 +π 42
3 +π 43 +π
a
1
x
1
a b c a b a c b c
ABC∆
2
1 ACAD•
16
15
4
1
4
15
16
15
)(xf ∈ n 3 9
n
11.已知双曲线 ,直线l的斜率为-2,与双曲线交于A,B,若在双曲线上存在异
于A,B的一点C,使直线AB,BC,AC的斜率满足 =3,若D,E,H三点
为AB,BC,AC的中点,则k +k =( ) A.-6 B.5 C.6 D.7
12 已知 f(x)= sin(x+ )cos(x+ )+cos (x+ )- (| |< ),若 f(0)= ,a=f( ),b=f( ),
c=f( ),则( )A a
= ppy
∈ ∞ 3 x
n 1 n n 1n+ ∈ ∗
n2
n
10na a− ∈ ∗
1 2 n 1 2 n-19
18 为了全面贯彻党的教育方针,坚持以人文本、德育为先,全面推进素质教育,让学生接
触自然,了解社会,拓宽视野,丰富知识,提高社会实践能力和综合素质,减轻学生过重负
担,培养学生兴趣爱好,丰富学生的课余生活,使广大学生在社会实践中,提高创新精神和
实践能力,树立学生社会责任感,因此学校鼓励学生利用课余时间参加社会活动实践。寒假
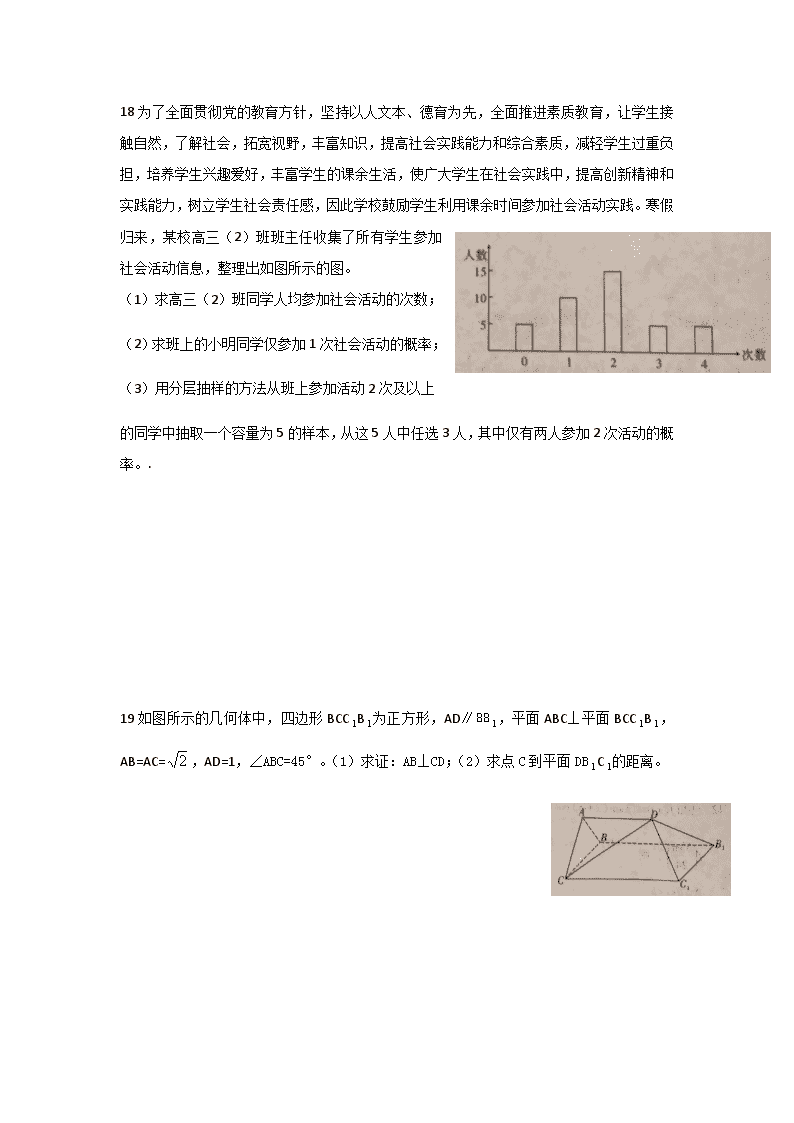
归来,某校高三(2)班班主任收集了所有学生参加
社会活动信息,整理出如图所示的图。
(1)求高三(2)班同学人均参加社会活动的次数;
(2)求班上的小明同学仅参加 1 次社会活动的概率;
(3)用分层抽样的方法从班上参加活动 2 次及以上
的同学中抽取一个容量为 5 的样本,从这 5 人中任选 3 人,其中仅有两人参加 2 次活动的概
率。.
19 如图所示的几何体中,四边形 BCC B 为正方形,AD∥BB ,平面 ABC⊥平面 BCC B ,
AB=AC= ,AD=1,∠ABC=45°。(1)求证:AB⊥CD;(2)求点 C 到平面 DB C 的距离。
1 1 1 1 1
2 1 1
20 已知椭圆 与直线 y= x-2 相切,设椭圆的上顶点为 M,
是椭圆的左右焦点,且⊿M 为等腰直角三角形。(1)求椭圆的标准方程;(2)直
线 l 过点 N(0,- )交椭圆于 A,B 两点,直线 MA、MB 分别与椭圆的短轴为直径的圆交于
S,T 两点,求证:O、S、T 三点共线。
21 已 知 函 数 f(x)=ln(x+1)-mx(m R) 。 (1) 若 m>0, 讨 论 f(x) 的 单 调 性 ; ( 2 ) 令
g(x)=f(x-1)+(2m+1)x+n,若 g(x)有两个零点 x ,x ,求证:x x <
22 选 修 4—4 : 在 直 角 坐 标 坐 标 系 中 , 过 点 P ( 1,0 ) 的 直 线 l 的 参 数 方 程 为
( 为参数, ),以坐标原点 为极点, 轴的正半轴为极轴建立
)0(12
2
2
2
>>=+ bab
y
a
x
2
2 2
21, FF 21FF
3
2
∈
1 2 1 2 2)1m
1
+(
xOy
=
+=
α
α
sin
cos1
ty
tx t ),(
20
πα ∈ O x
极坐标系,已知顶点在极轴上,开口向右的抛物线 C 经过极坐标为(2, )的点 Q。(1)
求 C 的极坐标方程;(2)若 l 与 C 交于 A、B 两点,且|PA|=2|PB|,求 tan 的值。
CCABA ACBDD DB 4, 2, , ,17① ②=;18
(Ⅰ) (Ⅱ) .(Ⅲ) 19 20 22① ②
23.选修 4-5:设 .(1)当 a=2 时,求不等式 的解集;
(2)若 a>0,b>0,c>0 且 ab+bc+ac=1,求证:当 x R 时,f(x)
巴蜀中学 2018 届高考适应性月考卷(七)文科数学参考答案
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C C A B A A C B D D D,] B 科]
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分)
题号 13 14 15 16
答案 4 2
三、解答题(共 70 分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分 12 分)解:(Ⅰ)取 , ,则 ,所以 ,
3
π
α
3 2 2+ 2 2(8e 4) 12e 4y x= − − + 2
( 1) (2 1).2n n
n nS S n n
+= = +,
10 30 15 20 15.40 8x
+ + += = 1
4P = 6 3.10 5
=
2.DO =
2 2
1.8 4
x y+ = 2sin 3cos .ρ θ θ=
6
|1|-||)( 2 +−= xaxxf 1)( ≤xf
∈ 222 2b ac ++≤
3 2 2+ 2 2(8e 4) 12e 4y x= − − +
1n = 1 1 22S a a= 2 2a = 2 1 1d a a= − =
所以 , ………………………………(6 分)
(Ⅱ)因为 ,所以 ,
,所以 …(12 分)
18.(本小题满分 12 分)解:(Ⅰ) ………………(4 分)
(Ⅱ)参加 1 次的有 10 人,班上有 40 人,则概率为 . …………………(7 分)
(Ⅲ)参加 2 次活动的抽 3 人,参加 3 次和 4 次活动的各 1 人,从这 5 人中任选 3 人有 10
种选法,其中仅有两人参加 2 次活动的有 6 种,则概率为 …(12 分)
19.(满分 12 分)(Ⅰ)证明:在三角形 ABC 中, , ,则
,
由 , 得 , 所 以 , 有
,
所以 ,所以 (6 分)
(Ⅱ)解:如图,取 BC 的中点 O, 的中点 M,连接 DO,DM,OM,
在三角形 DOM 中, ,所以 ,则 ,又
在三角形 中, ,所以 ,又 ,所以 ,
所以 ,所以 ,由 ,所以点 C 到平面 的距离
为 ……(12 分)
20.(本小题满分 12 分)(Ⅰ)解:由 为等腰直角三角形,则 则椭圆的方
程为 ,
又椭圆与直线相切,所以
, 相 切 , 则 , 所 以 椭 圆 的 标 准 方 程 为
…(5 分)
na n= 2
( 1) (2 1).2n n
n nS S n n
+= = +,
102 na a
nb −= 102n
nb −= 2 19
( 9) ( 8) 10 2
1 2 2 2 .
n n
n
nb b b
−
− + − + + −⋅⋅⋅ = =
( )
( 19)
( 9) ( 8) (9 ) 2
1 2 19 2 2
n n
n
nb b b
−
− + − + + −
−⋅⋅⋅ = = 1 2 1 2 19 .n nb b b b b b −⋅⋅⋅ =
10 30 15 20 15.40 8x
+ + += =
1
4P =
6 3.10 5
=
2AB AC= = 45ABC∠ = °
AB AC⊥
1 1ABC BCC B⊥平面 平面 1CC BC⊥ 1CC ABC⊥ 平面
1CC AB⊥
AB ACD⊥ 平面 .AB CD⊥
1 1B C
2 2DO DM OM= = =, 2 2 2DO DM MO+ = DO DM⊥
1 1DB C 1 1DB DC= 1 1DM B C⊥ 1 1OM B C⊥ 1 1B C DOM⊥ 平面
1 1DO B C⊥ 1 1DO DB C⊥ 平面 1 1BC DB C∥平面 1 1DB C
2.DO =
1 2MF F△
2
b c
a b
= =
,
,
2 2 22 2x y b+ =
2 2 2
2 2 2 22 2 ( 2 4) 2 2 4 8 2 16
2 4
x y b y y b y y
x y
+ = ⇒ + + = ⇒ + + = +
,
22 0b− = 2 2128 16(16 2 ) 0 4b b∆ = − − = ⇒ =
2 2
1.8 4
x y+ =
( Ⅱ ) 证 明 : 设 点 , 设 直 线 AB 的 斜 率 为 k , 则 直 线 为
,
联立 消去 y 得 ,所以
又 ,所以 ,
所以 ,带入韦达定理有:
,
所以 ,所以在圆中, ,所以点 三点共线. ………(12 分)
21 .( 本 小 题 满 分 12 分 ) 解 : ( Ⅰ ) 因 为 , 令
,
所以 的单调增区间为 ,单调递减区间为 …………(4 分)
(Ⅱ)由题意得 ,有
两式相减得 ,…(5 分)
要证 ,即证 , …(7
分)
不妨设 ,则 ,则只需证 .令 ,
则 … ( 9 分 ) 令 , 则
,所以 在 上单调递减,所以 ,所以 在
上单调递增,所以 ,即 在 上恒成立,原不等式成
立.…(12 分)
1 1 2 2( ) ( )A x y B x y, , , AB
2
3y kx= −
2 2
2
3
2 8
y kx
x y
= −
+ =
,
,
2 2 8 64(1 2 ) 03 9k x kx+ − − = 1 2 2
1 2 2
8
3
1 2
64
9
1 2
k
x x k
x x k
+ = +
− = +
,
,
(0 2)M , 1 2 1 2 1 2 1 2
8 8( 2)( 2) 3 3MA MB x x y y x x kx kx = + − − = + − −
2
1 2 1 2
8 64(1 ) ( )3 9MA MB k x x k x x= + − + +
2 2 2 2
2 2 2
64 1 64 64 64 1 1 09 1 2 9 1 2 9 9 1 2
k k k kMA MB k k k
+ + += − − + = − + = + + +
MA MB⊥ π
2SMT∠ = O S T, ,
1( ) ( 1)1f x m xx
′ = − > −+
0
1( ) 0 1 1f x x m
′ = ⇒ = − > −
( )f x 11 1m
− − , 1 1 .m
− + ∞ ,
( ) ln ( 1)g x x m x m n= + + + + 1 1 1
2 2 2
( ) 0 ln ( 1) 0
( ) 0 ln ( 1) 0
g x x m x m n
g x x m x m n
= + + + + = ⇒ = + + + + =
, ,
,
1
1 2
1 2
2 1 2
ln
ln ( 1)( ) 0 1
x
x xm x x mx x x
+ + − = ⇒ + = − −
1 2 2
1
( 1)x x m
< +
2 2
21 2 1 1 2 1 2
1 2
2 1 2 1 2 2 1
2
( ) ( )ln 2
ln
x x x x x x xx x x x x x x x
x
− −< ⇔ < = − +
1 2x x< 1
2
(0 1)xt x
= ∈令 , 2 1ln 2t t t
< − + 2 1( ) ln 2g t t t t
= − − +
2
12ln1 1( ) 2 ln 1
t t tg t tt t t
− +
′ = − + = ,
1( ) 2lnh t t t t
= − +
2
2
( 1)( ) 0th t t
−′ = − < ( )h t (0 1), ( ) (1) 0h t h> = ( )g t (0 1),
( ) (1) 0g t g< = 2 1ln 2t t t
< − + (0 1)t ∈ ,
22.(本小题满分 10 分)解:(Ⅰ)因为 的直角坐标为 ,……(1 分)
设 的方程: ,将 代入得 ,
所以 的直角坐标方程为 , ……………………………………………(3 分)
化为极坐标方程: ………………………………………(5 分)
(Ⅱ)将 代入 得 ,
所以 ……………………………………………………(7 分)
又因为 ,所以 ,由①③得 ………………(8 分)
代入②有 ,所以 . ………………………………(10 分)
23.(本小题满分 10 分)【选修 4-5:不等式选讲】
(Ⅰ)解:当 时, ………………………(2 分)
当 时, ,无解;
当 时, ,解得 ,所以 ;
当 时, 恒成立,
所以 的解集为 . ……………………………………………(5 分)
(Ⅱ)证明:
当 时, , …………(7 分)
而
.
当且仅当 时,等号成立,即 ,
π2 3Q
, (1 3)Q ,
C 2 2 ( 0)y px p= > (1 3)Q , 3
2p =
C 2 3y x=
2sin 3cos .ρ θ θ=
1 cos
sin
x tl y t
α
α
= +
=
,: ,
2 3C y x=: 2 2sin 3 cos 3 0t tα α− − =
1 2 2
1 2 2
3cos
sin
3
sin
t t
t t
α
α
α
+ = − = ②,
①,
| | 2 | |PA PB= 1 22t t= − ③
1 2
2 2
6cos
sin
3cos
sin
t
t
α
α
α
α
= − =
,
,
2
4 2
18cos 3
sin sin
α
α α
− −= tan 6α =
2a =
5
( ) 2 3
5
f x x
= − +
−
,
,
,
1
1 4
4
x
x
x
−
− <
>
,
,
,
≤
≤
1x −≤ ( ) 5 1f x = ≤
1 4x− < ≤ ( ) 2 3 1f x x= − + ≤ 1x≥ 1 4x≤ ≤
4x > ( ) 5 1f x = − ≤
( ) 1f x ≤ [1 )+ ∞,
x∈R 2 2 2 2( ) | | | 1| | ( ) ( 1) | | 1| 1f x x a x x a x a a= − − + − − + = + = +≤
2 2 2 2 2 2 2+ 2 ( 1) 1b c a a b c a+ − + = + + −
2 2 2 2 2 21= ( + + + ) 12 a b b c c a+ + −
1 (2 2 2 ) 1 1 02 ab bc ac ab bc ac+ + − = + + − =≥
3
3a b c= = = 2 2 2 22 +1b c a a+ + ≥
因此,当 时, 得证. ………………………(10 分)x∈R 2 2 2 2( ) 1 2f x a b c a+ + +≤ ≤