【数学】江西省吉安市2019-2020学年高一下学期期末考试试题

【数学】江西省吉安市2019-2020学年高一下学期期末考试试题

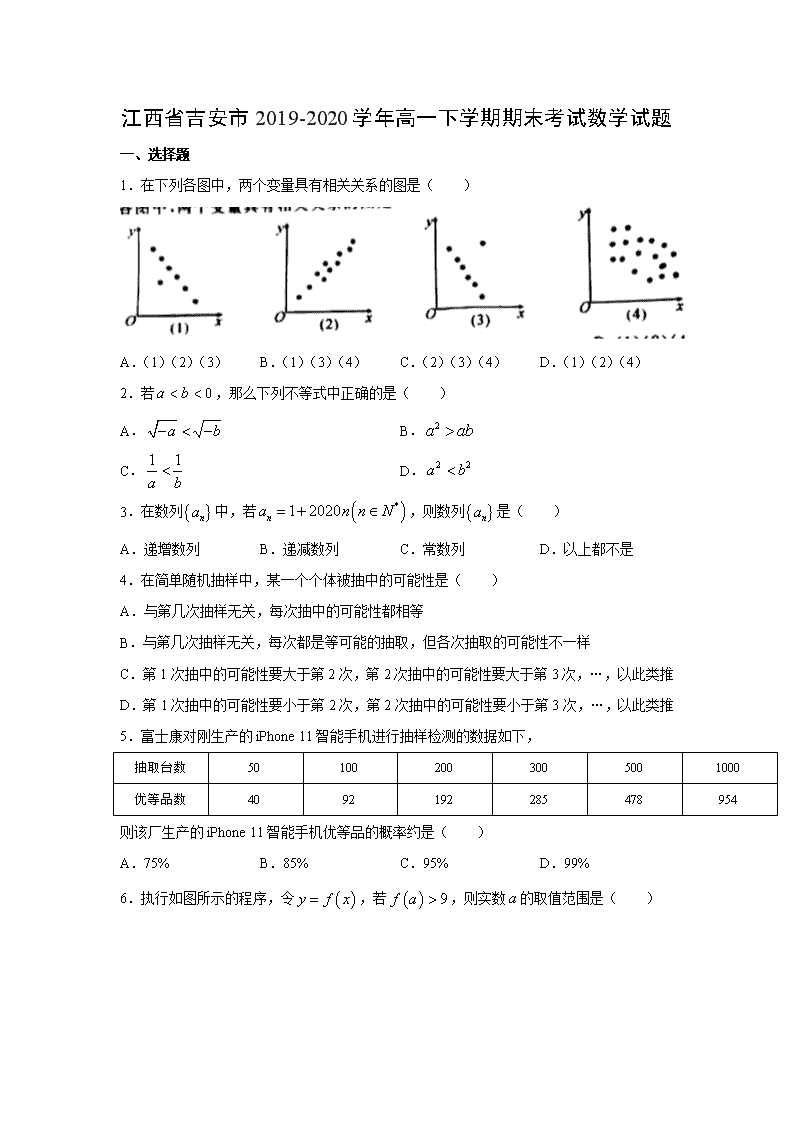
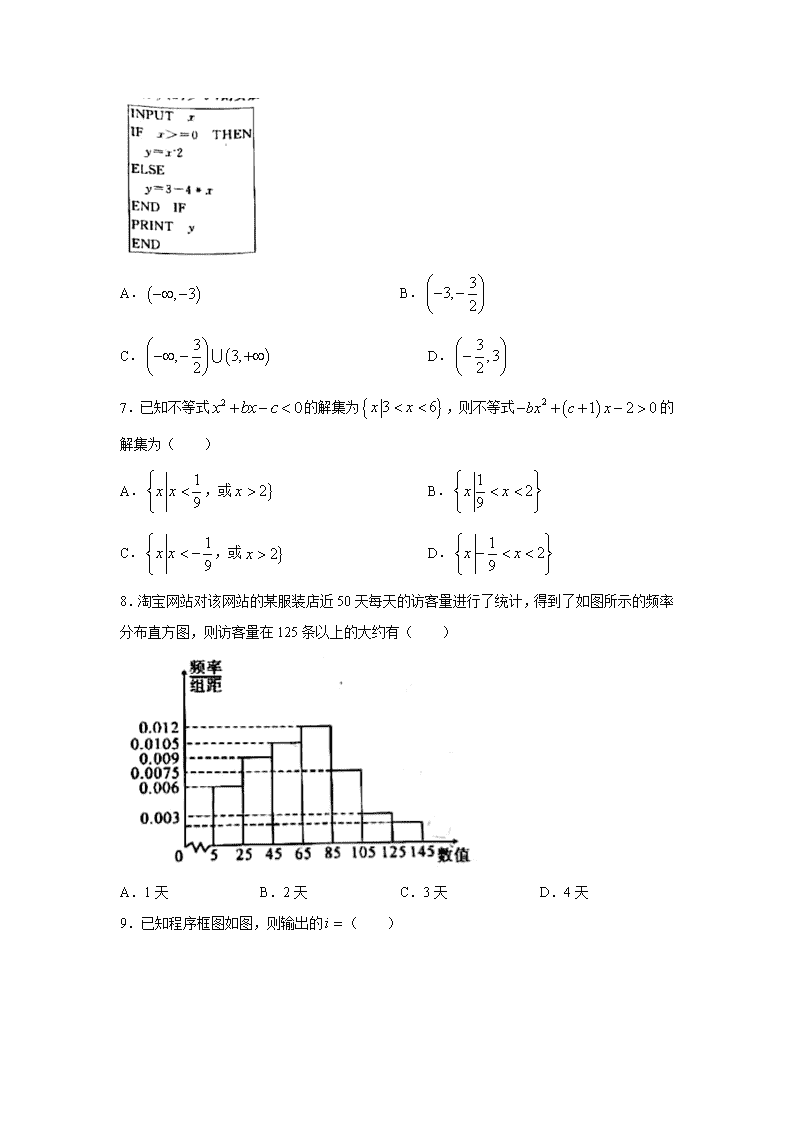
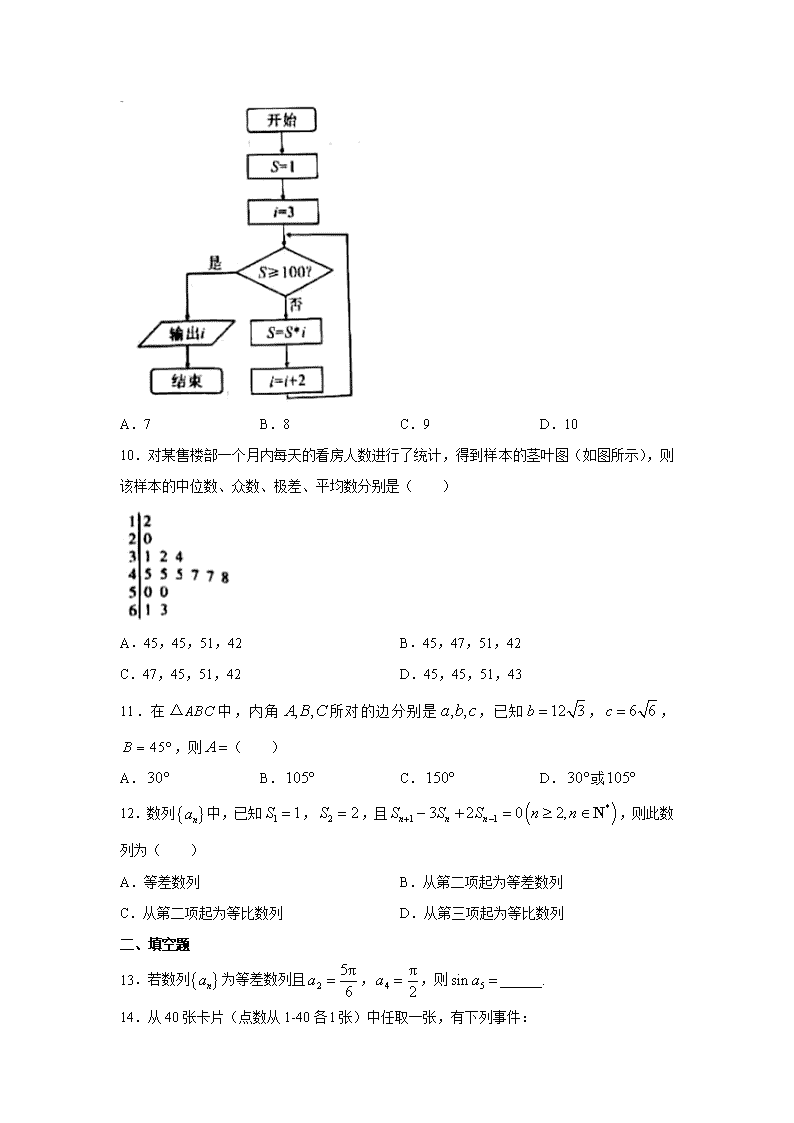
江西省吉安市2019-2020学年高一下学期期末考试数学试题 ‎ 一、选择题 ‎1．在下列各图中，两个变量具有相关关系的图是（ ）‎ A．（1）（2）（3） B．（1）（3）（4） C．（2）（3）（4） D．（1）（2）（4）‎ ‎2．若，那么下列不等式中正确的是（ ）‎ A． B．‎ C． D．‎ ‎3．在数列中，若，则数列是（ ）‎ A．递增数列 B．递减数列 C．常数列 D．以上都不是 ‎4．在简单随机抽样中，某一个个体被抽中的可能性是（ ）‎ A．与第几次抽样无关，每次抽中的可能性都相等 B．与第几次抽样无关，每次都是等可能的抽取，但各次抽取的可能性不一样 C．第1次抽中的可能性要大于第2次，第2次抽中的可能性要大于第3次，…，以此类推 D．第1次抽中的可能性要小于第2次，第2次抽中的可能性要小于第3次，…，以此类推 ‎5．富士康对刚生产的iPhone 11智能手机进行抽样检测的数据如下，‎ 抽取台数 ‎50‎ ‎100‎ ‎200‎ ‎300‎ ‎500‎ ‎1000‎ 优等品数 ‎40‎ ‎92‎ ‎192‎ ‎285‎ ‎478‎ ‎954‎ 则该厂生产的iPhone 11智能手机优等品的概率约是（ ）‎ A．75% B．85% C．95% D．99%‎ ‎6．执行如图所示的程序，令，若，则实数的取值范围是（ ）‎ A． B．‎ C． D．‎ ‎7．已知不等式的解集为，则不等式的解集为（ ）‎ A．，或 B．‎ C．，或 D．‎ ‎8．淘宝网站对该网站的某服装店近50天每天的访客量进行了统计，得到了如图所示的频率分布直方图，则访客量在125条以上的大约有（ ）‎ A．1天 B．2天 C．3天 D．4天 ‎9．已知程序框图如图，则输出的（ ）‎ A．7 B．8 C．9 D．10‎ ‎10．对某售楼部一个月内每天的看房人数进行了统计，得到样本的茎叶图（如图所示），则该样本的中位数、众数、极差、平均数分别是（ ）‎ A．45，45，51，42 B．45，47，51，42‎ C．47，45，51，42 D．45，45，51，43‎ ‎11．在中，内角所对的边分别是，已知，，，则（ ）‎ A． B． C． D．或 ‎12．数列中，已知，，且，则此数列为（ ）‎ A．等差数列 B．从第二项起为等差数列 C．从第二项起为等比数列 D．从第三项起为等比数列 二、填空题 ‎13．若数列为等差数列且，，则______.‎ ‎14．从40张卡片（点数从1-40各l张）中任取一张，有下列事件：‎ ‎①“抽出的牌点数小于10”与“抽出的牌点数大于20”；‎ ‎②“抽出的牌点数小于20”与“抽出的牌点数大于10”；‎ ‎③“抽出的牌点数是奇数”与“抽出的牌点数是偶数”；‎ ‎④“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”；‎ 其中，（1）是互斥事件的有______；‎ ‎（2）是对立事件的有______；‎ ‎（3）既不是对立事件，也不是互斥事件的有______.‎ ‎15．在中，内角所对的边分别是，已知，，则______.‎ ‎16．一个总体数为60的个体编号为00，01，02，…，59，现需从中抽取一个容量为7的样本，请从随机数表的倒数第5行（下表为随机数表的最后5行）第7~8列的22开始，依次向下，到最后一行后，再从下两列的上边开始，继续向下读，直到取足样本，则抽取样本的号码是______.‎ ‎95 33 95 22 00 18 74 72 00 18 46 40 62 98 80 54 97 20 56 95‎ ‎38 79 58 69 32 81 76 80 26 92 15 74 80 08 32 16 46 70 50 80‎ ‎82 80 84 25 39 90 84 60 79 80 67 72 16 42 79 71 59 73 05 50‎ ‎24 36 59 87 38 82 07 53 89 35 08 22 23 71 77 91 01 93 20 49‎ ‎96 35 23 79 18 05 98 90 07 35 82 96 59 26 94 66 39 67 98 60‎ 三、解答题 ‎17．已知，，，求的最小值.‎ ‎18．2020年，新冠病毒在世界肆虐，造成很多行业前景不如从前，国家最近调查了，，三类工种的复工情况，在调查的所有职工中，工种占40%，工种占50%，工种占10%.现用分层抽样的方法从调查的全体职工中抽取一个容量为的样本.‎ 试确定：‎ ‎（Ⅰ）若，则在工种、工种、工种中分别应抽取多少人？‎ ‎（Ⅱ）若抽取的工种比工种多30人，则抽取的工种有多少人？‎ ‎19．某校高二（21）班共有40名学生，他们的身高全部在162cm到187cm之间，按他们身高分5个组统计得到如下频率分布表：‎ 分组 频数 频率 ‎[162,167)‎ ‎4‎ ‎0.1‎ ‎[167,172)‎ ‎8‎ ‎[172,177)‎ ‎12‎ ‎0.3‎ ‎[177,182)‎ ‎10‎ ‎0.25‎ ‎[182,187)‎ ‎（Ⅰ）某兴趣小组为研兖每天体育锻炼的时间与身高的相关性，需要在这40名学生中按身商用分层抽样的方法抽取20名学生进行研究，问应抽取多少名笫一组的学生并求出表格中的，？‎ ‎（Ⅱ）已知第一组的学生中男、女生均为2人.在（Ⅰ）的条件下抽取第一组的学生，求既有男生又有女生被抽中的概率.‎ ‎20．已知公差不为0的等差数列中，且，，成等比数列.‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）若数列满足，求数列的前项和.‎ ‎21．随着快递业的发展，网购的流行，居民不出门通过网购就可以实现轻松购物，为了研究一般家庭月平均收入与月平均网购支出的关系，该市统计部门随机调查10个有网购经验的家庭，得数据如下：‎ 家庭编号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎（收入）千元 ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎（网购支出）千元 ‎0.1‎ ‎0.3‎ ‎0.4‎ ‎0.5‎ ‎0.6‎ ‎0.8‎ ‎1.0‎ ‎1.2‎ ‎1.4‎ ‎1.6‎ ‎（Ⅰ）判断家庭月平均收入与月平均网购支出是否相关？‎ ‎（Ⅱ）若家庭月平均收入与月平均网购支出两者线性相关，求回归直线方程.（保留三位小数）‎ 参考数据：，.‎ 参考公式：对于一组具有线性相关关系的数据，，…，，其回归直线的斜率和截距的最小二乘法估计分别为，.‎ ‎22．在中，角，，所对的边分别是，，，，.‎ ‎（Ⅰ）求角；‎ ‎（Ⅱ）若，求的 面积.‎ 参考答案 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A B A A C C C B C A B C ‎1．A【解析】（4）的散点图比较杂乱无章，不在一条直线附近，变量之间不具有相关关系，（1）（2）（3）散点图中的点大致分布在直线附近，所以具有线性相关关系，故选A.‎ ‎2．B【解析】对于A，由，得，所以，故A项错误；‎ 对于B，由两边同时乘以，得，故B项正确；‎ 对于C，由，得，故C项错误；‎ 对于D，由，得，故D项错误.故选A.‎ ‎3．A【解析】根据题意有，所以数列是递增数列.故选A.‎ ‎4．A【解析】不论先后，被抽取的概率都是，故选A.‎ ‎5．C【解析】该厂生产的iPhone11智能手机优等品的概率约是.故选C.‎ ‎6．C【解析】因为所以由，得或解得或.故实数的取值范围是.故选C.‎ ‎7．C【解析】由题意，的两根为3，6，则解得 则不等式可化为，解得，或.故选C.‎ ‎8．B【解析】因为访客量在125条以上的频率为 ‎，所以访客量在125条以上的大约有天.故选B.‎ ‎9．C【解析】第一次运行时，，；‎ 第二次运行时，，；‎ 第三次运行时，，；此时满足，故输出.故选C.‎ ‎10．A【解析】中位数为45，众数为45，极差为63－12=51，平均数为 ‎.故选A.‎ ‎11．B【解析】由正弦定理得，即，解得.因为，所以，则，故.故选B.‎ ‎12．C【解析】由，，得，，因为，所以，即，所以，所以，又不符合此式，因此数列从第二项起为等比数列.故选C.‎ ‎13．【解析】易知公差，则.所以.‎ ‎14．（1）①③；（2）③；（3）②④‎ ‎【解析】①互斥事件；②既不是对立事件，也不是互斥事件；③是对立事件；④既不是对立事件，也不是互斥事件，故是互斥事件的有①③，是对立事件的有③，既不是对立事件，也不是互斥事件的有②④.‎ ‎15．【解析】由，得，得，则由余弦定理得，解得.‎ ‎16．22，25，00，32，39，38，18‎ ‎【解析】先选取22，向下69不符合要求，下面选取25，向下87，79不符合要求，再从下两列的上边开始，继续向下读，00、32、39、38、18，因此，抽取的样本的号码是22，25，00，32，39，38，18.‎ ‎17．解：‎ ‎.‎ 当且仅当，即时取等号，故的最小值的最小值为25.‎ ‎18．解：（Ⅰ）工种应抽取的人数为，‎ 工种应抽取的人数为，‎ 工种应抽取的人数为，‎ ‎（Ⅱ）若抽取的工种比工种多30人，‎ 则，解得.‎ 故抽取的工种有人.‎ ‎19．解：（Ⅰ），.‎ 设应抽取名第一组的学生，则，解得.‎ 故应抽取2名第一组的学生.‎ ‎（Ⅱ）在（Ⅰ）的条件下应抽取2名第一组的学生.‎ 记第一组中2名男生，，2名女生为，.‎ 共有6种等可能的结果，列举如下：‎ ‎，，，，，.‎ 其中既有男生又有女生被抽中的有，，，这4种结果，‎ 所以既有男生又有女生被抽中的概率为.‎ ‎20．解：（Ⅰ）设等差数列的公差为，‎ 因为成等比数列，所以.‎ 则.①‎ 又由，得，②‎ 联立①②，解得，（舍去）或，.‎ 所以.‎ ‎（Ⅱ）由（Ⅰ）得，‎ 所以数列的前项和.‎ ‎21．解：（Ⅰ）作出散点图如下：‎ 观察发现各个数据对应的点都在一条直线附近，所以两者呈线性相关关系.‎ ‎（Ⅱ），‎ ‎，‎ 由公式得，‎ 则，‎ 所以回归方程 ‎22．解：（Ⅰ）因为，所以.‎ 由，得，得.‎ 所以或.‎ ‎（Ⅱ）由，，得，‎ 当时，‎ ‎，‎ 故；‎ 当时，，‎ 故.‎