- 2021-04-16 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年云南民族大学附属中学高二上学期10月月考数学(文)试题
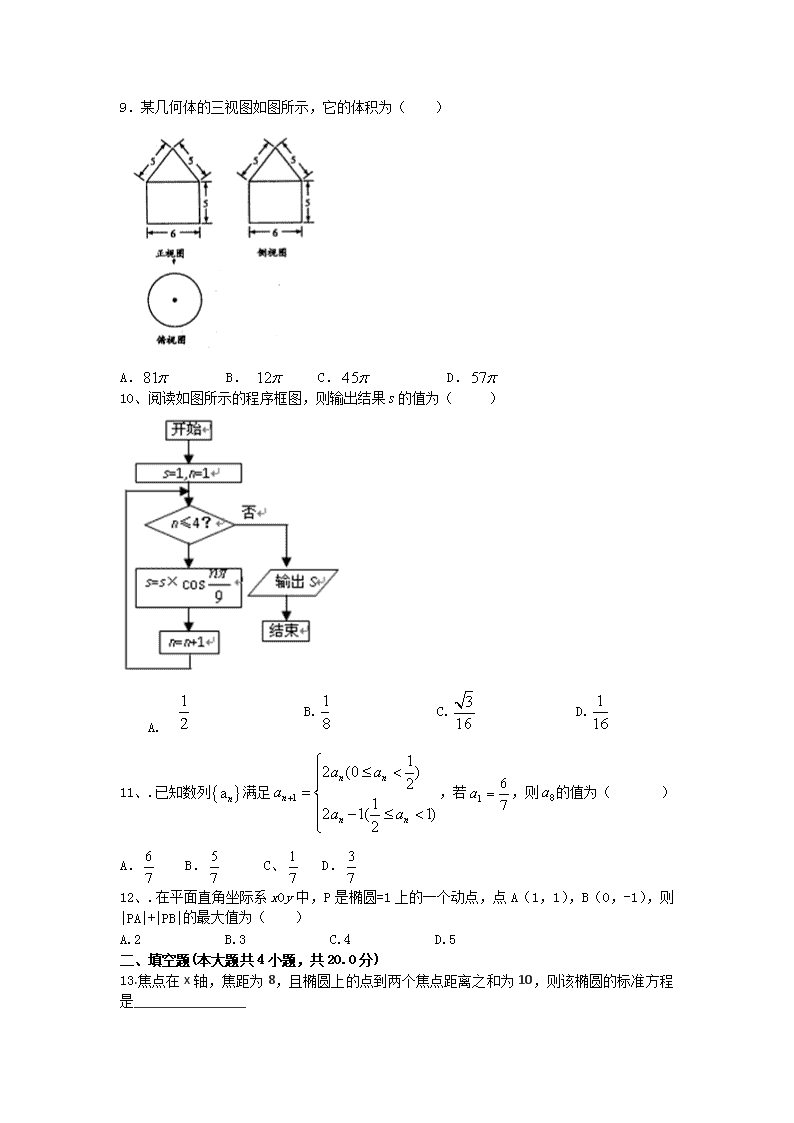
云南民族大学附属中学 2017年秋季学期10月月考高二(文科)数学试卷 (考试时间120分钟 满分150分) 注意事项: 1.答题前,考生务必用黑色碳素笔将自己的考号、姓名、考场、座位号、班级在答题卡上填写清楚。 2.本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。 一、选择题(每小题5分,共60分。下列每小题所给选项只有一项符合题意,请将正确答案的序号填涂在答题卡上) 1.实数集R,设集合P={},Q={},则P∪(∁RQ)=( ) A.[2,3] B.(1,3) C.(2,3] D.(-∞,-2]∪[1,+∞) 2.已知{an}为等差数列,,则等于( ) A.4 B.5 C.6 D.7 已知等比数列{an}满足,,则=( ) A.1 B. C. D.4 4、已知实数列成等比数列,则( ) A. B. C. D. 5、在5件产品中,其中一级品4件,二级品1件,从中任取2件,出现二级品的概率为( ) A. B. C. D. 6、为得到函数的图象, 只需要将函数的图象向( ) 个单位 A. 左平移 B. 右平移 C. 左平移 D. 右平移 7、椭圆的一个焦点为(0,1),则m=( ) A.1 B. C.-2或1 D.-2或1或 8、下列四个函数中,以π为最小正周期,且在区间(,π)上为减函数的是( ) A.y= B.y=sin2x C.y=2|cosx| D.y=cos 9.某几何体的三视图如图所示,它的体积为( ) A. B. C. D. 10、阅读如图所示的程序框图,则输出结果的值为( ) A. B. C. D. 11、.已知数列满足,若,则的值为( ) A. B. C、 D. 12、.在平面直角坐际系xOy中,P是椭圆=1上的一个动点,点A(1,1),B(0,-1),则|PA|+|PB|的最大值为( ) A.2 B.3 C.4 D.5 二、填空题(本大题共4小题,共20.0分) 13.焦点在x轴,焦距为8,且椭圆上的点到两个焦点距离之和为10,则该椭圆的标准方程是________________ 14. 函数恒过定点(1,3), 求的值为______. 15、已知函数的部分图象如下图所示,则函数的解析式为______________ 16. 设等差数列{an}、{bn}的前n项和分别为Sn、Tn,若对任意自然数n都有=,则+的值为________. 三、解答题(本大题共6小题,共70.0分) 17、(本小题满分10分)在△ABC中,设内角A、B、C的对边分别为a、b、c, (1)求角C的大小; (2)若且,求的面积. 18.(本小题12分)以下茎叶图记录了甲、乙两组各四名同学在某次数学测验中的成绩,甲组记录中有一个数据模糊,无法确认,在图中以X表示. 甲组 乙组 6 X 8 7 4 1 9 0 0 3 (1)如果甲组同学与乙组同学的平均成绩一样,求X及甲组同学数学成绩的方差; (2)如果X=7,分别从甲、乙两组同学中各随机选取一名,求这两名同学的数学成绩之和大于180的概率.(注:方差其中) 19、(本小题满分12分)已知Sn为等比数列{an}的前n项和•且S4=S3+3a3,a2=9. (1)求数列{an}的通项公式 (2)设bn=(2n-1)an,求数列{bn}的前n项和Tn. [] 20、(本题满分12分)已知直线l:y=x+m与圆C:x2+y2-2x+4y-4=0相交于A,B不同两点. (1)求m的取值范围; (2)设以AB为直径的圆经过原点,求直线l的方程. [] 21. (本小题共12分) F A1 D C B A B1 D1 C1 如图,直四棱柱ABCD – A1B1C1D1中,AB//CD,AD⊥AB,AB=2,AD=,AA1=3,E为CD上一点,DE=1,EC=3. (1)证明:BE⊥平面BB1C1C; (2)求点B1 到平面EA1C1 的距离. [] 22、(本题满分12分) 椭圆的对称中心在坐标原点,一个顶点为,右焦点F与点 的距离为2。 (1)求椭圆的方程; (2)斜率的直线与椭圆相交于不同的两点M,N满足,求直线l的方程。 2017年秋季学期10月月考高二数学答案 一、选择题、1-5DBBCD 6-10 CCADD 11-12 BD 二、填空题、13、 14、4 15、 16、 三、解答题 17 【答案】解:(Ⅰ) (Ⅱ) 18.(I)乙组同学的平均成绩为,甲组同学的平均成绩为90, 所以 甲组同学数学成绩的方差为 (II)设甲组成绩为86,87,91,94的同学分别为乙组成绩为87,90,90,93的同学分别为则所有的事件构成的基本事件空间为: 共16个基本事件. 设事件“这两名同学的数学成绩之和大于180”,则事件包含的基本事件的空间为{共7个基本事件, 19、解:(1)设等比数列{an}的公比为q, S4=S3+3a3,a2=9,可得 a4=S4-S3=3a3,即q==3, a1q=9,可得a1=3, 则数列{an}的通项公式为an=a1qn-1=3n; (2)bn=(2n-1)an=(2n-1)•3n; 则前n项和Tn=1•31+3•32+…+(2n-1)•3n; 3Tn=1•32+3•33+…+(2n-1)•3n+1; 两式相减可得,-2Tn=3+2(32+33+…+3n)-(2n-1)•3n+1 =3+2•-(2n-1)•3n+1; 化简可得Tn=3+(n-1)•3n+1. 20、(1)由,得:2x2+2(m+1)x+m2+4m-4=0,由此利用根的判别式能求出m的取值范围. (2)设A(x1,y1),B(x2,y2),则,由于以AB为直径的圆为(x-x1)(x-x2)+(y-y1)(y-y2)=0,若它经过原点,则x1x2+y1y2=0,由此能求出直线l的方 21.(文) (1)证明:过B作CD的垂线交CD于F,则 在 在,故 由 …………… 6分 (2) , 同理, 因此.设点B1到平面的距离为d,则 ,从而 …………… 12分 21、(理)解证:(1)因为平面, 平面 所以 , 又因为,,平面,, 所以平面 2分 又因为平面,平面, 所以 因为,,平面,, 所以 平面 4分 (2)因为⊥平面,又由(1)知, 建立如图所示的空间直角坐标系 .则,,,,, 设,,则 , 故点坐标为, 设平面的法向量为,则 所以 令,则. 10分 又平面的法向量 所以, 解得 故点为线段的中点. 12分[] 22、(1)依题意,设椭圆方程为,则其右焦点坐标为 ,由,得,即,解得。 又 ∵ ,∴ ,即椭圆方程为。 (4分) (2)方法一:由知点在线段的垂直平分线上,由消去得即 (*) ( 5分) 由,得方程(*)的,即方程(*)有两个不相等的实数根。 (6分) 设、,线段MN的中点,则,, ,即 ,∴直线的斜率为, (9分) 由,得,∴ ,解得:, (11分) ∴ l的方程为或。 ( 12分) 方法二:直线l恒过点(0,-2), 且点(0,-2)在椭圆上, ∴不妨设M(0,-2), 则|AM|=4 (6分) ∴|AN|=4, 故N在以A为圆心, 4为半径的圆上,即在的图像上. 联立 化简得 ,解得 (8分) 当y=-2时,N和M重合,舍去. 当y=0时,, 因此 (11分) ∴ l的方程为或。查看更多