- 2021-04-16 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级下数学教案人教八下数学课件17-1 勾股定理_人教新课标
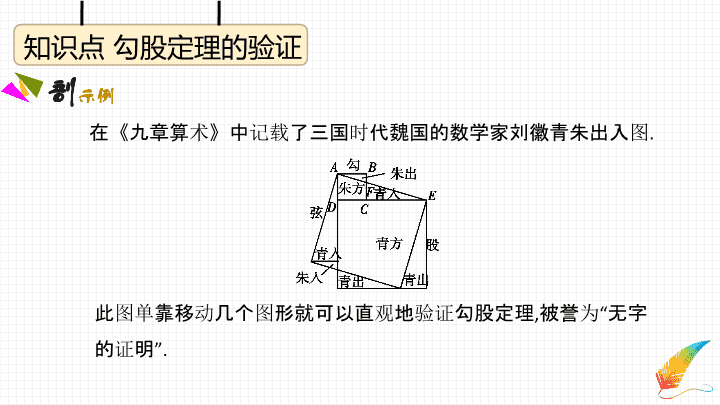
第十七章 勾股定理 17.1 勾股定理 知识点 勾股定理 1955年希腊发行了一张邮票,图案是由三个棋盘排列而成的.这张 邮票是纪念2500年前希腊一个学术和宗教团体——毕达哥拉斯 学派,它的成立以及在文化上的黄页,我们通过数格子的方法很容 易发现直角三角形三边之间的关系. 知识点 勾股定理的验证 在《九章算术》中记载了三国时代魏国的数学家刘徽青朱出入图. 此图单靠移动几个图形就可以直观地验证勾股定理,被誉为“无字 的证明”. 知识点 勾股定理在实际问题中的应用 少数人为了避开草地的拐角走“捷径”,他们仅仅就是为了少走几步 路(图中4 m),在草地内走出了一条“路”,却踩伤了草,三条路就组成 了直角三角形. 知识点 作长为 (n为大于1的整数)的线段 “勾股海螺” 知识点 作长为 (n为大于1的整数)的线段 作一条长度等于无理数的线段方法不唯一,尽量利用直角边长为整 数的直角三角形作出.另外要注意:并不是所有的无理数都能用尺 规作图的方法在数轴上作出对应的点,如π,0.1010010001……(相邻 两个1之间0的个数逐次加1)等. 第十七章 勾股定理 17.2 勾股定理的逆定理 知识点 互逆命题与互逆定理 公元前6世纪,古希腊哲人泰勒斯利用影子测量了金字塔的高度,他 自己还发现了三角形的一个特征:等腰三角形的两个底角相等,反 过来说,要使三角形两角相等,它们的对边必须相等.这个发现我们 现在看起来很简单,可是在当时发现它们的确不易,其实这两个三 角形的特征是互逆命题,或者说是互逆定理. 知识点 勾股定理的逆定理 古埃及人画直角的方法:把一根长绳打上等距离的13个结,然后以3 个结间距、4个结间距、5个结间距的长度为边长,用木桩就可以钉 成一个直角三角形.此三边的关系就可以判定直角三角形. 知识点 勾股数 神奇的三个台球号码,不但是连续的整数,还是一组勾股数.查看更多