- 2021-04-16 发布 |
- 37.5 KB |
- 6页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级数学下册知能提升作业二十八第20章平行四边形的判定20
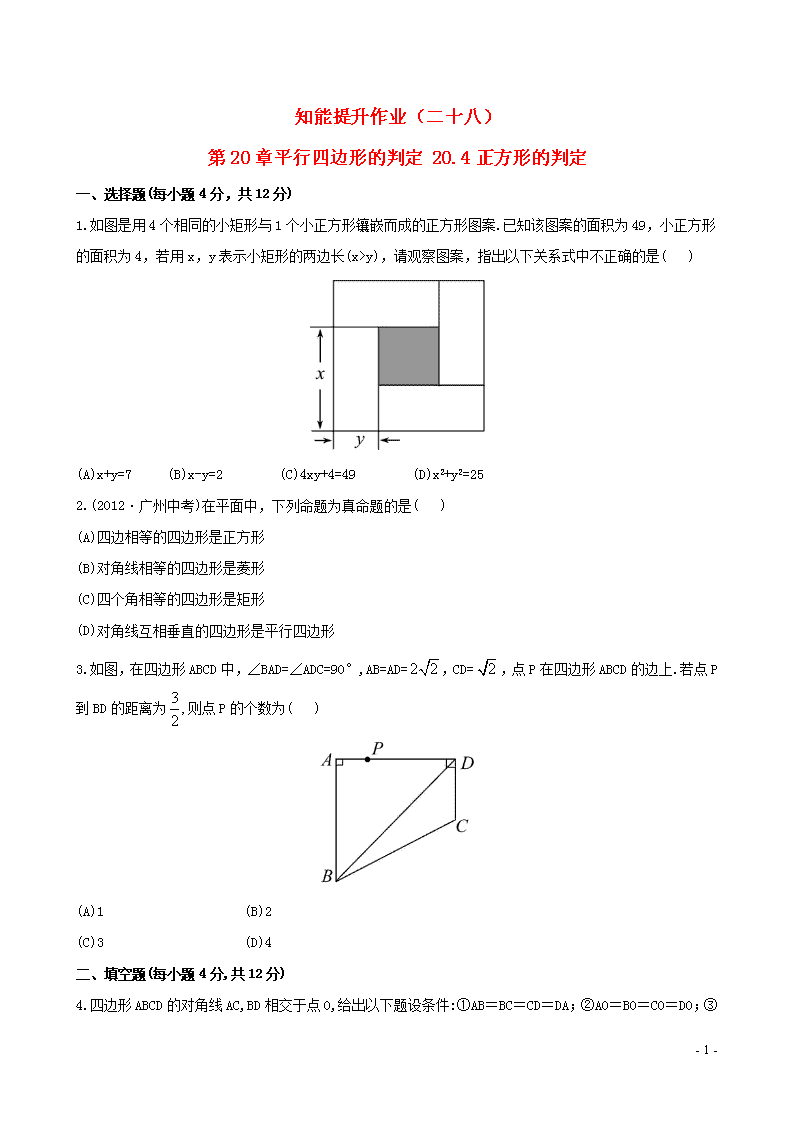
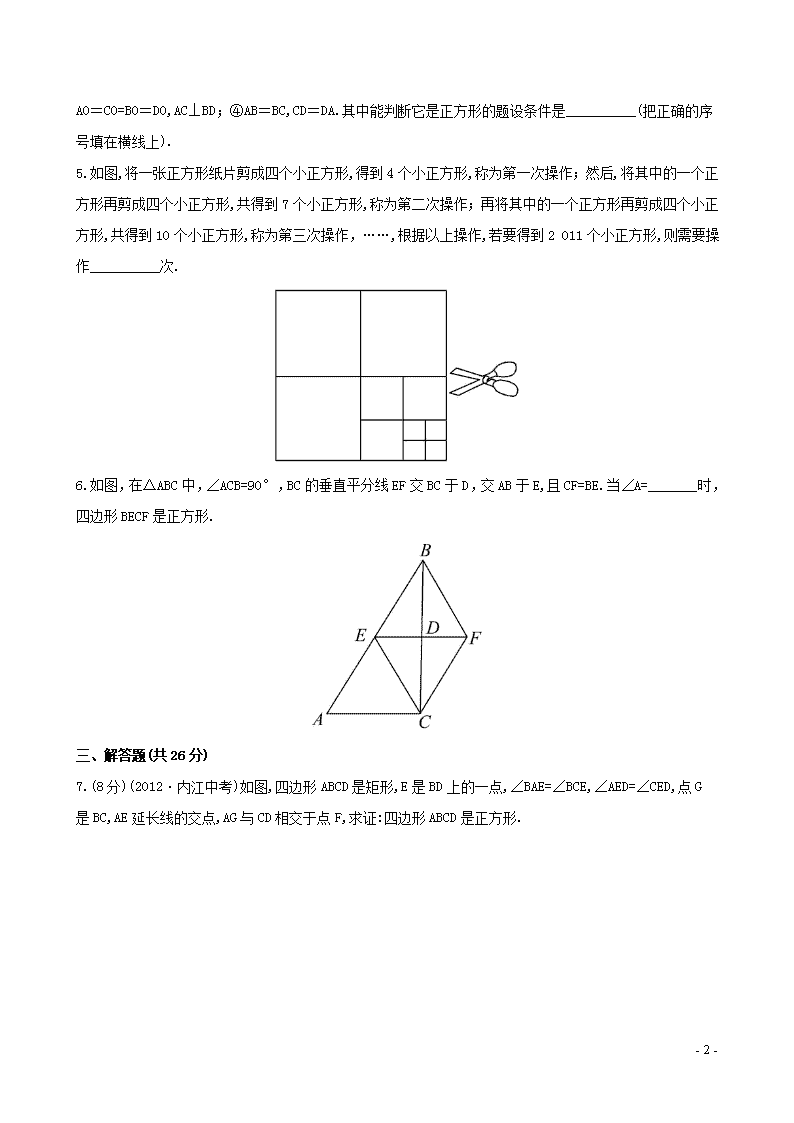
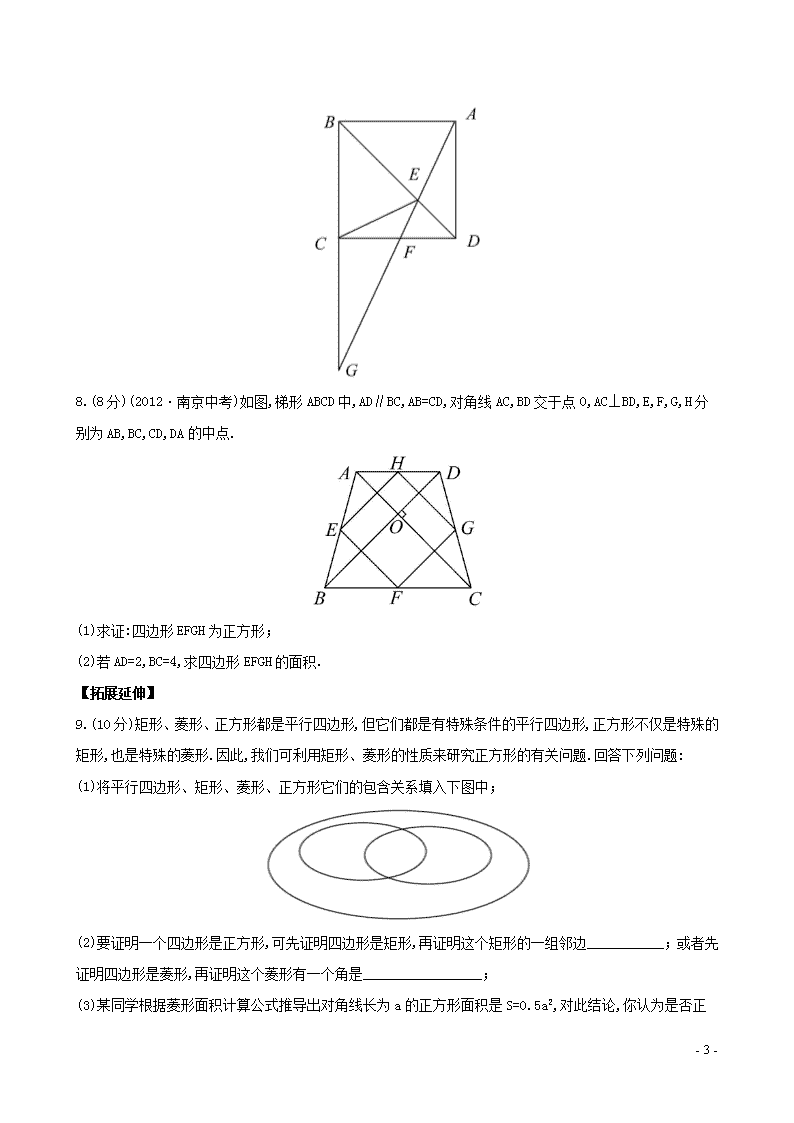
知能提升作业(二十八) 第20章平行四边形的判定 20.4正方形的判定 一、选择题(每小题4分,共12分) 1.如图是用4个相同的小矩形与1个小正方形镶嵌而成的正方形图案.已知该图案的面积为49,小正方形的面积为4,若用x,y表示小矩形的两边长(x>y),请观察图案,指出以下关系式中不正确的是( ) (A)x+y=7 (B)x-y=2 (C)4xy+4=49 (D)x2+y2=25 2.(2012·广州中考)在平面中,下列命题为真命题的是( ) (A)四边相等的四边形是正方形 (B)对角线相等的四边形是菱形 (C)四个角相等的四边形是矩形 (D)对角线互相垂直的四边形是平行四边形 3.如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=,CD=,点P在四边形ABCD的边上.若点P到BD的距离为则点P的个数为( ) (A)1 (B)2 (C)3 (D)4 二、填空题(每小题4分,共12分) 4.四边形ABCD的对角线AC,BD相交于点O,给出以下题设条件:①AB=BC=CD=DA;②AO=BO=CO=DO;③ - 6 - AO=CO=BO=DO,AC⊥BD;④AB=BC,CD=DA.其中能判断它是正方形的题设条件是__________(把正确的序号填在横线上). 5.如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作,……,根据以上操作,若要得到2 011个小正方形,则需要操作__________次. 6.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于D,交AB于E,且CF=BE.当∠A=_______时,四边形BECF是正方形. 三、解答题(共26分) 7.(8分)(2012·内江中考)如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC,AE延长线的交点,AG与CD相交于点F,求证:四边形ABCD是正方形. - 6 - 8.(8分)(2012·南京中考)如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC,BD交于点O,AC⊥BD,E,F,G,H分别为AB,BC,CD,DA的中点. (1)求证:四边形EFGH为正方形; (2)若AD=2,BC=4,求四边形EFGH的面积. 【拓展延伸】 9.(10分)矩形、菱形、正方形都是平行四边形,但它们都是有特殊条件的平行四边形,正方形不仅是特殊的矩形,也是特殊的菱形.因此,我们可利用矩形、菱形的性质来研究正方形的有关问题.回答下列问题: (1)将平行四边形、矩形、菱形、正方形它们的包含关系填入下图中; (2)要证明一个四边形是正方形,可先证明四边形是矩形,再证明这个矩形的一组邻边___________;或者先证明四边形是菱形,再证明这个菱形有一个角是_________________; (3)某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=0.5a2 - 6 - ,对此结论,你认为是否正确?若正确,请说明理由;若不正确,请举出一个反例说明. 答案解析 1.【解析】选D.大正方形的面积为49,边长x+y=7;小正方形的面积为4,边长x-y=2.四个小矩形的面积4xy加上小正方形的面积等于大正方形的面积,即4xy+4=49. 2.【解析】选C.根据平行四边形,矩形,菱形,正方形的判定定理,选项C正确. 3.【解析】选B.过点B作DC延长线的垂线相交于点E,由于∠A=∠ADC=∠E=90°,且AB=AD.所以,四边形ABED为正方形.又即C为DE中点.作CF⊥BD,F为垂足,设CF=DF=x,则解得x=1,即CF=1.又因为正方形的对角线所以当P点在AB、AD上时,P点到BD的距离可以为 4.【解析】由①得四边形是菱形;由②得四边形是矩形;由③得四边形是正方形;由④得四边形为一般四边形. 答案:③ 5.【解析】根据题意,知第一次操作得4=3+1(个),第二次操作得7=2×3+1(个),第三次操作得10=3×3+1(个),……,即第n次操作得(3n+1)(个),当3n+1=2 011时,解得n=670. 答案:670 6.【解析】∵EF垂直平分BC, ∴BE=EC,BF=CF. ∵CF=BE,∴BE=EC=CF=BF. ∴四边形BECF是菱形. 当∠A=45°时,△ABC为等腰直角三角形, - 6 - ∴∠ABC=45°, ∴∠ECB=∠ABC=45°, ∴∠ECF=90°,∴菱形BECF为正方形. 答案:45° 7.【证明】∵∠AED=∠CED,∴∠AEB=∠CEB. 又∵∠BAE=∠BCE,BE=BE, ∴△ABE≌△CBE,∴AB=CB. 又∵四边形ABCD是矩形, ∴四边形ABCD是正方形. 8.【解析】(1)在△ABC中,E,F分别是AB,BC的中点, 故可得同理 在梯形ABCD中,AB=DC,故AC=BD. ∴EF=FG=GH=HE, ∴四边形EFGH是菱形. 设AC与EH交于点M, 在△ABD中,E,H分别是AB,AD的中点, 则EH∥BD,同理GH∥AC, 又∵AC⊥BD,∴∠BOC=90°, ∴∠EHG=∠EMC=90°, ∴四边形EFGH是正方形. (2)连结EG. 在梯形ABCD中, ∵E,G分别是AB,DC的中点, - 6 - 在Rt△EHG中, ∵EH2+GH2=EG2,EH=GH, ∴即四边形EFGH的面积为 9.【解析】(1) (2)相等 直角 (3)正确.设菱形的两条对角线分别为a,b,则它的面积为S=0.5ab,当两条对角线相等时,这个四边形就为正方形,可得正方形的面积是0.5a2. - 6 -查看更多