- 2021-04-15 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
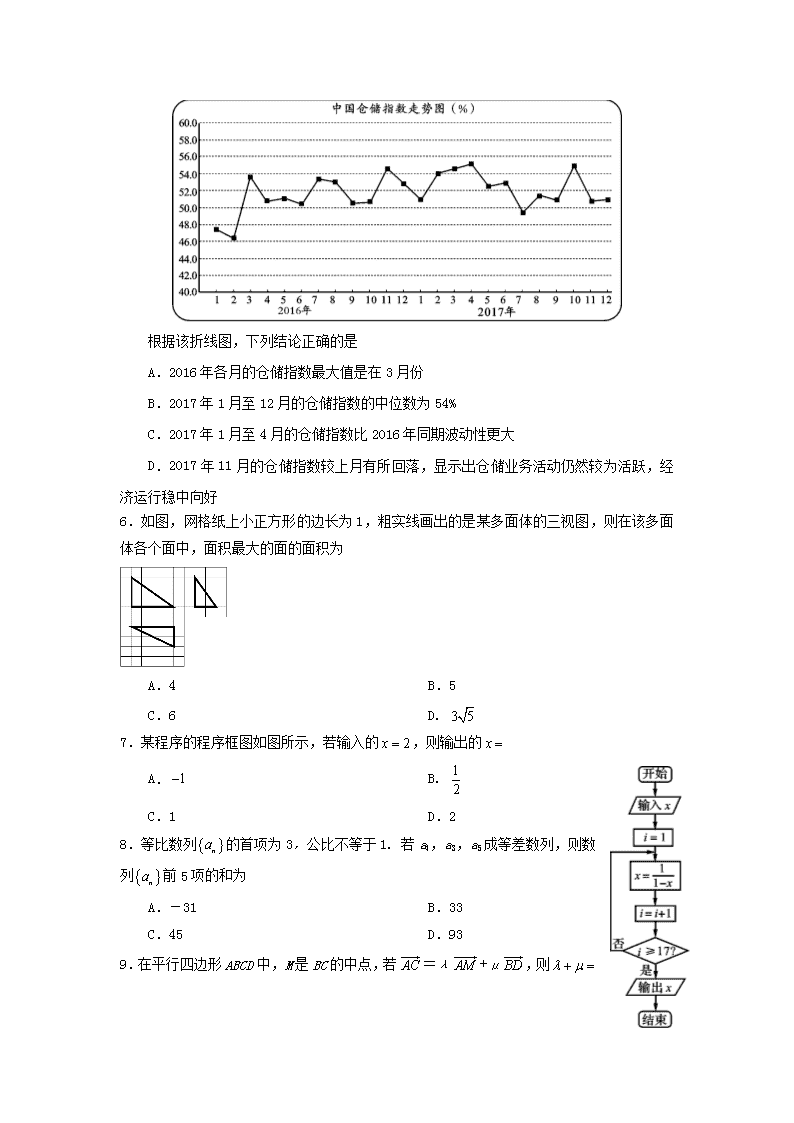
数学理卷·2018届四川省资阳市高三4月模拟考试(三诊)(2018
资阳市高中2015级(2018届)高考模拟考试 理科数学 注意事项: 1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。 2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。 3.考试结束后,将本试卷和答题卡一并交回。 一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。 1.设集合,,则 A. B. C. D. 2.复数z满足,则 A. B. C. D. 3.直线l:kx-y-2k=0与双曲线x2-y2=2仅有一个公共点,则实数k的值为 A.-1或1 B.-1 C.1 D.1,-1,0 4.已知角α的顶点与原点O重合,始边与x轴的正半轴重合,若它的终边经过点,则 A. -7 B. C. D. 7 5.为了反映国民经济各行业对仓储物流业务的需求变化情况,以及重要商品库存变化的动向,中国物流与采购联合会和中储发展股份有限公司通过联合调查,制定了中国仓储指数.如图所示的折线图是2016年1月至2017年12月的中国仓储指数走势情况. 根据该折线图,下列结论正确的是 A.2016年各月的仓储指数最大值是在3月份 B.2017年1月至12月的仓储指数的中位数为54% C.2017年1月至4月的仓储指数比2016年同期波动性更大 D.2017年11月的仓储指数较上月有所回落,显示出仓储业务活动仍然较为活跃,经济运行稳中向好 6.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则在该多面体各个面中,面积最大的面的面积为 A.4 B.5 C.6 D. 7.某程序的程序框图如图所示,若输入的,则输出的 A. B. C.1 D.2 8.等比数列的首项为3,公比不等于1. 若a4,a3,a5成等差数列,则数列前5项的和为 A.-31 B.33 C.45 D.93 9.在平行四边形ABCD中,M是BC的中点,若=λ+μ,则 A. B.2 C. D. 10. 从0,1,2,3这4个数字中选3个数字组成没有重复数字的三位数,则该三位数能被3整除的概率为 A. B. C. D. 11.如图,二面角的大小为,,且,,则AD与β所成角的大小为 A. B. C. D. 12.已知定义在R上的偶函数(函数f(x)的导函数为)满足,e3f(2018)=1,若,则关于x的不等式的解集为 A. B. C. D. 二、填空题:本大题共4小题,每小题5分,共20分。 13. 展开式中常数项为10,则实数__________. 14.已知实数满足则的最大值为_________. 15.等差数列的前n项和为,若,且,则公差的取值范围是________. 16. 抛物线的焦点为F,为抛物线上的两点,以为直径的圆过点F,过AB的中点作抛物线的准线的垂线,垂足为,则的最大值为________. 三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。 (一)必考题:共60分。 17.(12分) 在中,角A,B,C的对边分别为a,b,c,且. (1)求A. (2)若,求的取值范围. 18.(12分) 某超市计划销售某种食品,现邀请甲、乙两个商家进场试销10天.两个商家提供的返利方案如下:甲商家每天固定返利60元,且每卖出一件食品商家再返利3元;乙商家无固定返利,卖出30件以内(含30件)的食品,每件食品商家返利5元,超出30件的部分每件返利8元.经统计,两个商家的试销情况茎叶图如下: 甲 乙 8 9 9 8 9 9 2 8 9 9 2 0 1 0 3 2 1 1 1 0 1 0 (1)现从甲商家试销的10天中抽取两天,求这两天的销售量都小于30的概率; (2)若将频率视作概率,回答以下问题: ① 记商家乙的日返利额为X(单位:元),求X的分布列和数学期望; ② 超市拟在甲、乙两个商家中选择一家长期销售,如果仅从日平均返利额的角度考虑,请利用所学的统计学知识为超市作出选择,并说明理由. 19.(12分) 如图,三棱柱的各棱长均相等,底面,E,F分别为棱的中点. (1)过作平面α,使得直线BE//平面α,若平面α与直线交于点H,指出点H所在的位置,并说明理由; (2)求二面角的余弦值. 20.(12分) 已知为椭圆E:的左、右顶点,,E的两个焦点与E的短轴两个端点所构成的四边形是正方形. (1)求椭圆E的方程; (2)设动点(),记直线与E的交点(不同于)到x轴的距离分别为,求的最大值. 21.(12分) 已知函数(其中). (1)当时,求零点的个数k的值; (2)在(1)的条件下,记这些零点分别为,求证:. (二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。 22.[选修4-4:坐标系与参数方程](10分) 在平面直角坐标系中,直线的参数方程为(其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为. (1)写出直线l普通方程和曲线C的直角坐标方程; (2)过点且与直线平行的直线交于,两点,求. 23. [选修4-5:不等式选讲](10分) 已知函数. (1)解不等式; (2)若正实数a,b满足,试比较与的大小,并说明理由. 资阳市高中2015级高考模拟考试 理科数学参考答案及评分意见 一、选择题:本大题共12小题,每小题5分,共60分。 1.C 2.B 3.A 4.A 5.D 6.D 7.A 8.B 9.D 10.C 11.C 12.B 二、填空题:本大题共5小题,每小题4分,共20分。 13. 2;14. 3;15. ;16.. 三、解答题:共70分。 (一)必考题:共60分。 17.(12分) (1)根据正弦定理得,即, 则,即, 由于, 所以. 6分 (2)根据余弦定理,, 所以, 则有,又, 所以的取值范围是. 12分 18.(12分) (1)记“抽取的两天销售量都小于30”为事件A, 则P(A)==. 4分 (2)①设乙商家的日销售量为a,则 当a=28时,X=28×5=140; 当a=29时,X=29×5=145; 当a=30时,X=30×5=150; 当a=31时,X=30×5+1×8=158; 当a=32时,X=30×5+2×8=166; 所以X的所有可能取值为:140,145,150,158,166. 6分 所以X的分布列为 X 140 145 150 158 166 P 所以EX=140×+145×+150×+158×+166×=152.8 8分 ②依题意,甲商家的日平均销售量为:28×0.2+29×0.4+30×0.2+31×0.1+32×0.1=29.5 所以甲商家的日平均返利额为:60+29.5×3=148.5元. 10分 由①得乙商家的日平均返利额为152.8元(>148.5元), 所以推荐该超市选择乙商家长期销售. 12分 19.(12分) (1)如图所示,平面FHA1即为平面α,H点为线段BB1的中点. 2分 理由如下: 因为直线BE//平面α,平面α∩平面AB1=A1H,直线BEÌ平面AB1, 所以直线BE//直线A1H,又A1E//直线BH, 所以四边形BEA1H是平行四边形,则BH= A1E, 即H点为BB1的中点. 4分 (2)如图,取B1C1的中点Q,显然FC,FQ,FA两两互相垂直,建立如图所示的空间直角坐标系F-xyz如图所示. 不妨设棱长为2,则H(-1,1,0),A1(0,2,), 则,, 设面FHA1的法向量, 则由得 令,得. 取平面BFH的一个法向量, 于是. 所以二面角的余弦值为. 12分 20.(12分) (1)由得,则. 因为E的两个焦点与E的短轴两个端点所构成的四边形是正方形. 所以,又,解得, 故椭圆E的方程为. 4分 (2)不妨设.直线的方程为,直线的方程为, 设, 由得,可得. 6分 又由得,可得. 8分 则. 因为,当且仅当取等号,则, 即.当且仅当取等号. 12分 21.(12分) (1)由题x>0,,则, 由得, 当x>时,,为增函数;当0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档