江苏省南菁高级中学2019届高三上学期周练（9

江苏省南菁高级中学2019届高三上学期周练（9

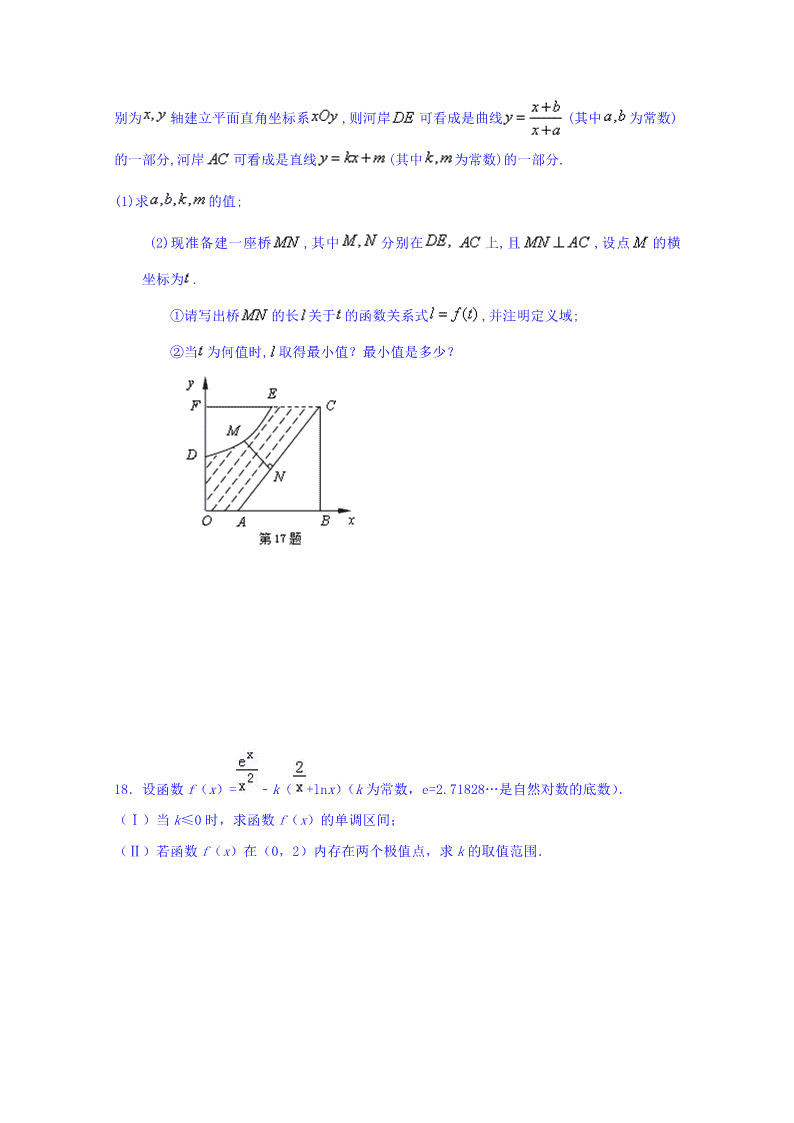
南菁高中 2019 届高三数学(文)周测试卷(三)2018.9.22 卷面满分 130 分 测试时间 90 分钟 一、填空题(5 分*14=70 分) 1.设集合 , ,则 ▲ ． 2.函数 的定义域为 ▲ ． 3.函数 y＝ax(a>0，a≠1)在区间[0，1]上的最大值与最小值之和为 3，则实数 a 的值为 ▲ ． 4.已知角α的顶点与原点重合，始边与 x 轴的正半轴重合，终边上一点的坐标为(3，4)，则 cos 2α＝ ▲ ． 5.若函数 y＝sin(ωx－φ) π 2 在区间 π ，π上的图象如图所示， 则φ的值分别是 ▲ ． 6.已知 sin π 3 ＝ 1 3，则 sin 5π －x－cos π 3 的值为 ▲ ． 7.已知 x>0，y>0，x＋3y＋xy＝9，则 x＋3y 的最小值为 ▲ ． 8.已知函数 是定义在 上的单调增函数,且对于一切实数 x,不等式 恒成立,则实数 b 的取值范围是 ▲ ． 9.已知实数 x，y 满足 x＋y－5≥0， y－4≤0. 若不等式 4x2＋y2－axy≤0 恒成立，则实数 a 的最小值为 ▲ ． 10.定义在 上的奇函数 ,当 时, 则函数 的所有零点之和为 ▲ ． 11.已知函数 f（x）=﹣ x2﹣3x+4lnx 在[t，t+1]上不单调，则实数 t 的取值范围是 ▲ ． 12.设 f′(x)和 g′(x)分别是函数 f(x)和 g(x)的导函数，若 f′(x)·g′(x)≤0 在区间 I 上 恒成立，则称函数 f(x)和 g(x)在区间 I 上单调性相反．若函数 f(x)＝ 1 3x3－2ax 与函数 g(x) ＝x2＋2bx 在开区间(a，b)(a＞0)上单调性相反，则 b－a 的最大值等于 ▲ ． 13.在锐角三角形 ABC 中，若 sin A＝2sin Bsin C，则 tan Atan Btan C 的最小值是 ▲ ． 14.已知正实数 a，b，c 满足 1 a＋ 1 b＝1， 1 ab＋ 1 bc＋ 1 ca＝1，则实数 c 的取值范围是 ▲ ． 二、解答题(共 60 分,请将解答过程写在答卷纸指定位置.) 15. 已知函数 f(x)＝2cos2x＋2sin xcos x. (1) 求函数 f(x)的最小正周期； (2) 在△ABC 中，若 f(C)＝2，2sin B＝cos(A－C)－cos (A＋C)，求 tan A 的值． 16．函数 f（x）和 g（x）的图象关于原点对称，且 f（x）=x2+2x （Ⅰ）求函数 g（x）的解析式； （Ⅱ）解不等式 g（x）≥f（x）﹣|x﹣1|． （Ⅲ）若 h（x）=g（x）﹣λf（x）+1 在[﹣1，1]上是增函数，求实数λ的取值范围． 17. 如图,河的两岸分别有生活小区 和 ,其中 , , , 三点共线, 与 的延长线交于点 ,测得 , , , , . 若以 所在直线分 别为 轴建立平面直角坐标系 ,则河岸 可看成是曲线 (其中 为常数) 的一部分,河岸 可看成是直线 (其中 为常数)的一部分. (1)求 的值; (2)现准备建一座桥 ,其中 分别在 上,且 ,设点 的横 坐标为 . ①请写出桥 的长 关于 的函数关系式 ,并注明定义域; ②当 为何值时, 取得最小值？最小值是多少？ 18．设函数 f（x）= ﹣k（ +lnx）（k 为常数，e=2.71828…是自然对数的底数）． （Ⅰ）当 k≤0 时，求函数 f（x）的单调区间； （Ⅱ）若函数 f（x）在（0，2）内存在两个极值点，求 k 的取值范围．