- 2021-04-15 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
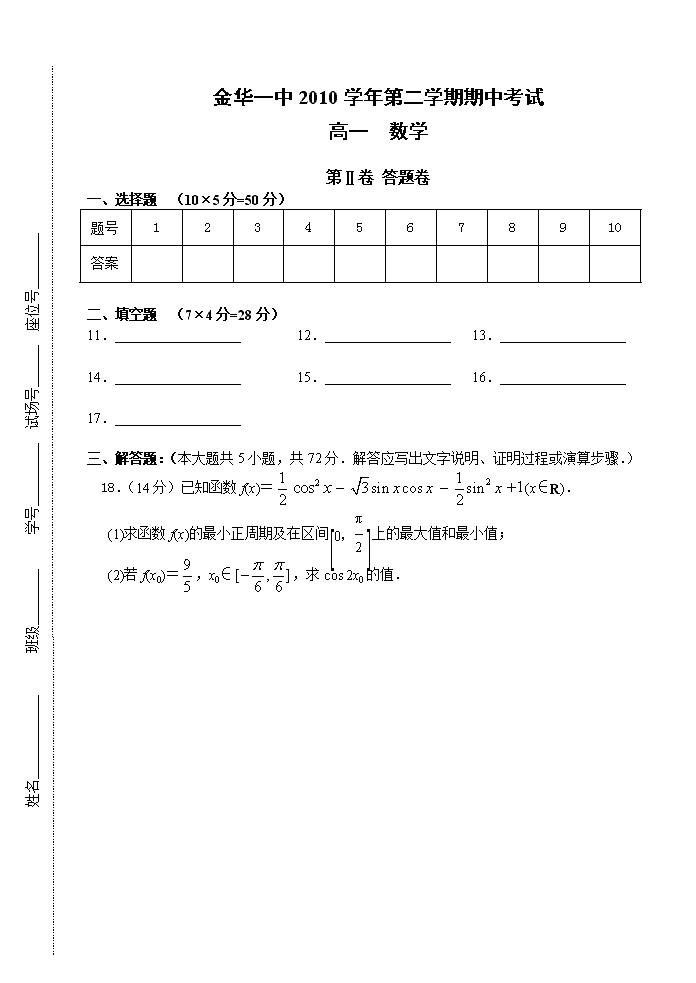
浙江省金华一中10-11学年高一数学下学期期中试题新人教A版
金华一中2010学第二学期期中考试高一 数学 本试卷分为第Ⅰ卷和第Ⅱ卷两部分.全卷共六页,第Ⅰ卷1至2页为选择填空部分.第Ⅱ卷3至6页为答题卷.满分150分,考试时间120分种.注意:答案写在答题卷上有效. 第Ⅰ卷 一、 选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.的值为 ( ) A. B. C. D. 2.向量=(1,-2),||=4||,且、共线,则可能是 ( ) A.(4,8) B.(-4,8) C.(-4,-8) D.(8,4) 3.函数的一个单调增区间是 ( ) A.() B.() C.() D.() 4.在是 ( ) A.直角三角形 B.钝角三角形 C. 等腰三角形 D.等边三角形 5.若在直线上存在不同的三点A、B、C,使得关于实数的方程有解(O点不在上),则此方程的解集为 ( ) A.{-1} B. C., D.{-1,0} 6.已知角的终边经过点(,)(),则的值为( ) A.1或 B.或 C.1或 D. 或 7. 函数y=Asin(wx+j)(w>0,A¹0)的图象与函数y=Acos(wx+j)(w>0, A¹0)的图象在区间(,+)上 ( ) A.至少有两个交点 B.至多有两个交点 C.至多有一个交点 D.至少有一个交点 8. 在三角形ABC中,AB=,BC=2,A=,如果不等式 恒成立,则实数的取值范围是 ( ) A.[1,+) B.[] C.(-][1,+ ) D. (-][1,+ ) 9.曲线和直线=在y轴右侧的交点按横坐标从小到大依次记为…,则等于 ( ) A.p B.2p C.3p D.4p 10. 已知等腰直角△ABC,∠B=90°,AB=2,点M是△ABC内部或边界上一动点,N是边BC的中点,则的最大值为 ( ) A.4 B.5 C.6 D.7 二、填空题:(本大题共7小题,每小题4分,共28分.) 11.若=1,=,=0,则与的夹角为__________________。 12._______________。 13.已知13sin+5cos=9,13cos+5sin=15,那么sin(+)的值为________________。 14.已知向量,,则的值为______________。 15.在中,AC=4,BC=5,cos(AB)=,则cosC=________________。 16.设,,利用三角变换,估计在时的取值情况,猜想对取一般值时的取值范围是________________。 17.给出下列说法: 存在实数,使; 若是锐角三角形的内角,则; 为了得到函数y=sin的图象,只需把函数y=sin的图象向右平移个长度单位; 函数的最小正周期为; 在中,若,则A=B。其中正确说法的序号是 。 姓名____________ 班级________ 学号_________ 试场号 座位号 金华一中2010学年第二学期期中考试 高一 数学 第Ⅱ卷 答题卷 一、选择题 (105分=50分) 题号 1 2 3 4 5 6 7 8 9 10 答案 二、填空题 (74分=28分) 11.__________________ 12.__________________ 13.__________________ 14.__________________ 15.__________________ 16.__________________ 17.__________________ 三、解答题:(本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.) 18.(14分)已知函数f(x)=(x∈R). (1)求函数f(x)的最小正周期及在区间上的最大值和最小值; (2)若f(x0)=,x0∈,求cos 2x0的值. 19.(14分) 已知点是 且 (1)设实数t满足=0,求t的值; (2)试用,表示。 20.(14分)中,AD是BC边上的高,垂足为D点。BE是ABC的角平分线,并交AC于E点。若BC=6,CA=7,AB=8。 (1) 求DE的长; (2)求的面积。 21.(14分) 设向量,,。其中,,。与的夹角为,与的夹角为,当时,求的值。 22.(16分) 已知函数,,() (1)问取何值时,方程在上有两解; (2)若对任意的,总存在,使成立,求实数的取值范围? 金华一中2010学年第二学期期中考试 高一 数学 一、选择题 (105分=50分) 题号 1 2 3 4 5 6 7 8 9 10 答案 B B A D A B C C A C 二、填空题 (74分=28分) 11. 12. -1 13. 14.1 15. 16.17. 三、解答题:(本大题共5小题,共72分.) 21.(14分) 22.(16分) (1) 化为在上有两解 换 则在上解的情况如下: ①当在上只有一个解或相等解,有两解或 ∴或 ②当时,有惟一解 ③当时,有惟一解 故 或 (2)当 ∴值域为 当时,则 有 ①当时,值域为 ②当时,值域为 而依据题意有的值域是值域的子集 则 或 ∴或 查看更多