- 2021-04-15 发布 |
- 37.5 KB |
- 2页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019九年级数学上册 第二十三章 23关于原点对称的点的坐标
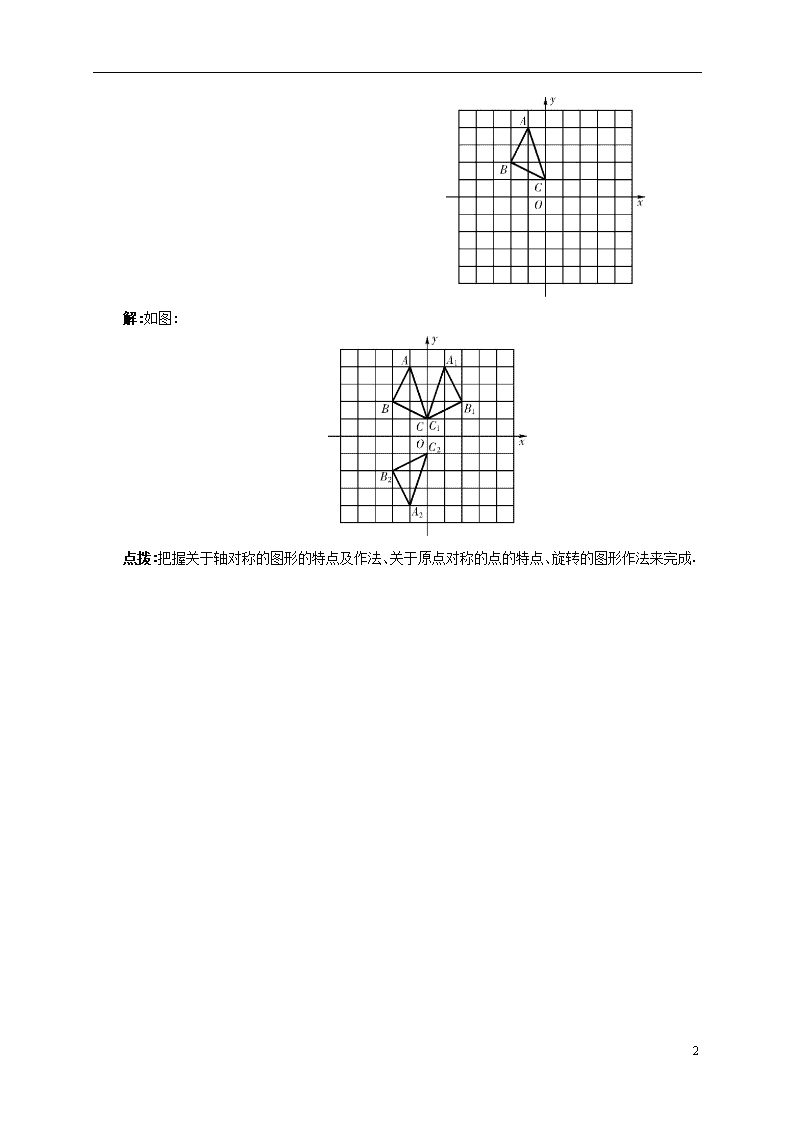
第二十三章 23.2.3关于原点对称的点的坐标 知识点1:关于原点对称的点的坐标 在坐标平面内,点P(x,y)关于原点对称的点P'的坐标为(-x,-y). 归纳整理:(1)两个点关于原点对称时,它们的坐标符号相反,第一象限的点关于原点对称的点在第三象限,第二象限的点关于原点对称的点在第四象限,坐标轴上的点关于原点对称的点仍在坐标轴上. (2)关于坐标轴对称和关于原点对称的区别:关于x轴对称,横坐标不变,纵坐标互为相反数,即点P(x,y)关于x轴对称的点的坐标为(x,-y);关于y轴对称,横坐标互为相反数,纵坐标不变,即点P(x,y)关于y轴对称的点的坐标为(-x,y);关于原点对称,横、纵坐标都互为相反数,即点P(x,y)关于原点对称的点的坐标为(-x,-y). 知识点2:坐标与变换 平移、旋转、轴对称的简单作图以网格或直角坐标系为背景,借助点的坐标的变换引起图形的变换.关键是要弄清变换方向、角度、距离等,此类作图通常是以关键点的坐标的变换带动图形的变换,即以局部带动整体进行作图. 考点:坐标系内的对称问题 【例】 △ABC在平面直角坐标系中的位置如图所示,将△ABC沿y轴翻折得到△A1B1C1,再将△A1B1C1绕点O旋转180°得到△A2B2C2.请依次画出△A1B1C1和△A2B2C2. 2 解:如图: 点拨:把握关于轴对称的图形的特点及作法、关于原点对称的点的特点、旋转的图形作法来完成. 2查看更多