- 2021-04-15 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
西藏拉萨中学2020届高三上学期第三次月考数学(理)试卷
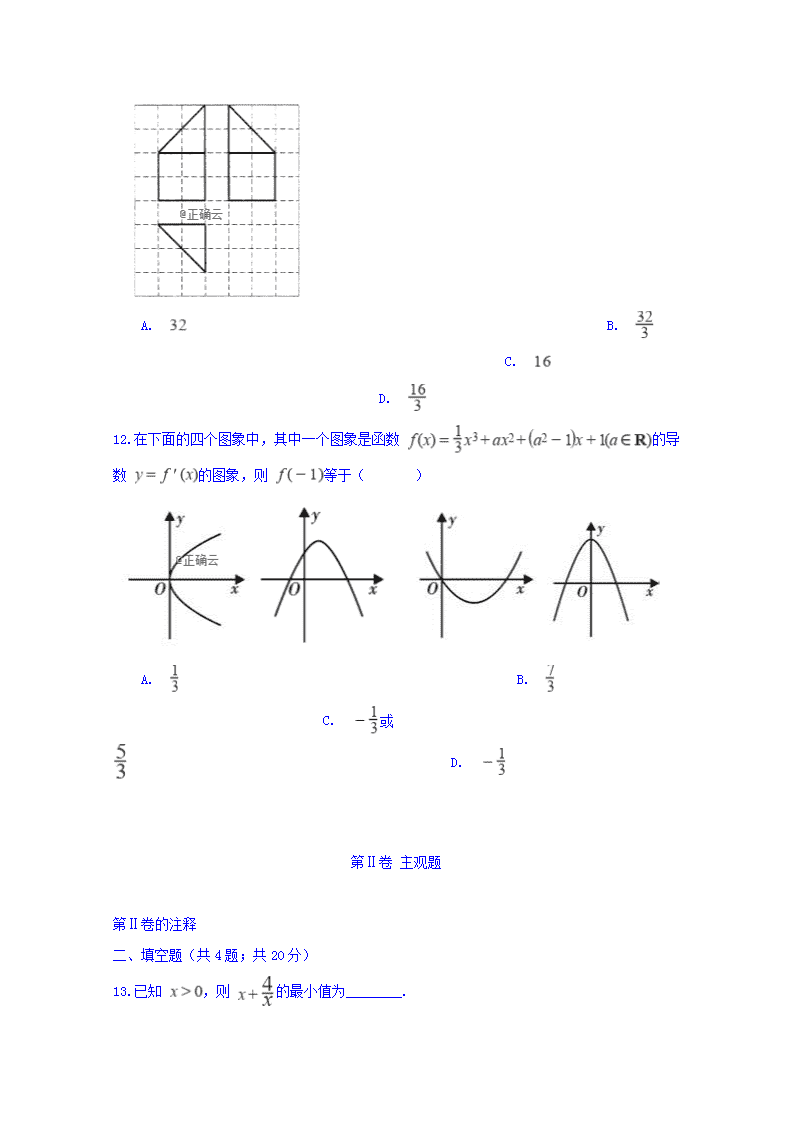
理科数学试卷 第Ⅰ卷 客观题 第Ⅰ卷的注释 一、单选题(共12题;共60分) 1.已知集合U= ,A= ,B= 则 =( ) A. B. C. D. 2.已知向量 , 且 ,则 ( ) A. B. C. D. 3.在等差数列 中, ,则 ( ) A. 32 B. 45 C. 64 D. 96 4.若 , , ,则 的大小关系是( ) A. B. C. D. 5.在 中,角 的对边分别为 .已知 ,则 ( ) A. B. C. D. 6.等比数列 的各项均为正数,且 ,则 A. 12 B. 8 C. 10 D. 7.曲线y=﹣x3+3x2在点(1,2)处的切线方程为( ) A. y=3x﹣1 B. y=﹣3x+5 C. y=3x+5 D. y=2x 8.设函数 ,则满足 的x的取值范围是 A. B. C. D. 9.已知等差数列的前n项为Sn , 且a1+a5=-14,S9=-27,则使得Sn取最小值时的n为( ) A. 1 B. 6 C. 7 D. 6或7 10.在明朝程大位《算法统宗》中有这样的一首歌谣:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头(最少一层)几盏灯?”( ) A. 6 B. 5 C. 4 D. 3 11.如图,网格纸上小正方形的边长为 ,粗实线画出的是某几何体的三视图,则该几何体的体积为( ) A. B. C. D. 12.在下面的四个图象中,其中一个图象是函数 的导数 的图象,则 等于( ) A. B. C. 或 D. 第Ⅱ卷 主观题 第Ⅱ卷的注释 二、填空题(共4题;共20分) 13.已知 ,则 的最小值为________. 14.已知 满足约束条件: ,则 的最大值是________. 15.记Sn为等差数列的前n项和,若 ,则 ________. 16.给出下列四个命题: ① 中, 是 成立的充要条件; ②当 时,有 ;③已知 是等差数列 的前n项和,若 ,则 ;④若函数 为 上的奇函数,则函数 的图象一定关于点 成中心对称.其中所有正确命题的序号为________. 三、解答题(共计70分) 17.(12分)已知,数列是等差数列,满足=2,,数列是等比数列,满足 (1)求数列和的通项公式; (2)求数列的前n项和Sn; 18.(12分)已知向量 = (1,2sinθ), = (sin(θ+ ),1),θ R。 (1)若 ⊥ ,求 tanθ的值; (2)若 ∥ ,且 θ (0, ),求 θ的值 19.(12分)等差数列 中, . (1)求 的通项公式; (2)设 ,求数列 的前 项和 . 20.(12分)设函数 。 (1)求函数 的单调减区间; (2)若函数 在区间 上的极大值为8,求在区间 上的最小值。 21.(12分)已知函数 , . (1)若 为偶函数,求 的值并写出 的增区间; (2)若关于 的不等式 的解集为 ,当 时,求 的最小值; (3)对任意的 , ,不等式 恒成立,求实数 的取值范围. 22.(10分)证明不等式: (1)用分析法证明:> (2)已知、、为不全相等的实数, 求证: >查看更多