- 2021-04-15 发布 |
- 37.5 KB |
- 2页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人民教育出版版高考数学选修4123圆的切线的性质及判定定理随堂练习
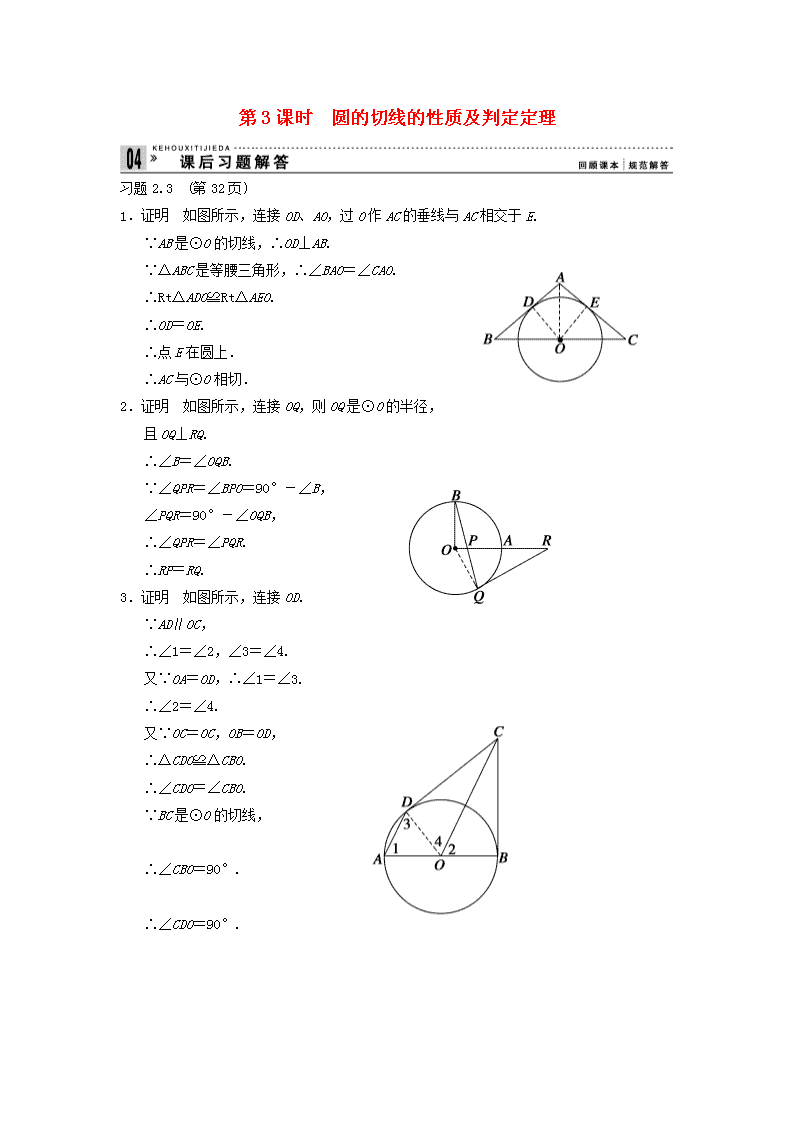
第3课时 圆的切线的性质及判定定理 习题2.3 (第32页) 1.证明 如图所示,连接OD、AO,过O作AC的垂线与AC相交于E. ∵AB是⊙O的切线,∴OD⊥AB. ∵△ABC是等腰三角形,∴∠BAO=∠CAO. ∴Rt△ADO≌Rt△AEO. ∴OD=OE. ∴点E在圆上. ∴AC与⊙O相切. 2.证明 如图所示,连接OQ,则OQ是⊙O的半径, 且OQ⊥RQ. ∴∠B=∠OQB. ∵∠QPR=∠BPO=90°-∠B, ∠PQR=90°-∠OQB, ∴∠QPR=∠PQR. ∴RP=RQ. 3.证明 如图所示,连接OD. ∵AD∥OC, ∴∠1=∠2,∠3=∠4. 又∵OA=OD,∴∠1=∠3. ∴∠2=∠4. 又∵OC=OC,OB=OD, ∴△CDO≌△CBO. ∴∠CDO=∠CBO. ∵BC是⊙O的切线, ∴∠CBO=90°. ∴∠CDO=90°. ∴DC是⊙O的切线.查看更多