- 2021-04-15 发布 |
- 37.5 KB |
- 3页


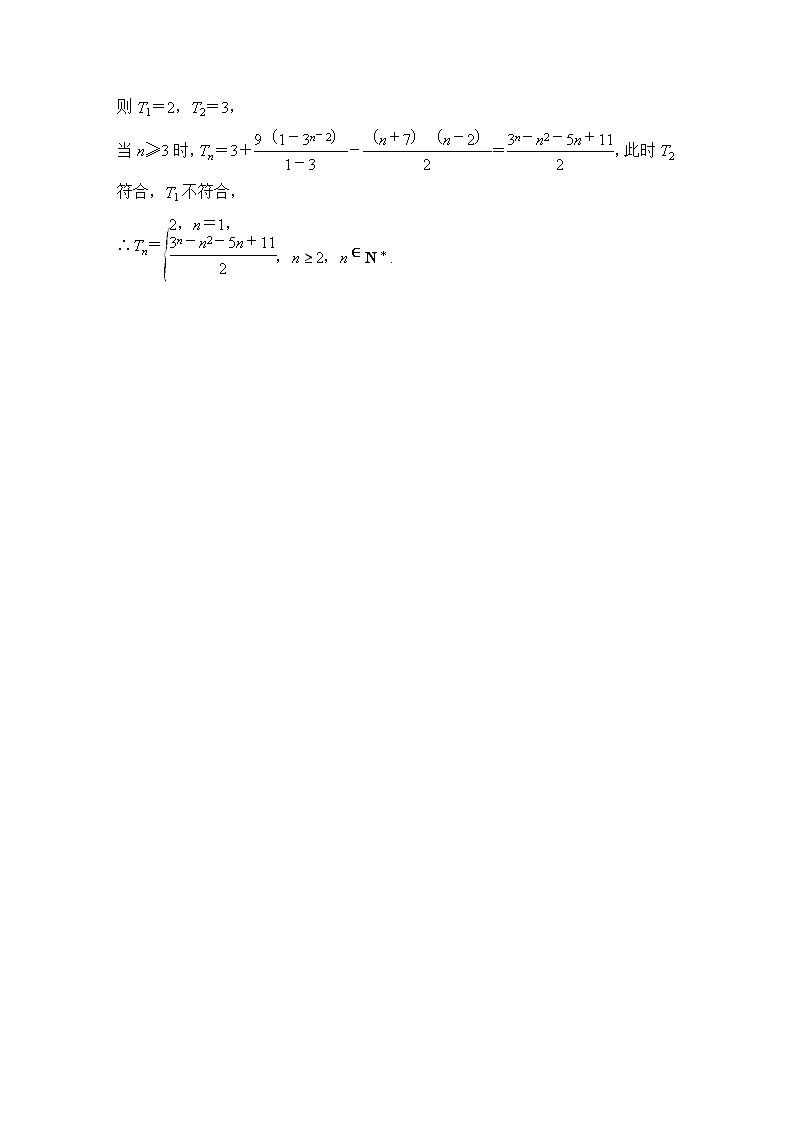
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习模板 数列问题学案(全国通用)
模板3 数列问题 (满分15分)已知{an}是公差为3的等差数列,数列{bn}满足b1=1,b2=,anbn+1+bn+1=nbn. (1)求{an}的通项公式;(2)求{bn}的前n项和. 满分解答 得分说明 解题模板 解 (1)由已知,a1b2+b2=b1,b1=1,b2=, ∴a1=2, (3分) 所以数列{an}是首项为2,公差为3的等差数列, (6分) 因此{an}的通项公式an=2+3(n-1)=3n-1. (7分) ①牢记等差、等比数列的定义:在判断数列为等差或等比数列时,应根据定义进行判断,所以熟练掌握定义是解决问题的关键,如本题第(2)问,要根据定义判断=. ②注意利用第(1)问的结果:在题设条件下,如果第(1)问的结果第(2)问能用得上,可以直接用,有些题目不用第(1)问的结果甚至无法解决,如本题即是在第(1)问的基础上求得bn+1与bn的关系. 第一步:将n=1代入关系式anbn+1+bn+1=nbn,求出a1的值; 第二步:利用等差数列的通项公式求出an; 第三步:将第(1)问中求得的an代入关系式anbn+1+bn+1=nbn,求得bn+1与bn的关系; 第四步:判断数列{bn}为等比数列; 第五步:代入等比数列的前n项和公式求Sn. 第六步:反思检验,规范解题步骤. (2)由(1)和anbn+1+bn+1=nbn, 得bn+1==≠0,则=, (11分) 因此数列{bn}是首项为1,公比为的等比数列, (12分) 设数列{bn}的前n项和为Sn,则 Sn==-. (15分) ③写全得分关键:写清解题过程的关键点,有则给分,无则没有分,同时解题过程中计算准确,是得分的根本保证.如本题第(1)问要写出a1b2+b2=b1,b1=1,b2=,才能得出a1,并指出数列{an}的性质,否则不能得全分.第(2)问中一定要写出求bn+1=的步骤并要指明{bn}的性质;求Sn时,必须代入求和公式而不能直接写出结果,否则要扣分. 【训练3】 (2016·浙江卷)设数列{an}的前n项和为Sn,已知S2=4,an+1=2Sn+1,n∈N*. (1)求通项公式an; (2)求数列{|an-n-2|}的前n项和. 解 (1)由题意得则 又当n≥2时,由an+1-an=(2Sn+1)-(2Sn-1+1)=2an,得an+1=3an,同时a2=3a1, ∴数列{an}的通项公式为an=3n-1,n∈N*. (2)设bn=|3n-1-n-2|,n∈N*,则b1=2,b2=1. 当n≥3时,由于3n-1>n+2, 故bn=3n-1-n-2,n≥3. 设数列{bn}的前n项和为Tn, 则T1=2,T2=3, 当n≥3时,Tn=3+-=,此时T2符合,T1不符合, ∴Tn=查看更多