- 2021-04-15 发布 |
- 37.5 KB |
- 3页
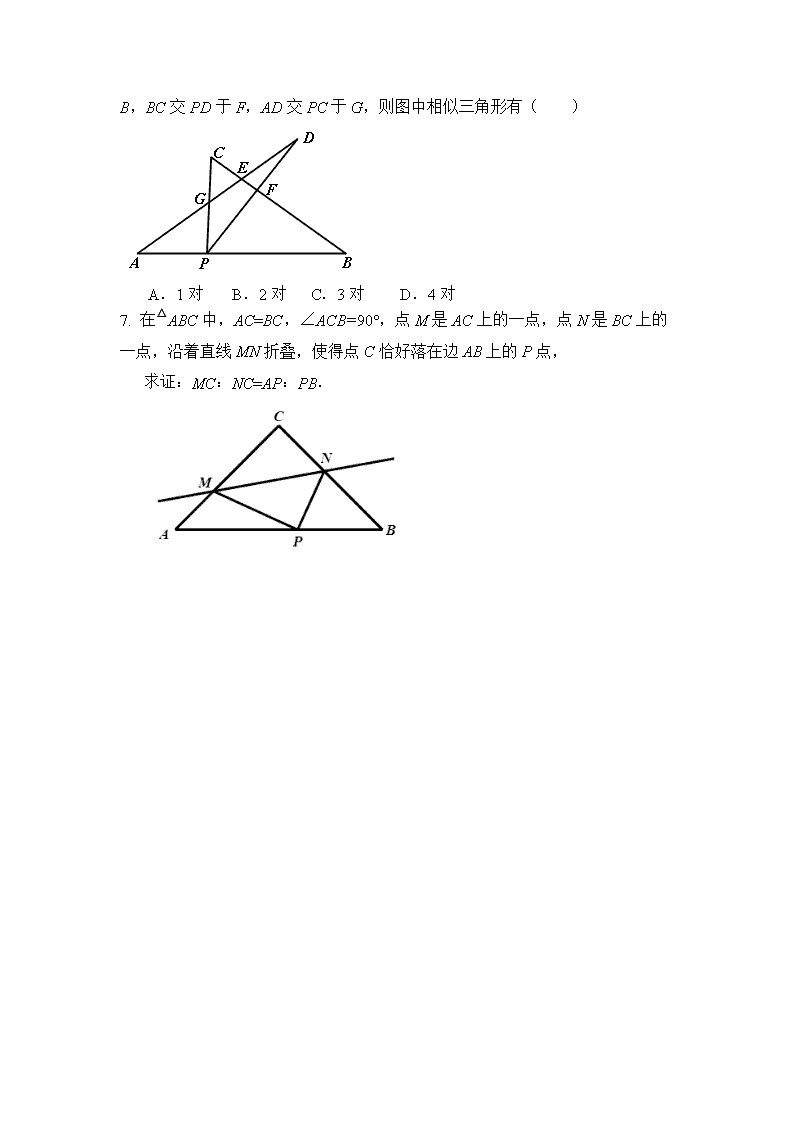
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
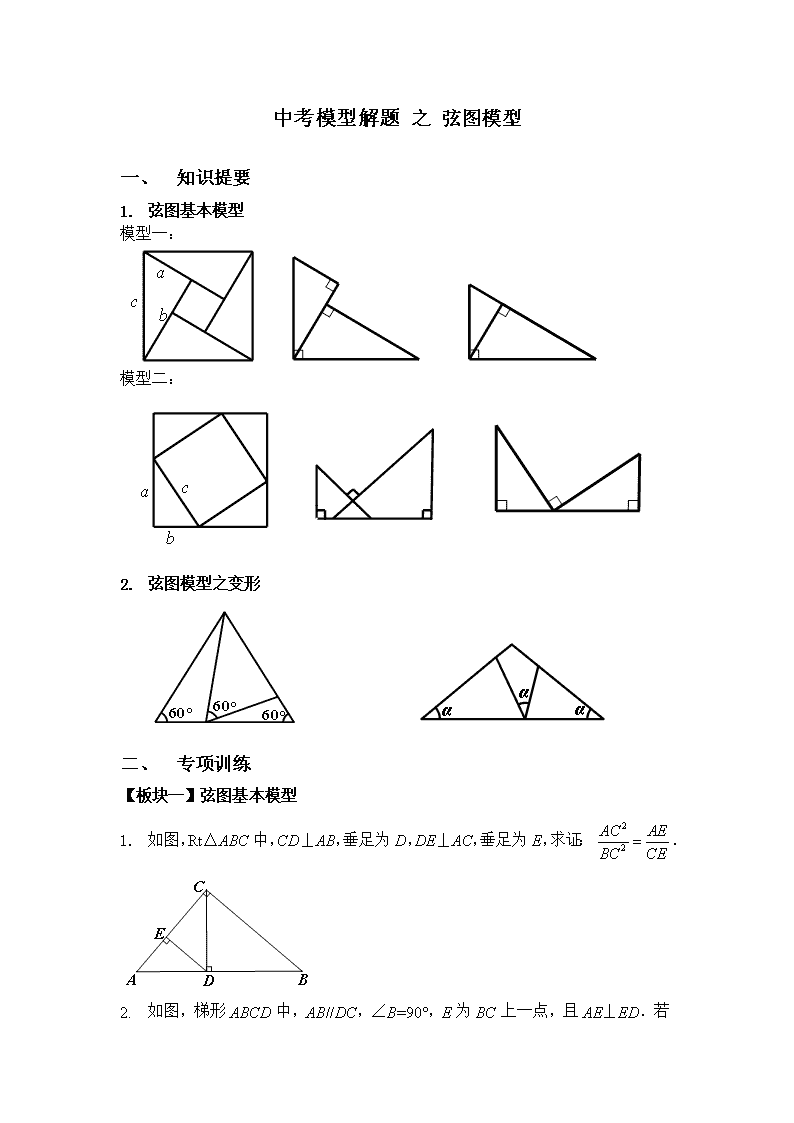
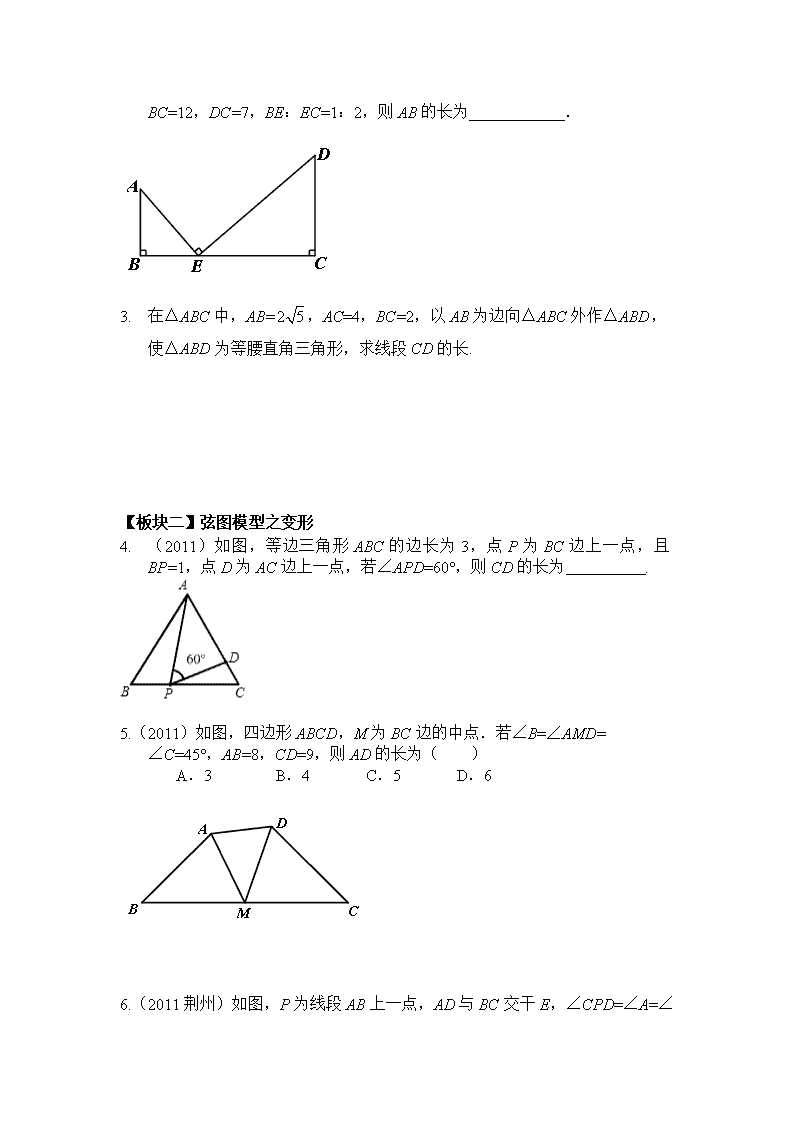
中考模型解题 之 弦图模型
中考模型解题 之 弦图模型 一、 知识提要 1. 弦图基本模型 模型一: 模型二: 2. 弦图模型之变形 二、 专项训练 【板块一】弦图基本模型 1. 如图,Rt△ABC中,CD⊥AB,垂足为D,DE⊥AC,垂足为E,求证:. 2. 如图,梯形ABCD中,AB//DC,∠B=90°,E为BC上一点,且AE⊥ED.若BC= 12,DC=7,BE:EC=1:2,则AB的长为____________. 1. 在△ABC中,AB=,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长. 【板块二】弦图模型之变形 2. (2011)如图,等边三角形ABC的边长为3,点P为BC边上一点,且BP=1,点D为AC边上一点,若∠APD=60°,则CD的长为 . 5.(2011)如图,四边形ABCD,M为BC边的中点.若∠B=∠AMD= ∠C=45°,AB=8,CD=9,则AD的长为( ) A.3 B.4 C.5 D.6 6.(2011荆州)如图,P为线段AB上一点,AD与BC交干E,∠CPD=∠A=∠ B,BC交PD于F,AD交PC于G,则图中相似三角形有( ) A.1对 B.2对 C.3对 D.4对 7. 在△ABC中,AC=BC,∠ACB=90°,点M是AC上的一点,点N是BC上的一点,沿着直线MN折叠,使得点C恰好落在边AB上的P点, 求证:MC:NC=AP:PB.查看更多