【数学】2018届一轮复习人教B版集合与常用逻辑用语学案
.第一章 集合与常用逻辑用语
考纲链接
1.集合
(1)集合的含义与表示
①了解集合的含义,体会元素与集合的属于关系.
②能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.
(2)集合间的基本关系
①理解集合之间包含与相等的含义,能识别给定集合的子集.
②在具体情境中,了解全集与空集的含义.
(3)集合的基本运算
①理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.
②理解在给定集合中一个子集的补集的含义,会求给定子集的补集.
③能使用Venn图表达集合间的基本关系及集合的基本运算.
2.常用逻辑用语
(1)理解命题的概念.
(2)了解“若p,则q”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系.
(3)理解必要条件、充分条件与充要条件的含义.
(4)了解逻辑联结词“或”“且”“非”的含义.
(5)理解全称量词和存在量词的意义.
(6)能正确地对含一个量词的命题进行否定.
1.1 集合及其运算
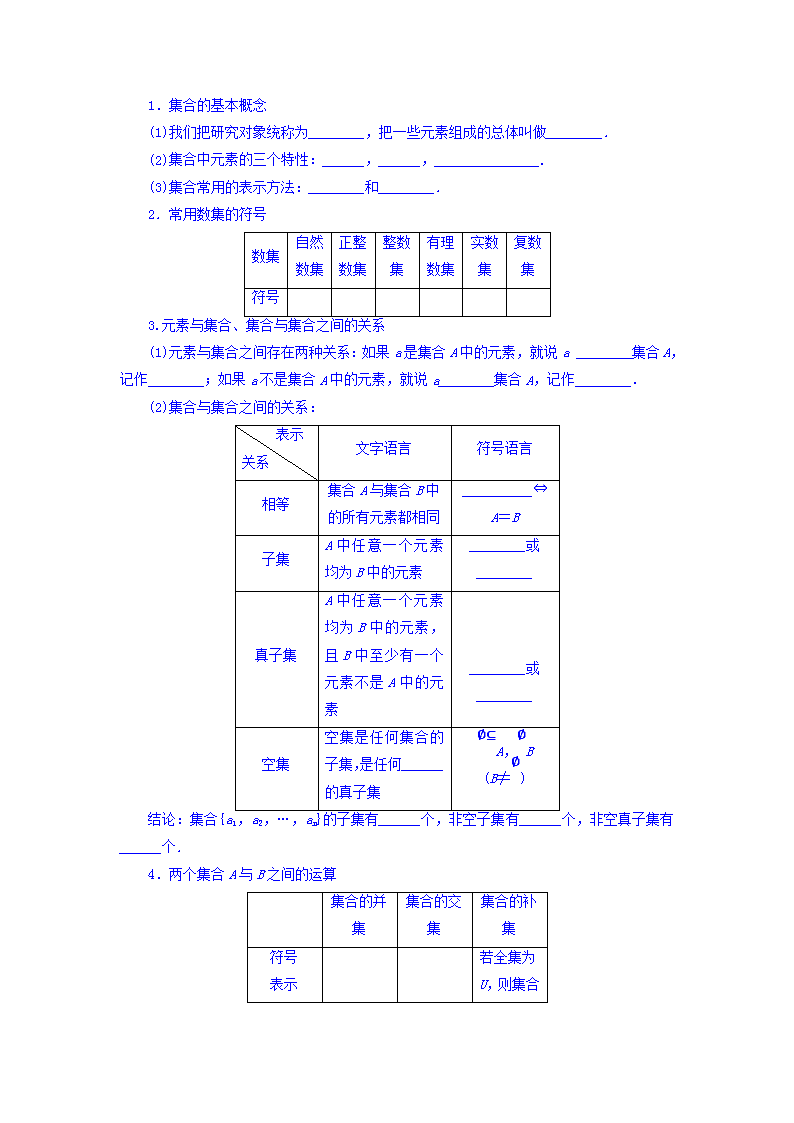
1.集合的基本概念
(1)我们把研究对象统称为________,把一些元素组成的总体叫做________.
(2)集合中元素的三个特性:______,______,_______________.
(3)集合常用的表示方法:________和________.
2.常用数集的符号
数集
自然数集
正整数集
整数集
有理数集
实数集
复数集
符号
3.元素与集合、集合与集合之间的关系
(1)元素与集合之间存在两种关系:如果a是集合A中的元素,就说a ________集合A,记作________;如果a不是集合A中的元素,就说a________集合A,记作________.
(2)集合与集合之间的关系:
表示
关系
文字语言
符号语言
相等
集合A与集合B中的所有元素都相同
__________⇔
A=B
子集
A中任意一个元素均为B中的元素
________或________
真子集
A中任意一个元素均为B中的元素,且B中至少有一个元素不是A中的元素
________或________
空集
空集是任何集合的子集,是任何______的真子集
∅⊆A,∅B
(B≠∅)
结论:集合{a1,a2,…,an}的子集有______个,非空子集有______个,非空真子集有______个.
4.两个集合A与B之间的运算
集合的并集
集合的交集
集合的补集
符号
表示
若全集为U,则集合
A的补集记为________
Venn图表示(阴影部分)
意义
5.集合运算中常用的结论
(1)①A∩B________A;②A∩B________B;
③A∩A=________; ④A∩∅=________;
⑤A∩B________B∩A.
(2)①A∪B________A; ②A∪B________B;
③A∪A=________; ④A∪∅=________;
⑤A∪B________B∪A.
(3)①∁U(∁UA)=________;②∁UU=________;
③∁U∅=________;
④A∩(∁UA)=____________;
⑤A∪(∁UA)=____________;
(4)①A∩B=A⇔________⇔A∪B=B;
②A∩B=A∪B⇔____________.
(5)记有限集合A,B的元素个数为card(A),card(B),则:
card(A∪B)=__________________________;
card=________________________.
自查自纠:
1.(1)元素 集合 (2)确定性 互异性 无序性 (3)列举法 描述法
2.N N*(N+) Z Q R C
3.(1)属于 a∈A 不属于 a∉A
(2)A⊆B且B⊆A A⊆B B⊇A AB BA
非空集合 2n 2n-1 2n-2
4.A∪B A∩B ∁UA {x|x∈A或x∈B}
{x|x∈A且x∈B} {x|x∈U且x∉A}
5.(1)①⊆ ②⊆ ③A ④∅ ⑤=
(2)①⊇ ②⊇ ③A ④A ⑤=
(3)①A ②∅ ③U ④∅ ⑤U
(4)①A⊆B ②A=B
(5)card(A)+card(B)-card(A∩B)
card(U)-card(A)-card(B)+card(A∩B)
()已知集合A={x||x|<2}, B={-1,0,1,2,3},则A∩B=( )
A.{0,1} B.{0,1,2}
C.{-1,0,1} D.{-1,0,1,2}
解:由A={x|-2<x<2},得A∩B={-1,0,1}.故选C.
()设集合M={x|x2=x},N={x|lgx≤0},则M∪N=( )
A. B.(0,1]
C.
解:因为M={x|x2=x}={0,1},N={x|lgx≤0}={x|0<x≤1},所以M∪N=.故选A.
()设集合A={y|y=2x,x∈R},B={x|x2-1<0},则A∪B=( )
A.(-1,1) B.(0,1)
C.(-1,+∞) D.(0,+∞)
解:易知A=(0,+∞),B={x|-1<x<1},所以A∪B=(-1,+∞).故选C.
设A={1,4,2x},B={1,x2},若B⊆A,则x的值为________.
解:当x2=4时,x=±2,若x=2,则不满足集合中的元素的互异性,所以x≠2;若x=-2,则A={1,4,-4},B={1,4},满足题意.当x2=2x时,x=0或2(舍去),x=0满足题意,所以x=0或-2.故填0或-2.
设集合A={x|x2+2x-3>0},集合B={x|x2-2ax-1≤0,a>0}.若A∩B中恰含有一个整数,则实数a的取值范围是________.
解:A={x|x2+2x-3>0}={x|x>1或x<-3},设函数f(x)=x2-2ax-1,则其对称轴x=a>0,由对称性知,若A∩B中恰含有一个整数,则这个整数为2,所以f(2)≤0且f(3)>0,即 得≤a<.故填.
类型一 集合的概念
(1)若集合A={x∈R|ax2+ax+1=0}中只有一个元素,则a=( )
A.4 B.2 C.0 D.0或4
解:由ax2+ax+1=0只有一个实数解,可得当a=0时,方程无实数解;
当a≠0时,Δ=a2-4a=0,解得a=4.故选A.
(2)已知集合A={m+2,2m2+m},若3∈A,则log2 018的值为________.
解:因为3∈A,所以m+2=3或2m2+m=3.
当m+2=3,即m=1时,2m2+m=3,不满足集合中元素的互异性,所以m=1不符合题意,舍去;
当2m2+m=3时,解得m=-或m=1(舍去).
此时当m=-时,m+2=≠3,符合题意.
所以m=-,log2 018=log2 0181=0.故填0.
点拨:
(1)用描述法表示集合,首先要弄清楚集合中代表元素的含义,再看元素的限制条件,明白集合的类型,是数集、点集还是其他类型集合.(2)含有字母的集合,在求出字母的值后,要注意检验集合中的元素是否满足互异性.
(1)()集合 中含有的元素个数为( )
A.4 B.6 C.8 D.12
解:令x=1,2,3,4,5,6,7,8,9,10,11,12,代入验证,得x=1,2,3,4,6,12时,∈Z,即集合中有6个元素.故选B.
(2)已知a∈R,b∈R,若={a2,a+b,0},则a2 017+b2 017=________.
解:由已知得=0及a≠0,所以b=0,于是a2=1,即a=1或a=-1,又根据集合中元素的互异性可知a=-1,所以a2 017+b2 017=-1.故填-1.
类型二 集合间的关系
已知集合A={x|x2-3x-10≤0}.
(1)若B={x|m+1≤x≤2m-1},B⊆A,求实数m的取值范围;
(2)若B={x|m-6≤x≤2m-1},A=B,求实数m的取值范围;
(3)若B={x|m-6≤x≤2m-1},A⊆B,求实数m的取值范围.
解:由A={x|x2-3x-10≤0},得A={x|-2≤x≤5},
(1)若B⊆A,则
①当B=∅,有m+1>2m-1,即m<2,此时满足B⊆A;
②当B≠∅,有 解得2≤m≤3.
由①②得,m的取值范围是(-∞,3].
(2)若A=B,则必有 解得m∈∅,即不存在实数m使得A=B.
(3)若A⊆B,则
解得3≤m≤4.所以m的取值范围为.
点拨:
本例主要考查了集合间的关系,“当B⊆A时,B可能为空集”很容易被忽视,要注意这一“陷阱”.
集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若B⊆A,求实数m的取值范围;
(2)当x∈Z时,求A的非空真子集的个数;
(3)当x∈R时,若A∩B=∅,求实数m的取值范围.
解:(1)①当m+1>2m-1,即m<2时,B=∅,满足B⊆A.
②当m+1≤2m-1,即m≥2时,要使B⊆A成立,则 可得2≤m≤3.
综上,m的取值范围是(-∞,3].
(2)当x∈Z时,A={-2,-1,0,1,2,3,4,5},
所以A的非空真子集个数为28-2=254.
(3)因为x∈R,且A∩B=∅,
所以当B=∅时,即m+1>2m-1,得m<2,满足条件;
当B≠∅时,有或 解得m>4.
综上,m的取值范围是(-∞,2)∪(4,+∞).
类型三 集合的运算
(1)已知全集U=R,集合A={x|lg x≤0},B={x|2x≤},则A∪B=( )
A.∅ B. C. D.(-∞,1]
解:由题意知,A=(0,1],B=,所以A∪B=(-∞,1].故选D.
(2)已知集合A,B均为全集U={1,2,3,4}的子集,且∁U(A∪B)={4},B={1,2},则A∩(∁UB)=________.
解:因为U={1,2,3,4},∁U(A∪B)={4},所以A∪B={1,2,3}.又因为B={1,2},所以{3}⊆A⊆{1,2,3}.又∁UB={3,4},所以A∩(∁UB)={3}.故填{3}.
(3)已知集合A={x∈R||x+2|<3},集合B={x∈R|(x-m)(x-2)<0},且A∩B=(-1,n),则m=________,n=________.
解:A={x∈R||x+2|<3}={x∈R|-5
1},则∁RM={x|x≤1},且N={x|-1≤x≤3},所以N∩(∁RM)=.故选C.
(2)()集合M={2,log3a},N={a,b},若M∩N={1},则M∪N=( )
A.{0,1,2} B.{0,1,3}
C.{0,2,3} D.{1,2,3}
解:因为M∩N={1},所以log3a=1,即a=3,所以b=1.所以M={2,1},N={3,1},M∪N={1,2,3}.故选D.
(3)设集合A={x||x-a|<1,x∈R},B={x|15-a,所以a>3;
当B={2}时, 解得a=3.
综上所述,所求a的取值范围是{a|a≥3}.
11.已知集合A={x∈R|ax2-3x+2=0,a∈R}.
(1)若A是空集,求a的取值范围;
(2)若A中只有一个元素,求a的值,并把这个元素写出来;
(3)若A中至多有一个元素,求a的取值范围.
解:(1)A是空集,即方程ax2-3x+2=0无解,
得 所以a>,
即实数a的取值范围是.
(2)当a=0时,A中只有一个元素;
当a≠0时,Δ=0,得a=,此时方程有两个相等的实数根,A中只有一个元素,
所以当a=0或a=时,A中只有一个元素,分别是和.
(3)A中至多有一个元素,包括A是空集和A中只有一个元素两种情况,根据(1),(2)的结果,得a=0或a≥,即a的取值范围是.
()设数列A:a1,a2,…,aN(N≥2).如果对小于n(2≤n≤N)的每个正整数k都有ak<an,则称n是数列A的一个“G时刻”.记G(A)是数列A的所有“G时刻”组成的集合.
(1)对数列A:-2,2,-1,1,3,写出G(A)的所有元素;
(2)证明:若数列A中存在an使得an>a1,则G(A)≠∅.
解:(1)G(A)的元素为2和5.
(2)证明:因为存在an使得an>a1,
所以{i∈N*|2≤i≤N,ai>a1}≠∅.
记m=min{i∈N*|2≤i≤N,ai>a1},
则m≥2,且对任意正整数k<m,ak≤a1<am.
因此m∈G(A),从而G(A)≠∅.
1.2 命题及其关系、充分条件与必要条件
1.命题的概念
(1)一般地,在数学中,我们把用语言、符号或式子表达的,可以__________的陈述句叫做命题,其中__________的语句叫做真命题,____________的语句叫做假命题.
(2)在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,我们称这两个命题为____________.
(3)在两个命题中,如果一个命题的条件和结论恰好是另一个命题的条件的否定和结论的否定,这样的两个命题称为________________.
(4)在两个命题中,如果一个命题的条件和结论恰好是另一个命题的结论的否定和条件的否定,这样的两个命题称为________________.
(5)一般地,设“若p,则q”为原命题,那么______________就叫做原命题的逆命题;________________就叫做原命题的否命题;________________就叫做原命题的逆否命题.
2.四种命题间的相互关系
(1)四种命题间的相互关系图(请你补全)
(2)真假关系
①两个命题互为逆否命题,它们具有________的真假性,即等价;
②两个命题为互逆命题或互否命题,它们的真假性________.
3.充分条件和必要条件
(1)如果p⇒q,则称p是q的______,q是p的_________________________________________.
(2)如果________,且________,那么称p是q的充分必要条件,简称p是q的__________,记作________.
(3)如果p⇒q,但qp,那么称p是q的________条件.
(4)如果________,但________,那么称p是q的必要不充分条件.
(5)如果________,且________,那么称p是q的既不充分也不必要条件.
自查自纠
1.(1)判断真假 判断为真 判断为假
(2)互逆命题 (3)互否命题 (4)互为逆否命题
(5)若q,则p 若綈p,则綈q 若綈q,则綈p
2.(1)
(2)①相同 ②没有关系
3.(1)充分条件 必要条件
(2)p⇒q q⇒p 充要条件 p⇔q
(3)充分不必要
(4)pq q⇒p (5)pq qp
下列语句为命题的是( )
A.对角线相等的四边形
B.a<5
C.x2-x+1=0
D.有一个内角是90°的三角形是直角三角形
解:只有选项D是可以判断真假的陈述句,故选D.
下列命题中是真命题的是( )
A.若向量a,b满足a·b=0,则a=0或b=0
B.若ab>0,则logab>0时,因为y=logx为减函数,所以logab不成立,故逆命题为假命题,从而否命题为假命题.故选C.
命题“若x,y都是偶数,则x+y也是偶数”的逆否命题是____________________.
解:“都是”的否定是“不都是”,故其逆否命题是“若x+y不是偶数,则x,y不都是偶数”.故填若x+y不是偶数,则x,y不都是偶数.
“m<”是“一元二次方程x2+x+m=0有实数解”的________条件.(选填“充分不必要”“必要不充分”“充要”“既不充分也不必要”)
解:因为x2+x+m=0有实数解等价于Δ=1-4m≥0,得m≤,所以“m<”是“一元二次方程x2+x+m=0有实数解”的充分不必要条件.故填充分不必要.
类型一 四种命题及其相互关系
写出下列命题的逆命题、否命题及逆否命题,并分别判断四种命题的真假:
(1)末位数字是0的多位数一定是5的倍数;
(2)在△ABC中,若AB>AC,则∠C>∠B;
(3)若x2-2x-3>0,则x<-1或x>3.
解:(1)原命题:若一个多位数的末位数字是0,则它是5的倍数.
逆命题:若一个多位数是5的倍数,则它的末位数字是0.
否命题:若一个多位数的末位数字不是0,则它不是5的倍数.
逆否命题:若一个多位数不是5的倍数,则它的末位数字不是0.
这里,原命题与逆否命题为真命题,逆命题与否命题是假命题.
(2)逆命题:在△ABC中,若∠C>∠B,则AB>AC.
否命题:在△ABC中,若AB≤AC,则∠C≤∠B.
逆否命题:在△ABC中,若∠C≤∠B,则AB≤AC.
这里,四种命题都是真命题.
(3)逆命题:若x<-1或x>3,则x2-2x-3>0.
否命题:若x2-2x-3≤0,则-1≤x≤3.
逆否命题:若-1≤x≤3,则x2-2x-3≤0.
这里,四种命题都是真命题.
点拨:
写出一个命题的逆命题、否命题和逆否命题,关键是找出原命题的条件p与结论q,将原命题写成“若p,则q”的形式.在(2)中,原命题有大前提“在△ABC中”,在写出它的逆命题、否命题和逆否命题时,应当保留这个大前提.(3)中“x<-1或x>3”的否定形式是“x≥-1且x≤3”,即“-1≤x≤3”.
写出下列命题的否定形式和否命题:
(1)若xy=0,则x,y中至少有一个为零;
(2)若a+b=0,则a,b中最多有一个大于零;
(3)若四边形是平行四边形,则其相邻两个内角相等;
(4)有理数都能写成分数.
解:(1)否定形式:若xy=0,则x,y都不为零.
否命题:若xy≠0,则x,y都不为零.
(2)否定形式:若a+b=0,则a,b都大于零.
否命题:若a+b≠0,则a,b都大于零.
(3)否定形式:若四边形是平行四边形,则它的相邻内角不都相等.
否命题:若四边形不是平行四边形,则它的相邻内角不都相等.
(4)否定形式:有理数不都能写成分数.
否命题:非有理数不都能写成分数.
类型二 充要条件的判定
指出下列命题中,p是q的什么条件(在“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选出一种作答).
(1)在△ABC中,p:A=B,q:sinA=sinB;
(2)已知x,y∈R,p:(x-1)2+(y-2)2=0,q:(x-1)(y-2)=0;
(3)非空集合A,B中,p:x∈(A∪B),q:x∈B;
(4)对于实数x,y,p:x+y≠8,q:x≠2或y≠6.
解:(1)在△ABC中,A=B⇒sinA=sinB;反之,若sinA=sinB,因为A与B不可能互补(三角形三个内角之和为180°),所以只有A=B,故p是q的充要条件.
(2)条件p:x=1且y=2,条件q:x=1或y=2,所以p⇒q但qp,故p是q的充分不必要条件.
(3)显然x∈(A∪B)不一定有x∈B,但x∈B一定有x∈(A∪B),所以p是q的必要不充分条件.
(4)易知綈p:x+y=8,綈q:x=2且y=6,显然綈q⇒綈p,但綈p綈q,即綈q是綈p的充分不必要条件,根据原命题和逆否命题的等价性知,p是q的充分不必要条件.
点拨:
充要条件的三种判断方法:
(1)定义法:根据p⇒q,q⇒p进行判断;
(2)集合法:根据p,q成立的对象的集合之间的包含关系进行判断;
(3)等价转化法:根据一个命题与其逆否命题的等价性,把要判断的命题转化为其逆否命题进行判断.这个方法特别适合以否定形式给出的问题,如“xy≠1”是“x≠1或y≠1”的某种条件,即可转化为判断“x=1且y=1”是“xy=1”的某种条件.
(1)“sinα=”是“cos2α=”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
解法一:(定义法)
若sinα=,则cos2α=1-2sin2α=1-2×=,充分性成立;反之,若cos2α=,则有1-2sin2α=,得sin2α=,sinα=±,必要性不成立.
因此,“sinα=”是“cos2α=”的充分不必要条件.
解法二:(集合法)
令A={α|p(α)},B={α|q(α)},
则可得A=,
B==
=.
显然,AB,所以p是q的充分不必要条件.故选A.
(2)给定两个命题p,q,若綈p是q的必要而不充分条件,则p是綈q的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
解:因为綈p是q的必要而不充分条件,所以綈q是p的必要而不充分条件,从而得出p是綈q的充分而不必要条件.故选A.
类型三 充要条件的证明与探求
“数列{an}的前n项和Sn=An2+Bn(A,B是常数)”是“数列{an}是等差数列”的什么条件?
解:当n>1时,an=Sn-Sn-1=2An+B-A;
当n=1时,a1=S1=A+B,适合an=2An+B-A.
所以an=2An+B-A,显然{an}是等差数列,故充分性成立.
反之,若{an}是等差数列,则有Sn=na1+d(d为公差),即Sn=n2+n.
设A=,B=a1-,即得Sn=An2+Bn,
因此,必要性成立.
所以“Sn=An2+Bn(A,B是常数)”是“数列{an}是等差数列”的充要条件.
点拨:
在证明与探求充要条件时,容易出现如下错误:①张冠李戴,证明过程中把充分性与必要性搞反了;②证明充分性或必要性时,没有把p(或q)作为条件推出q(或p).
已知m∈Z,关于x的一元二次方程
x2-4x+4m=0,①
x2-4mx+4m2-4m-5=0,②
求方程①②的根都是整数的充要条件.
解:方程①有实数根⇔Δ=16-16m≥0,即m≤1,
方程②有实数根⇔Δ=16m+20≥0,即m≥-,
所以方程①②都有实数根⇔-≤m≤1.
因为m∈Z,所以m=-1,0,1.
当m=-1时,方程①可化为x2-4x-4=0,无整数解;
当m=0时,方程②可化为x2-5=0,无整数解;
当m=1时,方程①②都有整数解.
综上所述,方程①②的根都是整数的充要条件是m=1.
类型四 充要条件的应用
(1)设p:|4x-3|≤1,q:x2-(2a+1)x+a(a+1)≤0,若綈p是綈q的必要不充分条件,则实数a的取值范围是( )
A.
B.
C.(-∞,0]∪
D.(-∞,0)∪
解:由|4x-3|≤1得≤x≤1,由x2-(2a+1)x+a(a+1)=(x-a)≤0得a≤x≤a+1,
因为綈p是綈q的必要不充分条件,
所以p是q的充分不必要条件,有 或 得0≤a≤.故选A.
(2)已知命题p:x2+2x-3>0;命题q:x>a,且綈q的一个充分不必要条件是綈p,则a的取值范围是( )
A.
C.
解:由x2+2x-3>0,得x<-3或x>1,由綈q的一个充分不必要条件是綈p,可知綈p是綈q的充分不必要条件,等价于q是p的充分不必要条件,有a≥1.故选A.
点拨:
解决此类问题一般是把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(组)求解,在求解参数的取值范围时,一定要注意对区间端点值的检验,尤其是利用两个集合之间的关系求解参数的取值范围时,不等式是否能够取等号决定端点值的取舍,处理不当容易出现漏解或增解的情形.
(1)()函数f(x)= 有且只有一个零点的充分不必要条件是( )
A.a<0 B.01
解:因为函数f(x)过点(1,0),所以函数f(x)有且只有一个零点⇔函数y=-2x+a(x≤0)没有零点⇔函数y=2x(x≤0)与直线y=a无公共点.数形结合可得a≤0或a>1.观察选项,根据集合间关系{a|a<0}{a|a≤0或a>1},知A正确.故选A.
(2)若“xm+1”是“x2-2x-3>0”的必要不充分条件,则实数m的取值范围是________.
解:由已知易得{x|x2-2x-3>0}{x|xm+1},又{x|x2-2x-3>0}={x|x<-1或x>3},所以或 解得0≤m≤2.故填.
1.命题及判断命题的真假
(1)判断一个语句是否为命题,就是要看它是否具备“是陈述句”和“可以判断真假”这两个条件.只有这两个条件都具备的语句才是命题.
(2)判断一个命题的真假,首先要分清命题的条件和结论.对涉及数学概念的命题真假的判断,要以数学定义、定理为依据(数学定义、定理都是命题,且都是真命题),从概念的本身入手进行判断.
2.四种命题间的相互关系及应用
(1)在判断四种命题之间的关系时,首先要注意分清命题的条件与结论,再比较每个命题的条件与结论之间的关系.要注意四种命题关系的相对性,一旦一个命题定为原命题,也就相应地有了它的“逆命题”“否命题”“逆否命题”.
(2)当一个命题有大前提而要写其他三种命题时,必须保留大前提,也就是大前提不动;对于由多个并列条件组成的命题,在写其他三种命题时,应把其中一个(或几个)作为大前提.
(3)判断命题的真假,如果不易直接判断,可正难则反,应用互为逆否命题的等价性来判断.
3.“否命题”与“命题的否定”的区别.“否命题”与“命题的否定”是两个不同的概念,“否命题”是对原命题既否定其条件,又否定其结论,而“命题的否定”只否定命题的结论.
4.充要条件的三种判断方法
(1)定义法:分三步进行,第一步,分清条件与结论;第二步,判断p⇒q及q⇒p的真假;第三步,下结论.
(2)等价法:将命题转化为另一个等价且容易判断真假的命题.一般地,这类问题由几个充分必要条件混杂在一起,可以画出关系图,运用逻辑推理判断真假.
(3)集合法:写出集合A={x|p(x)}及B={x|q(x)},利用集合之间的包含关系加以判断:
①若A⊆B,则p是q的充分条件;
②若AB,则p是q的充分不必要条件;
③若B⊆A,则p是q的必要条件;
④若BA,则p是q的必要不充分条件;
⑤若A=B,则p是q的充要条件;
⑥若AB且BA,则p是q的既不充分也不必要条件.
1.设a,b是向量,命题“若a=-b,则|a|=|b|”的逆命题是( )
A.若a≠-b,则|a|≠|b|
B.若a=-b,则|a|≠|b|
C.若|a|≠|b|,则a≠-b
D.若|a|=|b|,则a=-b
解:只需将原命题的结论变成新命题的条件,同时将原命题的条件变成新命题的结论即可,即“若|a|=|b|,则a=-b”.故选D.
2.与命题“若a∈M,则b∉M”等价的命题是( )
A.若a∉M,则b∉M
B.若b∉M,则a∈M
C.若b∈M,则a∉M
D.若a∉M,则b∈M
解:命题“若a∈M,则b∉M”的逆否命题是“若b∈M,则a∉M”,又原命题与逆否命题互为等价命题,故选C.
3.()设p:11,则p是q成立的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
解:由q:2x>1,解得x>0,易知,p能推出q,但q不能推出p,故p是q成立的充分不必要条件.故选A.
4.下列有关命题的说法正确的是( )
A.命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”
B.“x=-1”是“x2-5x-6=0”的必要不充分条件
C.命题“∃x∈R,使得x2+x+1<0”的否定是“∀x∈R,均有x2+x+1<0”
D.命题“若x=y,则cosx=cosy”的逆否命题为真命题
解:A中,否命题应为“若x2≠1,则x≠1”;B中,x=-1⇒x2-5x-6=0,
反之则不成立,应为充分不必要条件;C中,命题的否定应为“∀x∈R,均有x2+x+1≥0”;D中,原命题为真命题,因此,其逆否命题为真命题.故选D.
5.()设U为全集,A,B是集合,则“存在集合C使得A⊆C,B⊆∁UC”是“A∩B=∅”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
解:若存在集合C,使得A⊆C,B⊆∁UC,则A∩B⊆C∩(∁UC)=∅;反过来,若A∩B=∅,由Venn图可知,一定存在集合C使得A⊆C,B⊆∁UC.故选C.
6.()下列选项中,p是q的必要不充分条件的是( )
A.p:x=1,q:x2=x
B.p:|a|>|b|,q:a2>b2
C.p:x>a2+b2,q:x>2ab
D.p:a+c>b+d,q:a>b且c>d
解:A中,x=1⇒x2=x,x2=x⇒x=0或x=1x=1,故p是q的充分不必要条件;B中,|a|>|b|,根据不等式的性质可得a2>b2,反之也成立,故p是q的充要条件;C中,因为a2+b2≥2ab,所以由x>a2+b2,得x>2ab,反之不成立,故p是q的充分不必要条件;D中,取a=-1,b=1,c=0,d=-3,满足a+c>b+d,但a<b,c>d;反之,由同向不等式可加性知a>b,c>d⇒a+c>b+d,故p是q的必要不充分条件.故选D.
7.设n∈N+,一元二次方程x2-4x+n=0有整数根的充要条件是n=__________.
解:x==2±,因为x是整数,即2±为整数,所以为整数,且n≤4.又因为n∈N+,所以可取n=1,2,3,4,验证可知n=3,4符合题意;反之,当n=3,4时,可推出一元二次方程x2-4x+n=0有整数根.故填3或4.
8.方程+=1表示曲线C,给出以下命题:
①曲线C不可能为圆;
②若14;
④若曲线C为焦点在x轴上的椭圆,则14时,方程表示双曲线;当4-t>t-1>0时,方程表示焦点在x轴上的椭圆,解得1<t<.故填③④.
9.写出命题“若+(y+1)2=0,则x=2且y=-1”的逆命题、否命题、逆否命题,并判断它们的真假.
解:逆命题:若x=2且y=-1,则+(y+1)2=0;(真)
否命题:若+(y+1)2≠0,则x≠2或y≠-1;(真)
逆否命题:若x≠2或y≠-1,则+(y+1)2≠0.(真).
10.已知P={x|x2-8x-20≤0},S={x|1-m≤x≤1+m}.
(1)是否存在实数m,使“x∈P”是“x∈S”的充要条件,若存在,求出m的取值范围;
(2)是否存在实数m,使“x∈P”是“x∈S”的必要条件,若存在,求出m的取值范围.
解:由x2-8x-20≤0,得-2≤x≤10,
所以P={x|-2≤x≤10}.
(1)因为“x∈P”是“x∈S”的充要条件,所以P=S,
有 得 这样的m不存在.
(2)因为“x∈P”是“x∈S”的必要条件,所以S⊆P,
有 得m≤3,即m的取值范围是(-∞,3].
11.已知p:≤2,q:x2-2x+1-m2≤0(m>0),若綈p是綈q的必要不充分条件,求实数m的取值范围.
解:由≤2得-2≤x≤10,
由x2-2x+1-m2=≤0(m>0)
得1-m≤x≤1+m.
因为綈p是綈q的必要不充分条件,
所以p是q的充分不必要条件,
所以{x|-2≤x≤10}⊆{x|1-m≤x≤1+m},
有或 得m≥9.
所以实数m的取值范围是2-4×4×1<0,解得10恒成立;命题q:函数f(x)=log(x2-2ax+3a)是区间时,不等式x2+ax-2>0恒成立,
所以a>=-x在x∈时恒成立,
令g(x)=-x,则g(x)在上是减函数,
所以g(x)max=g(1)=1,
所以a>1.即若命题p真,则a>1.
又因为函数f(x)=log(x2-2ax+3a)是区间,x2-lnx-a≥0与命题q:∃x0∈R,x+2ax0-8-6a=0都是真命题,则实数a的取值范围是________.
解:若p真,则∀x∈,a≤,
令f(x)=x2-lnx,则f′(x)=x-≥0在上恒成立,所以f(x)min=f(1)=,所以a≤;
若q真,则(2a)2-4×1×(-8-6a)=4(a+2)(a+4)≥0,
得a≤-4或a≥-2.
所以实数a的取值范围为(-∞, -4]∪.故填(-∞,-4]∪.
1.含有逻辑联结词命题真假的判断
判断一个含有逻辑联结词命题的真假,应先对该命题进行分解,判断出构成它的简单命题的真假,再根据真值表进行判断.
2.全称命题与特称命题真假的判断
(1)要判断全称命题是真命题,需要对集合M中每个元素x,证明p(x)成立;如果在集合M中找到一个元素x0,使得p(x0)不成立,那么这个全称命题就是假命题.
(2)要判定一个特称命题是真命题,只要在限定的集合M中,至少能找一个x=x0,使
p(x0)成立即可;否则,这一特称命题就是假命题.
3.在有些命题中,逻辑联结词“或”“且”“非”是以另一种形式出现的.如“x=±1”中含逻辑联结词“或”,“≥”表示“大于或等于”;“綊”表示“平行且等于”,“并且”的含义为“且”;“∉”表示“不属于”,“不是”的含义为“非”等.
4.一些常用的正面叙述的词语及它们的否定词语表:
正面词语
等于(=)
大于(>)
小于(<)
是
都是
否定词语
不等于
(≠)
不大于
(≤)
不小于
(≥)
不是
不都是
正面
词语
至多有一个
至少有一个
任意的
所有的
一定
否定
词语
至少有两个
一个也没有
某个
某些
不一定
1.“a和b都不是偶数”的否定形式是( )
A.a和b至少有一个是偶数
B.a和b至多有一个是偶数
C.a是偶数,b不是偶数
D.a和b都是偶数
解:“a和b都不是偶数”的否定形式是“a和b至少有一个是偶数”.故选A.
2.()已知命题p:∀x>0,总有(x+1)ex>1,则綈p为( )
A.∃x0≤0,使得(x0+1)ex0≤1
B.∃x0>0,使得(x0+1)ex0≤1
C.∀x>0,总有(x+1)ex≤1
D.∀x≤0,总有(x+1)ex≤1
解:全称命题的否定是特称命题.故选B.
3.已知a>0,函数f(x)=ax2+bx+c,若x0满足关于x的方程2ax+b=0,则下列选项的命题中为假命题的是( )
A.∃x∈R,f(x)≤f(x0) B.∃x∈R,f(x)≥f(x0)
C.∀x∈R,f(x)≤f(x0) D.∀x∈R,f(x)≥f(x0)
解:因为函数f(x)的最小值是f=f(x0),所以∀x∈R,f(x)≥f(x0),选项C错误.故选C.
4.()已知命题p:存在x∈R,x2+1<2x;命题q:若mx2-mx-1<0恒成立,则-41,则ax>logax恒成立;命题q:在等差数列{an}中,“m+n=p+q”是“am+an=ap+aq(m,n,p,q∈N*)”的充分不必要条件,则下列选项中真命题是( )
A.(綈p)∧(綈q) B.(綈p)∨(綈q)
C.p∨(綈q) D.p∧q
解:当a=1.1,x=2时,
ax=1.12=1.21,logax=log1.12>log1.11.21=2,
此时,ax0,则命题“p∧(綈q)”是假命题;
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是=-3;
③命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”.
其中正确结论的序号为________.
解:①中命题p为真命题,命题q为真命题,所以p∧(綈q)为假命题,①正确;
②当a=b=0时,有l1⊥l2,②不正确;
易知③正确.所以正确结论的序号为①③.故填①③.
9.指出下列命题中,哪些是全称命题,哪些是特称命题,写出它们的否定形式,并判断否定形式的真假.
(1)若a>0且a≠1,则对任意实数x,ax>0;
(2)对任意实数x1,x2,若x1<x2,则tanx1<tanx2;
(3)∃T0∈R,使|sin(x+T0)|=|sinx|;
(4)∃x0∈R,使x+1<0.
解:(1)全称命题,其否定形式为:若a>0且a≠1,则∃x∈R,ax≤0,显然该命题为假命题.
(2)全称命题,其否定形式为:∃x1,x2∈R,且x1<x2,使tanx1≥tanx2,该命题为真命题.例如取x1=0,x2=π,有x1<x2,但tanx1=tanx2=0;又当x1=0,x2=时,有x1<x2,但tan0=0,tan= -,所以tanx1>tanx2.
(3)特称命题,其否定形式为:∀T∈R,|sin(x+T)|≠|sinx|,该命题是假命题.例如T0=π时,有|sin(x+π)|=|sinx|.
(4)特称命题,其否定形式为∀x∈R,x2+1≥0.因为x∈R时,x2≥0,所以x2+1≥1>0,故为真命题.
10.设命题p:实数x满足x2-4ax+3a2<0,其中a>0,命题q:实数x满足
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若綈p是綈q的充分不必要条件,求实数a的取值范围.
解:(1)由x2-4ax+3a2<0,得(x-3a)(x-a)<0,
因为a>0,所以ax+1
C.∀x>0,5x>3x
D.∃x0∈(0,+∞),x00),则f′(x)=1-cosx≥0恒成立,所以f(x)在(0,+∞)上单调递增,于是f(x)>f(0)=0恒成立.故选D.
8.设a,b为正数,则“a-b>1”是“a2-b2>1”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
解:a-b>1,即a>b+1.因为a,b为正数,所以a2>(b+1)2=b2+1+2b>b2+1,即a2-b2>1成立.反之,当a=,b=1时,满足a2-b2>1,但a-b>1不成立.所以“a-b>1”是“a2-b2>1”的充分不必要条件.故选A.
9.设命题p:∃x0∈(0,+∞),3x0+x0=2 018,命题q:∃a0∈(0,+∞),f(x)=|x|-a0x为偶函数,那么下列命题为真命题的是( )
A.p∧q B.(綈p)∧q
C.p∧(綈q) D.(綈p)∧(綈q)
解:p真q假,所以p∧(綈q)为真命题.故选C.
10.设函数f(x)=,集合M={x|f(x)<0},P={x|f′(x)>0},若M是P的真子集,则实数a的取值范围是( )
A.(-∞,1) B.(0,1)
C.(1,+∞) D.,依据定义得A⊕B={x|0≤x≤1或x>2}.故填{x|0≤x≤1或x>2}.
16.已知p:(x-m+1)(x-m-1)<0;q:<x<,若p是q的必要不充分条件,则实数m的取值范围是________________________.
解:因为p是q的必要不充分条件,所以{x|m-1<x<m+1},即 解得-<m<.当m=-时,,符合题意;当m=时,,符合题意.综上,-≤m≤.故填.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.(10分)写出下列命题的否定,并判断其真假:
(1)p:∀m∈R,方程x2+x-m=0必有实数根;
(2)q:∃x∈R,使得x2+x+1≤0.
解:(1)綈p:∃m∈R,使方程x2+x-m=0无实数根.
若方程x2+x-m=0无实数根,则Δ=1+4m<0,
解得m<-,
所以当m=-1时,綈p为真.
(2)綈q:∀x∈R,使得x2+x+1>0.
因为x2+x+1=+>0,
所以綈q为真.
18.(12分)已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R}.
(1)若A∩B=,求实数m的值;
(2)若A⊆∁RB,求实数m的取值范围.
解:A={x|-1≤x≤3},B={x|m-2≤x≤m+2}.
(1)因为A∩B=,所以 得m=3.
(2)∁RB={x|x<m-2,或x>m+2},
因为A⊆∁RB,所以m-2>3或m+2<-1,
解得m>5或m<-3.
所以实数m的取值范围是(-∞,-3)∪(5,+∞).
19.(12分)在平面直角坐标系xOy中,直线l与抛物线y2=2x相交于A,B两点.
(1)求证:“如果直线l过点T(3,0),那么·=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
解:(1)证明:设过点T(3,0)的直线l交抛物线y2=2x于点A(x1,y1),B(x2,y2).
当直线l的斜率不存在时,直线l的方程为x=3,此时,直线l与抛物线相交于点A(3,),B(3,-).
所以·=3.
当直线l的斜率存在时,设直线l的方程为y=k(x-3),其中k≠0.
由 得ky2-2y-6k=0,则y1y2=-6.
又因为x1=y,x2=y,
所以·=x1x2+y1y2=(y1y2)2+y1y2=3.
综上所述,命题“如果直线l过点T(3,0),那么·=3”是真命题.
(2)逆命题:在平面直角坐标系xOy中,直线l与抛物线y2=2x相交于A,B两点,如果·=3,那么直线l过点T(3,0).该命题是假命题.
例如:取抛物线上的点A(2,2),B,此时·=3,
直线AB的方程为2x-3y+2=0,而T(3,0)不在直线AB上.
20.(12分)已知命题“∀x∈,都有不等式x2-x-m<0成立”是真命题.
(1)求实数m的取值集合B;
(2)设不等式(x-3a)(x-a-2)<0的解集为A,若“x∈A”是“x∈B”的充分不必要条件,求实数a的取值范围.
解:(1)根据题意,不等式x2-x-m<0在-1≤x≤1时恒成立,所以m>(x2-x)max,得m>2,即集合B=(2,+∞).
(2)对于不等式(x-3a)(x-a-2)<0,
①当3a>a+2,即a>1时,解集A=(a+2,3a),若“x∈A”是“x∈B
”的充分不必要条件,即A⊆B成立,则a+2≥2,此时a∈(1,+∞);
②当3a=a+2,即a=1时,解集A=∅,若“x∈A”是“x∈B”的充分不必要条件,则A⊆B成立,此时a=1;
③当3a
查看更多