2017-2018学年上海市浦东新区高二上学期期末考试数学试题 解析版

2017-2018学年上海市浦东新区高二上学期期末考试数学试题 解析版

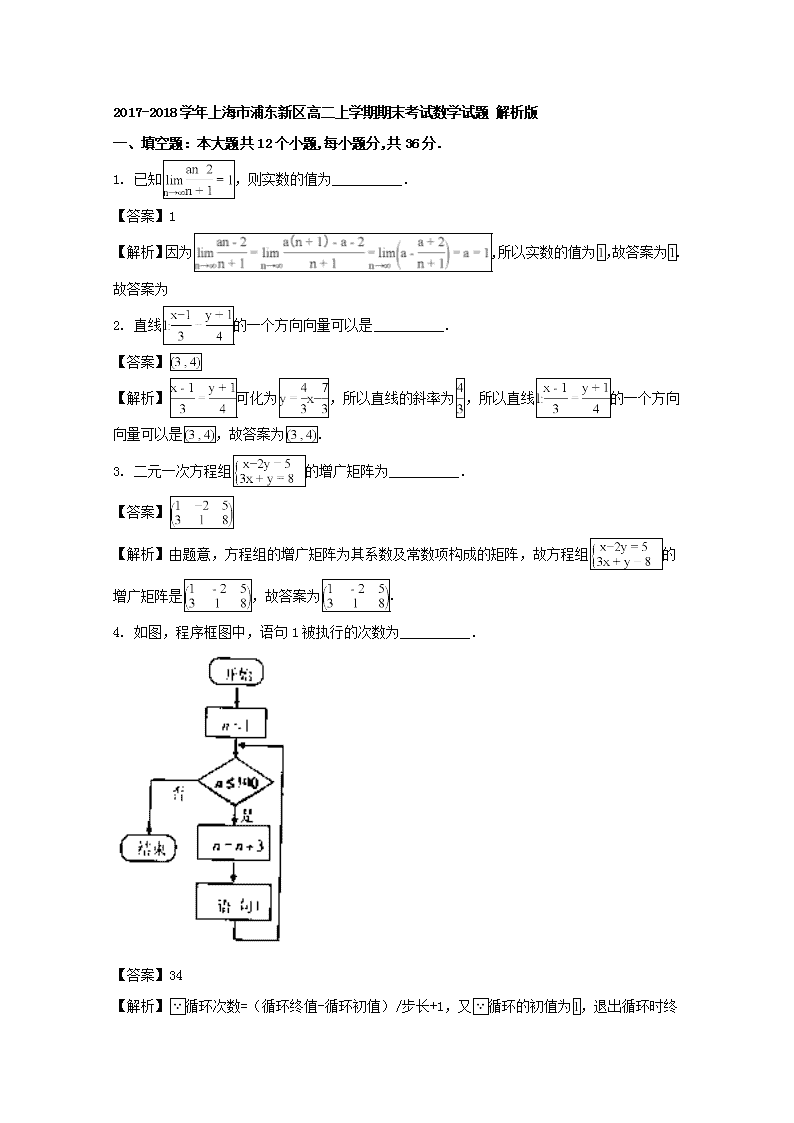
‎2017-2018学年上海市浦东新区高二上学期期末考试数学试题 解析版 一、填空题：本大题共12个小题,每小题分,共36分.‎ ‎1. 已知，则实数的值为__________．‎ ‎【答案】1‎ ‎【解析】因为,所以实数的值为，故答案为.‎ 故答案为 ‎2. 直线的一个方向向量可以是__________．‎ ‎【答案】‎ ‎【解析】可化为 ，所以直线的斜率为 ，所以直线的一个方向向量可以是，故答案为.‎ ‎3. 二元一次方程组的增广矩阵为__________．‎ ‎【答案】‎ ‎【解析】由题意，方程组的增广矩阵为其系数及常数项构成的矩阵，故方程组的增广矩阵是，故答案为.‎ ‎4. 如图，程序框图中，语句1被执行的次数为__________．‎ ‎【答案】34‎ ‎【解析】循环次数=（循环终值-循环初值）/步长+1，又循环的初值为，‎ 退出循环时终值为，步长为，故循环次数次，故答案为.‎ ‎5. 设数列的前项和为，若，则__________．‎ ‎【答案】15‎ ‎【解析】数列的前项和为，若，，故答案为.‎ ‎6. 设向量与的夹角为，，，则__________．‎ ‎【答案】‎ ‎【解析】，，，故答案为.‎ ‎7. 用数学归纳法证明：，当时，左边为__________．‎ ‎【答案】‎ ‎【解析】等式的左边是以为首项，为公比的等比数列的前项的和，观察当时，等式左边等于,故答案为.‎ ‎8. 已知等差数列中，，且，是数列的前项和，若取得最大值，则__________．‎ ‎【答案】8‎ ‎【解析】等差数列的公差， 时若取得最大值，故答案为.‎ ‎【方法点睛】本题主要考查等差数列的通项公式以及等差数列前项和的最值，属于难题. 求等差数列前项和的最大值的方法通常有两种：①将前项和表示成关于的二次函数， ，当时有最大值（若不是整数，等于离它较近的一个或两个整数时最大）；②可根据且确定最大时的值.本题根据方法①确定的取值范围的.‎ ‎9. 求和：__________．‎ ‎【答案】‎ ‎【解析】， ，故答案为.‎ ‎【方法点晴】本题主要考查等裂项相消法求数列的和，属于中档题. 裂项相消法是最难把握的求和方法之一，其原因是有时很难找到裂项的方向，突破这一难点的方法是根据式子的结构特点，常见的裂项技巧：(1)；（2） ； （3）；（4） ；此外，需注意裂项之后相消的过程中容易出现丢项或多项的问题，导致计算结果错误.‎ ‎10. 已知，，动点在轴上，当取最小值时，则点的坐标为__________．‎ ‎【答案】‎ ‎【解析】因为关于轴的对称点为，所以，当为直线与轴的交点时等号成立，即当为直线与轴的交点时取最小值，因为 ，所以直线的方程为 ，令 可得 ，所以 ，故答案为.‎ ‎11. 若关于的二元一次方程组有无穷多组解，则的取值为__________．‎ ‎【答案】2‎ ‎【解析】关于的二元一次方程组有无穷多组解，所以直线与直线重合，所以 ，解得 ，即的取值为，故答案为.‎ ‎12. 我们知道：，已知数列中，， ，则数列的通项公式__________．‎ ‎【答案】‎ ‎【解析】由，可得，所以 数列{为以为公比，以为首项的等比数列，所以，故答案为 ‎............‎ 二、选择题（每题3分，满分12分）‎ ‎13. 在平面上，四边形满足，，则四边形为（ ）‎ A. 梯形 B. 正方形 C. 菱形 D. 矩形 ‎【答案】C ‎【解析】，且四边形是平行四边形，，，四边形是菱形，故选C.‎ ‎14. 直线的倾斜角是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】，直线的斜率为，所以倾斜角是，故选A.‎ ‎15. 已知各项均为正数的等比数列中，，，则此数列的前项和等于（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】已知各项均为正数的等比数列中，，，设公比为，则由，得 ‎，故等比数列前项和为，故选B.‎ ‎16. 若动点到轴、轴的距离之比等于非零常数，则动点的轨迹方程是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】设，动点到轴、轴的距离之比等于非零常数，，即，故选D.‎ 三、解答题 （本大题共5小题，共52分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17. 已知直线与圆相交于两点.‎ ‎（1）求弦的长；‎ ‎（2）求弦的垂直平分线的方程.‎ ‎【答案】（1）2（2）‎ ‎【解析】试题分析：（1）把圆的方程化为标准形式，求得圆心和半径，再根据再根据点到直线距离公式及勾股定理可求得弦的长；（2）线段的垂直平分线经过圆心，且和直线垂直，用点斜式求得弦的垂直平分线的方程.‎ 试题解析：（1）因为圆心到直线的距离， ‎ 所以弦长. ‎ ‎（2）弦的垂直平分线的方程可设为， ‎ 由圆的性质知，弦的垂直平分线经过圆心，所以，， ‎ 所以，弦的垂直平分线的方程为.‎ ‎18. 已知，，，且.‎ ‎（1）求向量在向量的方向上的投影；‎ ‎（2）求实数的值及向量的坐标.‎ ‎【答案】（1） （2），‎ ‎【解析】试题分析：（1）由向量数量积运算的几何意义知，向量在方向上的投影为，利用平面向量数量积公式求出,从而可结果；〔2〕先求得，再利用两个向量垂直的数量积为零列出关于的方程求解求得，从而解得.‎ 试题解析：因为，所以，向量在向量的方向上的投影为 ‎（2）因为，且， ‎ 因为，所以，，即，，‎ 解得，，此时，. ‎ ‎【方法点睛】本题主要考查向量的模及平面向量数量积公式、向量的投影，属于中档题. 平面向量数量积公式有两种形式，一是，二是，主要应用以下几个方面:(1)求向量的夹角， （此时往往用坐标形式求解）；（2）求投影， 在 上的投影是；（3）向量垂直则;(4)求向量 的模（平方后需求）.‎ ‎19. 过点作直线交轴正半轴于点、交轴正半轴于点 ‎（1）若时，求这条直线的方程；‎ ‎（2）求当三角形（其中为坐标原点）的面积为4时的直线的方程.‎ ‎【答案】（1）（2）‎ ‎【解析】试题分析：（1）设：，得，. 则，，利用， 列出关于的方程，求出，利用点斜式即可得结果；（2） ，由，解得，利用点斜式即可得结果.‎ 试题解析：（1）显然直线的斜率存在且，‎ 设：，得，. ‎ 则，，，由，‎ 得，，即 所以，所求直线的方程为或写成.‎ ‎（2）由题意知， ‎ ‎ ，‎ 则，解得. ‎ 此时直线的方程为或写成.‎ ‎20. 设等差数列的前项和为，，，对每个正整数，在与之间插入个3，得到一个新的数列.‎ ‎（1）求数列的通项公式；‎ ‎（2）求数列的前项和为.‎ ‎【答案】（1）（2）‎ ‎【解析】试题分析：（1）根据等差数列的，，列出关于首项、公差的方程组，解方程组可得与的值，从而可得数列的通项公式；〔2）只要把在数列的第几项确定，而其余的项都是3，那么确定了, 在与之间插入个，在与之间插入个，在与之间插入个，，在与之间插入个.数列中的项排在第 项,故,利用分组求和法结合等比数列的求和公式可得结果.‎ 试题解析：（1）由，解得 ， ‎ 所以，. ‎ ‎（2）只要把ak=3k+2在数列的第几项确定，而其余的项都是3，那么确定了,‎ 由题意知，在与之间插入个，在与之间插入个，在与之间插入个，，在与之间插入个. ‎ 所以， 数列中的项3k+2排在第(k+30+31+32+…+3k-2)=项,‎ 故 所以，当 ‎ ‎ 注意到，Tn可改写成 当，且时，‎ ‎ ‎ 综合，‎ ‎【方法点睛】本题主要考查等差数列的通项公式、等比数列的前 项和公式及分组求和的应用，属于中档题. 等差数列基本量的运算是等差数列的一类基本题型，数列中的五个基本量，一般可以“知二求三”，通过列方程组所求问题可以迎刃而解，另外，解等差数列问题要注意应用等差数列的性质（）与前 项和的关系.‎ ‎21. 已知圆的面积为，且与轴、轴分别交于两点.‎ ‎（1）求圆的方程；‎ ‎（2）若直线与线段相交，求实数的取值范围；‎ ‎（3）试讨论直线与（1）小题所求圆的交点个数.‎ ‎【答案】（1） （2）（3）见解析 ‎【解析】试题分析：（1）由，可得，从而可得圆的方程；（2）由（1）可得圆的方程），可求得两点的坐标，根据直线与线段相交，可得到两点在直线的异侧，列不等式求解即可；（3）先求出圆心坐标及圆的半径，根据圆心到直线的距离等于、大于、小于半径可确定直线与圆的交点个数.‎ 试题解析：（1）因为圆： ，则圆的半径，‎ 所以，，即 ‎ 所以，圆的方程为.‎ ‎（2）因为圆的方程为，所以，点、.‎ 由题意，直线：与线段相交，‎ 所以 ‎ ‎，解得；，‎ 所以实数的取值范围为. ‎ ‎（3）因为圆心到直线：的距离，‎ 当，即或时，直线与圆没有交点； ‎ 当，即或，直线与圆有一个交点;‎ 当，即时，直线与圆有两个交点 ‎ ‎ ‎ ‎