- 2021-04-15 发布 |
- 37.5 KB |
- 41页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届二轮复习9-7抛物线课件(全国通用)
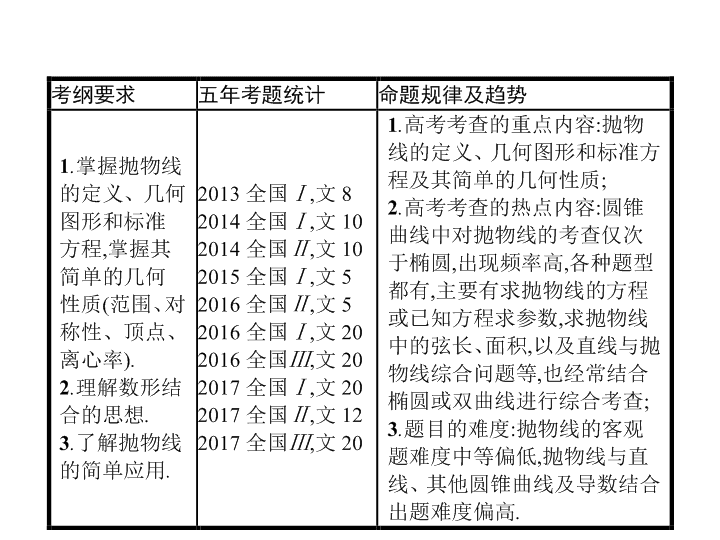
9 . 7 抛物线 - 2 - - 3 - 知识梳理 考点自测 1 . 抛物线的定义 平面内与一个定点 F 和一条定直线 l ( l 不经过点 F ) 的 的点的轨迹叫做抛物线 . 点 F 叫做抛物线的 , 直线 l 叫做抛物线的 . 2 . 抛物线的标准方程 (1) 顶点在坐标原点 , 焦点在 x 轴正半轴上的抛物线的标准方程为 ; (2) 顶点在坐标原点 , 焦点在 x 轴负半轴上的抛物线的标准方程为 ; (3) 顶点在坐标原点 , 焦点在 y 轴正半轴上的抛物线的标准方程为 ; (4) 顶点在坐标原点 , 焦点在 y 轴负半轴上的抛物线的标准方程为 . 距离相等 焦点 准线 y 2 = 2 px ( p> 0) y 2 =- 2 px ( p> 0) x 2 = 2 py ( p> 0) x 2 =- 2 py ( p> 0) - 4 - 知识梳理 考点自测 3 . 抛物线的几何性质 (0,0) y= 0 x= 0 1 - 5 - 知识梳理 考点自测 - 6 - 知识梳理 考点自测 1 . 设 AB 是过抛物线 y 2 = 2 px ( p> 0) 焦点 F 的弦 , 若 A ( x 1 , y 1 ), B ( x 2 , y 2 ), 如图所示 , 则 - 7 - 知识梳理 考点自测 1 . 判断下列结论是否正确 , 正确的画 “ √ ”, 错误的画 “ × ” . (1) 平面内与一个定点 F 和一条定直线 l 的距离相等的点的轨迹一定是抛物线 . ( ) (2) 若直线与抛物线只有一个交点 , 则直线与抛物线一定相切 . ( ) (3) 若一抛物线过点 P ( - 2,3), 则其标准方程可写为 y 2 = 2 px ( p> 0) . ( ) (4) 抛物线既是中心对称图形 , 又是轴对称图形 . ( ) (5) 方程 y=ax 2 ( a ≠0) 表示的曲线是焦点在 x 轴上的抛物线 , 且其焦点坐标是 . ( ) × × × × × - 8 - 知识梳理 考点自测 C 3 . (2017 安徽蚌埠一模 , 文 7) M 是抛物线 C : y 2 = 2 px ( p> 0) 上一点 , F 是抛物线 C 的焦点 , O 为坐标原点 , 若 |MF|=p , K 是抛物线 C 的准线与 x 轴的交点 , 则 ∠ MKO= ( ) A.15 ° B.30 ° C.45 ° D.60 ° C - 9 - 知识梳理 考点自测 4 . (2017 福建龙岩一模 , 文 14) 过抛物线 C : x 2 = 4 y 的焦点 F 作直线 l 交抛物线 C 于 A , B 两点 , 若 |AB|= 5, 则线段 AB 中点的纵坐标为 . 5 . 设 F 为抛物线 C : y 2 = 3 x 的焦点 , 过 F 且倾斜角为 30 ° 的直线交抛物线 C 于 A , B 两点 , 则 |AB|= . 12 - 10 - 考点一 考点二 考点三 考点四 考点五 抛物线的定义及其应用 C B - 11 - 考点一 考点二 考点三 考点四 考点五 - 12 - 考点一 考点二 考点三 考点四 考点五 思考 如何灵活应用抛物线的定义解决距离问题 ? 解题心得 1 . 由抛物线定义 , 把抛物线上点到焦点距离与到准线距离相互转化 . 2 . 注意灵活运用抛物线上一点 P ( x , y ) 到焦点 F 的距离 - 13 - 考点一 考点二 考点三 考点四 考点五 对点训练 1 (1)(2017 河南濮阳一模 , 文 9) 抛物线 y 2 = 2 px ( p> 0) 的焦点为圆 x 2 +y 2 - 6 x= 0 的圆心 , 过圆心且斜率为 2 的直线 l 与抛物线相交于 M , N 两点 , 则 |MN|= ( ) A.30 B.25 C.20 D.15 D C - 14 - 考点一 考点二 考点三 考点四 考点五 - 15 - 考点一 考点二 考点三 考点四 考点五 抛物线的方程及几何性质 B D - 16 - 考点一 考点二 考点三 考点四 考点五 - 17 - 考点一 考点二 考点三 考点四 考点五 - 18 - 考点一 考点二 考点三 考点四 考点五 思考 求抛物线标准方程的常用方法和关键是什么 ? 解题心得 1 . 求抛物线的标准方程主要利用待定系数法 , 因为抛物线方程有四种形式 , 所以在求抛物线方程时 , 需先定位 , 再定量 , 必要时要进行分类讨论 . 标准方程有时可设为 y 2 =mx 或 x 2 =my ( m ≠0) . 2 . 抛物线几何性质的确定 , 由抛物线的方程可以确定抛物线的开口方向、焦点位置、焦点到准线的距离 , 从而进一步确定抛物线的焦点坐标及准线方程 . - 19 - 考点一 考点二 考点三 考点四 考点五 对点训练 2 (1)(2017 宁夏银川模拟 ) 直线 l 过抛物线 x 2 = 2 py ( p> 0) 的焦点 , 且与抛物线交于 A , B 两点 , 若线段 AB 的长是 6, AB 的中点到 x 轴的距离是 1, 则此抛物线方程是 ( ) A. x 2 = 12 y B. x 2 = 8 y C. x 2 = 6 y D. x 2 = 4 y (2)(2017 广西玉林、贵港一模 , 文 15) 已知椭圆 与抛物线 y 2 = 2 px ( p> 0) 交于 A , B 两点 , |AB|= 2, 则 p= . B - 20 - 考点一 考点二 考点三 考点四 考点五 与抛物线相关的最值问题 (2) 已知 F 为抛物线 C : y 2 = 4 x 的焦点 , 过 F 作两条互相垂直的直线 l 1 , l 2 , 直线 l 1 与 C 交于 A , B 两点 , 直线 l 2 与 C 交于 D , E 两点 , 则 |AB|+|DE| 的最小值为 ( ) A.16 B.14 C.12 D.10 C A - 21 - 考点一 考点二 考点三 考点四 考点五 - 22 - 考点一 考点二 考点三 考点四 考点五 - 23 - 考点一 考点二 考点三 考点四 考点五 - 24 - 考点一 考点二 考点三 考点四 考点五 思考 求与抛物线有关的最值问题的一般思路是怎样的 ? 解题心得 与抛物线有关的最值问题的两个转化策略 转化策略一 : 将抛物线上的点到准线的距离转化为该点到焦点的距离 , 构造出 “ 两点之间线段最短 ”, 使问题得以解决 . 转化策略二 : 将抛物线上的点到焦点的距离转化为到准线的距离 , 利用 “ 与直线上所有点的连线中垂线段最短 ” 原理解决 . - 25 - 考点一 考点二 考点三 考点四 考点五 D 5 - 26 - 考点一 考点二 考点三 考点四 考点五 解析 : (1) 过点 M 作抛物线 y 2 = 2 x 左准线的垂线 , 垂足是 N ( 图略 ), 则 |MF|+|MA|=|MN|+|MA| , 当 A , M , N 三点共线时 , |MF|+|MA| 取得最小值 , 此时点 M 的坐标为 (2,2) . (2) 依题意 , 由点 M 向抛物线 x 2 = 4 y 的准线 l : y=- 1 作垂线 , 垂足为 M 1 ( 图略 ), 则有 |MA|+|MF|=|MA|+|MM 1 | , 则 |MA|+|MM 1 | 的最小值等于圆心 C ( - 1,5) 到 y=- 1 的距离再减去圆 C 的半径 , 即等于 6 - 1 = 5, 因此 |MA|+|MF| 的最小值是 5 . - 27 - 考点一 考点二 考点三 考点四 考点五 例 4 (1)(2017 天津 , 文 12) 设抛物线 y 2 = 4 x 的焦点为 F , 准线为 l , 已知点 C 在 l 上 , 以 C 为圆心的圆与 y 轴的正半轴相切于点 A , 若 ∠ FAC= 120 ° , 则圆的方程为 . 抛物线与其他圆锥曲线的综合 - 28 - 考点一 考点二 考点三 考点四 考点五 - 29 - 考点一 考点二 考点三 考点四 考点五 - 30 - 考点一 考点二 考点三 考点四 考点五 思考 求解抛物线与其他圆锥曲线的小综合问题要注意什么 ? 解题心得 求解抛物线与其他圆锥曲线的小综合问题 , 要注意距离的转换 , 将抛物线上的点到焦点的距离转换成抛物线上的点到准线的距离 , 这样可以简化运算过程 . - 31 - 考点一 考点二 考点三 考点四 考点五 对点训练 4 (1) 设抛物线 C : y 2 = 2 px ( p> 0) 的焦点为 F , 点 M 在 C 上 , |MF|= 5, 若以 MF 为直径的圆过点 (0,2), 则抛物线 C 的方程为 ( ) A. y 2 = 4 x 或 y 2 = 8 x B. y 2 = 2 x 或 y 2 = 8 x C. y 2 = 4 x 或 y 2 = 16 x D. y 2 = 2 x 或 y 2 = 16 x C D - 32 - 考点一 考点二 考点三 考点四 考点五 - 33 - 考点一 考点二 考点三 考点四 考点五 - 34 - 考点一 考点二 考点三 考点四 考点五 直线与抛物线的关系 例 5 (2017 河南南阳一模 , 文 20) 如图 , 抛物线 C : y 2 = 2 px 的焦点为 F , 抛物线上一定点 Q (1,2) . (1) 求抛物线 C 的方程及准线 l 的方程 ; (2) 过焦点 F 的直线 ( 不经过点 Q ) 与抛物线交于 A , B 两点 , 与准线 l 交于点 M , 记 QA , QB , QM 的斜率分别为 k 1 , k 2 , k 3 , 问是否存在常数 λ , 使得 k 1 +k 2 = λ k 3 成立 ? 若存在 λ , 求出 λ 的值 ; 若不存在 , 说明理由 . - 35 - 考点一 考点二 考点三 考点四 考点五 - 36 - 考点一 考点二 考点三 考点四 考点五 - 37 - 考点一 考点二 考点三 考点四 考点五 思考 求解抛物线综合问题的一般方法是怎样的 ? 解题心得 求解抛物线综合问题的方法 (1) 研究直线与抛物线的位置关系与研究直线与椭圆、双曲线的位置关系的方法类似 , 一般是用方程法 , 但涉及抛物线的弦长、中点、距离等问题时 , 要注意 “ 设而不求 ”“ 整体代入 ”“ 点差法 ” 以及定义的灵活应用 . (2) 有关直线与抛物线的弦长问题 , 要注意直线是否过抛物线的焦点 , 若过抛物线的焦点 , 可直接使用公式 |AB|=x 1 +x 2 +p ( 焦点在 x 轴正半轴 ), 若不过焦点 , 则必须用弦长公式 . - 38 - 考点一 考点二 考点三 考点四 考点五 对点训练 5 (2017 福建泉州一模 , 文 20) 在平面直角坐标系 xOy 中 , 抛物线 C : x 2 = 2 py ( p> 0) 的焦点为 F , 点 A 在抛物线 C 上 , 若 |AO|=|AF|= . (1) 求抛物线 C 的方程 ; (2) 设直线 l 与抛物线 C 交于点 P , Q , 若线段 PQ 的中点的纵坐标为 1, 求 △ OPQ 的面积的最大值 . - 39 - 考点一 考点二 考点三 考点四 考点五 - 40 - 考点一 考点二 考点三 考点四 考点五 1 . 认真区分四种形式的标准方程 : (1) 区分 y=ax 2 与 y 2 = 2 px ( p> 0), 前者不是抛物线的标准方程 . (2) 求抛物线标准方程要先确定形式 , 必要时要进行分类讨论 , 标准方程有时可设为 y 2 =mx 或 x 2 =my ( m ≠0) . 2 . 解决有关抛物线的焦点弦问题 , 熟记有关的常用结论是突破解题思路、提高解题速度的有效途径 . - 41 - 考点一 考点二 考点三 考点四 考点五 1 . 求抛物线的标准方程时一般要用待定系数法求 p 值 , 但首先要判断抛物线是不是标准方程 , 以及是哪一种标准方程 . 2 . 求过焦点的弦或与焦点有关的距离问题 , 要多从抛物线的定义入手 , 这样可以简化问题 .查看更多