- 2021-04-15 发布 |
- 37.5 KB |
- 5页

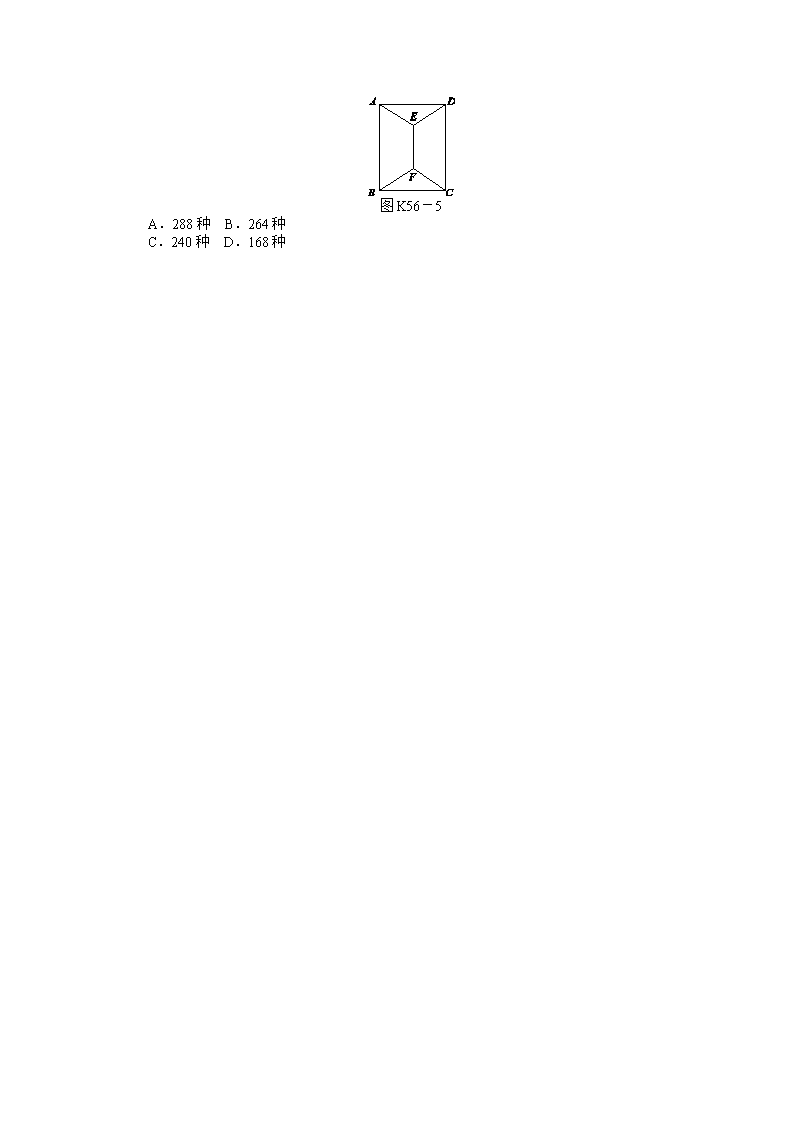
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教A版理科数学课时试题及解析(56)分类加法计数原理与分步乘法计数原理
课时作业(五十六) [第56讲 分类加法计数原理与分步乘法计数原理] [时间:45分钟 分值:100分] 1.从集合{0,1,2,3,4,5,6}中任取两个互不相等的数a,b组成复数a+bi,其中虚数有( ) A.30个 B.42个 C.36个 D.35个 2.教学大楼共有五层,每层均有两个楼梯,由一层到五层的走法有( ) A.10种 B.32种 C.25种 D.16种 3.记4名同学报名参加学校三个不同体育队,每人限报一队的不同报法种数为A;记3个班分别从5个风景点中选择一处游览的不同选法种数为B,则A,B分别是( ) A.43,53 B.34,35 C.34,53 D.43,35 4.设A,B是两个非空集合,定义A*B={(a,b)|a∈A,b∈B},若P={0,1,2},Q={1,2,3,4},则P*Q中元素的个数是( ) A.4 B.7 C.12 D.16 5.如图K56-1,用4种不同的颜色涂入图中的矩形A,B,C,D中,要求相邻的矩形涂色不同,则不同的涂法有( ) A B C D K56-1 A.72种 B.48种 C.24种 D.12种 6.甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中恰有1门相同的选法有( ) A.6种 B.12种 C.24种 D.30种 7.从0,2,4中取一个数字,从1,3,5中取两个数字,组成无重复数字的三位数,则所有不同的三位数的个数是( ) A.36 B.48 C.52 D.54 8. 将5名同学分到甲、乙、丙3个小组,若甲组至少两人,乙、丙组至少各一人,则不同的分配方案的种数为( ) A.80 B.120 C.140 D.50 9. 若自然数n使得作竖式加法n+(n+1)+(n+2)均不产生进位现象,则称n为“良数”.例如:32是“良数”,因为32+33+34不产生进位现象;23不是“良数”,因为23+24+25产生进位现象.那么小于1 000的“良数”的个数为( ) A.27 B.36 C.39 D.48 10.十字路口来往的车辆,如果不允许回头,共有________种行车路线. 11. 将1,2,3,…,9这9个数字填在如图K56-2所示的9个空格中,要求每一行从左到右,每一列从上到下分别依次增大,当3,4固定在图中的位置时,填写空格的方法数有________种. 3 4 图K56-2 12.学校安排4名教师在六天里值班,每天只安排一名教师,每人至少安排一天,至多安排两天,且这两天要相连,那么不同的安排方法有________种(用数字作答). 13. 用红、黄、蓝三种颜色之一去涂图K56-3中标号为1,2,…,9的9个小正方形,使得任意相邻(有公共边的)小正方形所涂颜色都不相同,且标号为1、5、9的小正方形涂相同的颜色,则符合条件的所有涂法共有________种. 1 2 3 4 5 6 7 8 9 图K56-3 14.(10分)有六名同学报名参加三个智力竞赛项目,在下列情况下各有多少种不同的报名方法? (1)每人恰好参加一项,每项人数不限; (2)每项限报一人,且每人至多参加一项; (3)每项限报一人,但每人参加的项目不限. 15.(13分)如图K56-4所示,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种颜色可供使用,求不同的染色方法总数. 图K56-4 16.(1)(6分) 现有6名同学去听同时进行的5个课外知识讲座,每名同学可自由选择其中的一个讲座,不同选法的种数是( ) A.56 B.65 C. D.6×5×4×3×2 (2)(6分) 如图K56-5所示,用四种不同颜色给图中的A、B、C、D、E、F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法共有( ) 图K56-5 A.288种 B.264种 C.240种 D.168种 课时作业(五十六) 【基础热身】 1.C [解析] b有6种取法,a也有6种取法,由分步乘法计数原理共可以组成6×6=36个虚数. 2.D [解析] 由分步乘法计数原理知有2×2×2×2=16(种)不同走法. 3.C [解析] 4名学生参加3个运动队,每人限报一个,可以报同一运动队,应该是人选运动队,所以不同的报法种数是34,故A=34;3个班分别从5个风景点中选择一处游览,应该是班选风景点,故不同的选法种数是53,故B=53. 4.C [解析] 由分步乘法计数原理知有3×4=12个. 【能力提升】 5.A [解析] 先分两类:一是四种颜色都用,这时A有4种涂法,B有3种涂法,C有2种涂法,D有1种涂法,共有4×3×2×1=24种涂法;二是用三种颜色,这时A,B,C的涂法有4×3×2=24种,D只要不与C同色即可,故D有2种涂法.故不同的涂法共有24+24×2=72种. 6.C [解析] 方法1:两人各选修2门的种数为CC=36,再求出两人所选两门都相同和都不同的种数均为C=6,故恰好有1门相同的选法有24种. 方法2:恰有1门相同,先从4门选1门,选法C,然后甲从剩下的3门选1门,乙再从甲选后剩下的2门中选1门,根据乘法原理共有选法4×3×2=24种. 7.B [解析] 若取出的数字含有0,则是2×A=12个,若取出的数字不含0,则是CCA=36个.根据加法原理得总数为48个. 8.A [解析] 分两类:若甲组2人,则乙、丙两组的方法数是CA,此时的方法数是CCA=60;若甲组3人,则方法数是CA=20.根据分类加法计数原理得总的方法数是60+20=80. 9.D [解析] 一位良数有0,1,2,共3个; 两位数的良数十位数可以是1,2,3,两位数的良数有10,11,12,20,21,22,30,31,32,共9个; 三位数的良数有百位为1,2,3,十位数为0的,个位可以是0,1,2,共3×3=9个,百位为1,2,3,十位不是零时,十位个位可以是两位良数,共有3×9=27个. 根据分类加法计数原理,共有48个小于1 000的良数. 10.12 [解析] 由分步乘法计数原理有4×3=12. 11.6 [解析] 左上方只能填1,右下方只能填9,此时4的上方只能填2.右上方填5时,其下方填6,7,8;右上方填6时,其下方填7,8;右上方填7时,其下方只能填8,此时左下方的两个格填法随之确定.故只能有3+2+1=6种填法. 12.144 [解析] 有两名教师要值班两天,把六天分为四份,两个两天连排的是(1,2),(3,4);(1,2),(4,5);(1,2),(5,6);(2,3),(4,5);(2,3),(5,6);(3,4),(5,6),共六种情况,把四名教师进行全排列,有A=24种情况,根据分步乘法计数原理,共有不同的排法6×24=144种. 13.108 [解析] 分步求解.只要在涂好1,5,9后,涂2,3,6即可,若3与1,5,9同色,则2,6的涂法为2×2,若3与1,5,9不同色,则3有两种涂法,2,6只有一种涂法,同理涂4,7,8,即涂法总数是C(2×2+C×1)×(2×2+C×1)=3×6×6=108. 14.[解答] (1)每人都可以从这三个比赛项目中选报一项,各有3种不同选法,由分步计数原理知共有方法36=729种. (2)每项限报一人,且每人至多限报一项,因此可由项目选人,第一个项目有6种选法,第二个项目有5种选法,第三个项目只有4种选法,由分步计数原理得共有报名方法6×5×4=120种. (3)由于每人参加的项目不限,因此每一个项目都可以从这六人中选出一人参赛,由分步乘法计数原理得共有不同的报名方法63=216种. 15.[解答] 方法一:可分为两大步进行,先将四棱锥一侧面三顶点染色,然后再分类考虑另外两顶点的染色数,用分步乘法原理即可得出结论. 由题设,四棱锥S—ABCD的顶点S、A、B所染的颜色互不相同,它们共有5×4×3= 60种染色方法. 当S、A、B染好时,不妨设其颜色分别为1、2、3,若C染2,则D可染3或4或5,有3种染法;若C染4,则D可染3或5,有2种染法;若C染5,则D可染3或4,有2种染法.可见,当S、A、B已染好时,C、D还有7种染法,故不同的染色方法有60×7=420种. 方法二:以S、A、B、C、D顺序分步染色. 第一步,S点染色,有5种方法; 第二步,A点染色,与S在同一条棱上,有4种方法; 第三步,B点染色,与S、A分别在同一条棱上,有3种方法; 第四步,C点染色,也有3种方法,但考虑到D点与S、A、C相邻,需要针对A与C是否同色进行分类,当A与C同色时,D点有3种染色方法;当A与C不同色时,因为C与S、B也不同色,所以C点有2种染色方法,D点也有2种染色方法. 由分步乘法、分类加法计数原理得不同的染色方法共有5×4×3×(1×3+2×2)=420种. 方法三:按所用颜色种数分类. 第一类,5种颜色全用,共有A种不同的方法; 第二类,只用4种颜色,则必有某两个顶点同色(A与C,或B与D),共有2×A种不同的方法; 第三类,只用3种颜色,则A与C、B与D必定同色,共有A种不同的方法. 由分类加法计数原理,得不同的染色方法总数为A+2×A+A=420种. 【难点突破】 16.(1)A (2)B [解析] (1)本题考查计数原理等有关知识,在高考考纲中为B级要求.因为每位同学均有5种讲座可选择,所以6位同学共有5×5×5×5×5×5=56种选择,故本题选A. (2)分三类:①B、D、E、F用四种颜色,则有A×1×1=24种方法; ②B、D、E、F用三种颜色,则有A×2×2+A×2×1×2=192种方法; ③B、D、E、F用两种颜色,则有A×2×2=48, 所以共有不同的涂色方法24+192+48=264种.查看更多