- 2021-04-15 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年八年级数学下册22微专题新定义问题习题(新版)冀教版
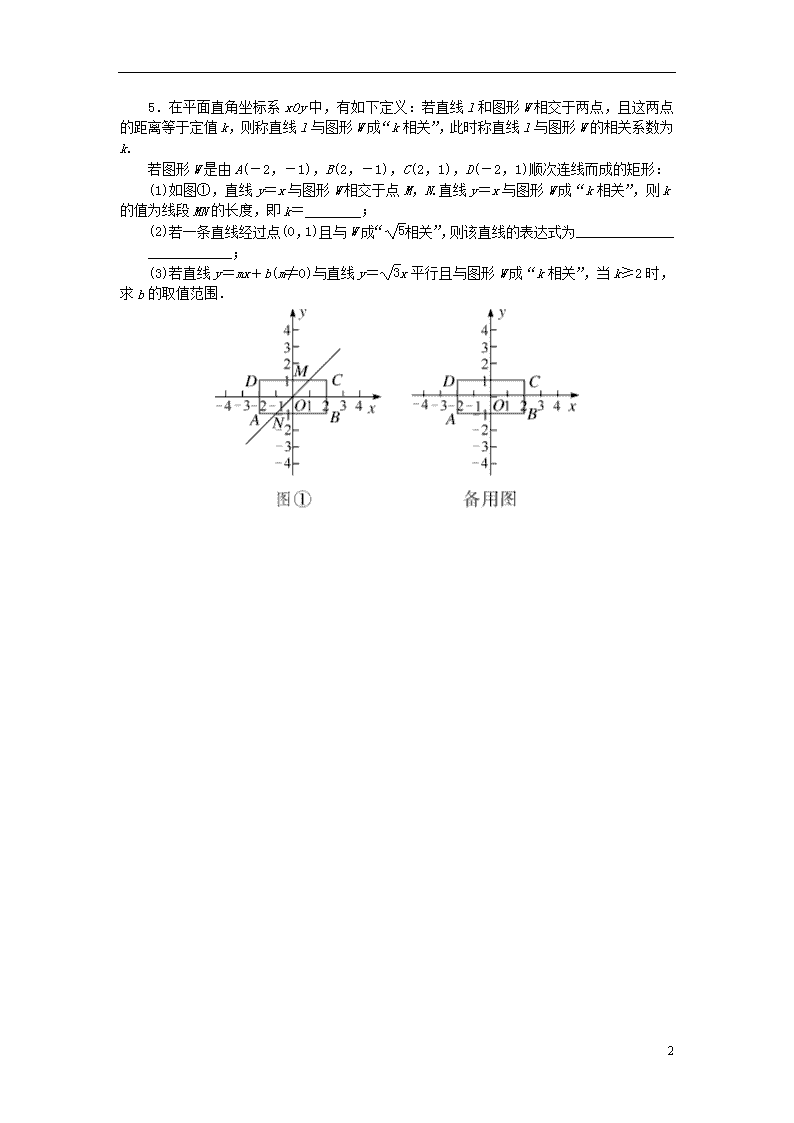
微专题:新定义问题【河北热点】 1.(2017·湘潭中考)阅读材料:设 =(x1,y1),=(x2,y2),如果 ∥,那么x1·y2=x2·y1.根据该材料填空:已知 =(2,3),=(4,m),若 ∥,则m=________. 2.(2017·吉林中考)我们规定:当k,b为常数,k≠0,b≠0,k≠b时,一次函数y=kx+b与y=bx+k互为交换函数.例如:y=4x+3的交换函数为y=3x+4.―次函数y=kx+2与它的交换函数图像的交点横坐标为________. 3.(2017·赤峰中考)在平面直角坐标系中,点P(x,y)经过某种变换后得到点P′(-y+1,x+2),我们把点P′(-y+1,x+2)叫作点P(x,y)的终结点.已知点P1的终结点为P2,点P2的终结点为P3,点P3的终结点为P4,这样依次得到P1、P2、P3、P4、…、Pn、…,若点P1的坐标为(2,0),则点P2017的坐标为________. 4.在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如:三点坐标分别为A(1,2),B(-3,1),C(2,-2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.根据所给定义解决下列问题: (1)若已知点D(1,2),E(-2,1),F(0,6),则这三点的“矩面积”为________. (2)若D(1,2),E(-2,1),F(0,t)三点的“矩面积”为18,求点F的坐标. 3 5.在平面直角坐标系xOy中,有如下定义:若直线l和图形W相交于两点,且这两点的距离等于定值k,则称直线l与图形W成“k相关”,此时称直线l与图形W的相关系数为k. 若图形W是由A(-2,-1),B(2,-1),C(2,1),D(-2,1)顺次连线而成的矩形: (1)如图①,直线y=x与图形W相交于点M,N.直线y=x与图形W成“k相关”,则k的值为线段MN的长度,即k=________; (2)若一条直线经过点(0,1)且与W成“相关”,则该直线的表达式为______________ ____________; (3)若直线y=mx+b(m≠0)与直线y=x平行且与图形W成“k相关”,当k≥2时,求b的取值范围. 3 参考答案与解析 1.6 2.1 3.(2,0) 解析:P1 坐标为(2,0),则P2坐标为(1,4),P3坐标为(-3,3),P4坐标为(-2,-1),P5坐标为(2,0),∴Pn的坐标为(2,0),(1,4),(-3,3),(-2,-1)循环.∵2017=2016+1=4×504+1,∴P2017 坐标与P1点相同,故答案为(2,0). 4.解:(1)15 (2)由题意可得a=1-(-2)=3,当t>2时,h=t-1,则3(t-1)=18,解得t=7,故点F的坐标为(0,7);当1≤t≤2时,h=2-1=1≠18÷3,故此种情况不符合题意;当t<1时,h=2-t,则3(2-t)=18,解得t=-4,故点F的坐标为(0,-4),所以,点F的坐标为(0,7)或(0,-4). 5.解:(1)2 (2)y=x+1或y=2x+1或y=-2x+1或y=-x+1 (3)∵直线y=mx+b(m≠0)与直线y=x平行,∴m=.∵k≥2,∴符合题意的临界直线分别经过点(-1,1),(1,-1),如图所示.当直线y=x+b过点(-1,1)时,有1=-+b,解得b=1+;当直线y=x+b过点(1,-1)时,有-1=+b,解得b=-1-.∴当k≥2时,b的取值范围为-1-≤b≤1+. 3查看更多