【物理】2020届一轮复习人教版圆周运动的案例分析课时作业
2020届一轮复习人教版 圆周运动的案例分析 课时作业
1.火车在某个弯道按规定运行速度40m/s转弯时,内、外轨对车轮皆无侧压力,若火车在该弯道实际运行速度为30m/s,则下列说法中正确的是( )
A.仅内轨对车轮有侧压力
B.仅外轨对车轮有侧压力
C.内、外轨对车轮都有侧压力
D.内、外轨对车轮均无侧压力
解析:火车在弯道按规定运行速度转弯时,重力和支持力的合力提供向心力,内、外轨对车轮皆无侧压力。若火车的运行速度小于规定运行速度时,重力和支持力的合力大于火车需要的向心力,内轨对车轮产生侧压力,重力、支持力和内轨的侧压力的合力提供火车做圆周运动的向心力,故A正确。
答案:A
2.
赛车在倾斜的轨道上转弯如图所示,弯道的倾角为θ,半径为R,则赛车完全不靠摩擦力转弯的速率是(设转弯半径水平)( )
A. B.
C. D.
解析:
赛车受力分析如图所示,可见:F合=Gtanθ=mgtanθ,而F合=m,故v=。
答案:C
3.
如图所示,质量为m的小球固定在长为L的细杆一端,绕细杆的另一端O在竖直平面内做圆周运动,球转到最高点A时,线速度的大小为,则( )
A.细杆受到的拉力 B.细杆受到的压力
C.细杆受到的拉力 D.细杆受到的压力
解析:小球在最高点线速度为,所需向心力为F=,向心力的方向向下,重力的方向也向下,重力的一半提供向心力,剩余的重力是杆对小球的支持力与其平衡,也就是杆对小球有的支持力,由牛顿第三定律得小球对杆有的压力。
答案:B
4.
一辆满载的卡车在起伏的公路上匀速行驶,如图所示,由于轮胎过热,容易爆胎。爆胎可能性最大的地段是( )
A.A处 B.B处
C.C处 D.D处
解析:在A、B、C、D各点均由重力与支持力的合力提供向心力,爆胎可能性最大的地段为轮胎与地面的挤压力最大处。在A、C两点有mg-F=m,则F=mg-m
mg,且R越小,F越大,故FD最大,即D处最容易爆胎。
答案:D
5.(多选)如图所示,汽车以速度v通过一弧形的拱桥顶端时,关于汽车受力的说法中正确的是( )
A.汽车的向心力就是它所受的重力
B.汽车的向心力是它所受的重力与支持力的合力,方向指向圆心
C.汽车受重力、支持力、牵引力、摩擦力和向心力的作用
D.汽车受到的支持力比重力小
解析:汽车以速度v通过一弧形的拱桥顶端时,受重力、支持力、牵引力和摩擦力,重力与支持力的合力提供向心力,方向指向圆心,A、C错误,B正确;汽车受到的支持力比重力小,D正确。
答案:BD
6.(多选)如图所示,小球m在竖直放置的光滑的圆形管道内做圆周运动,下列说法正确的是( )
A.小球通过最高点时的最小速度是
B.小球通过最高点时的最小速度为零
C.小球通过最低点时对管壁压力一定大于重力
D.小球在水平线ab以上的管道中运动时外侧管壁对小球一定有作用力
解析:小球在光滑的圆形管道内运动到最高点时的最小速度为零,A错误,B正确;小球通过最低点时N-mg=m得N=mg+m,故小球通过最低点时对管壁的压力一定大于重力,C正确;小球在水平线ab以上的管道中运动时外侧管壁对小球不一定有作用力,D错误。
答案:BC
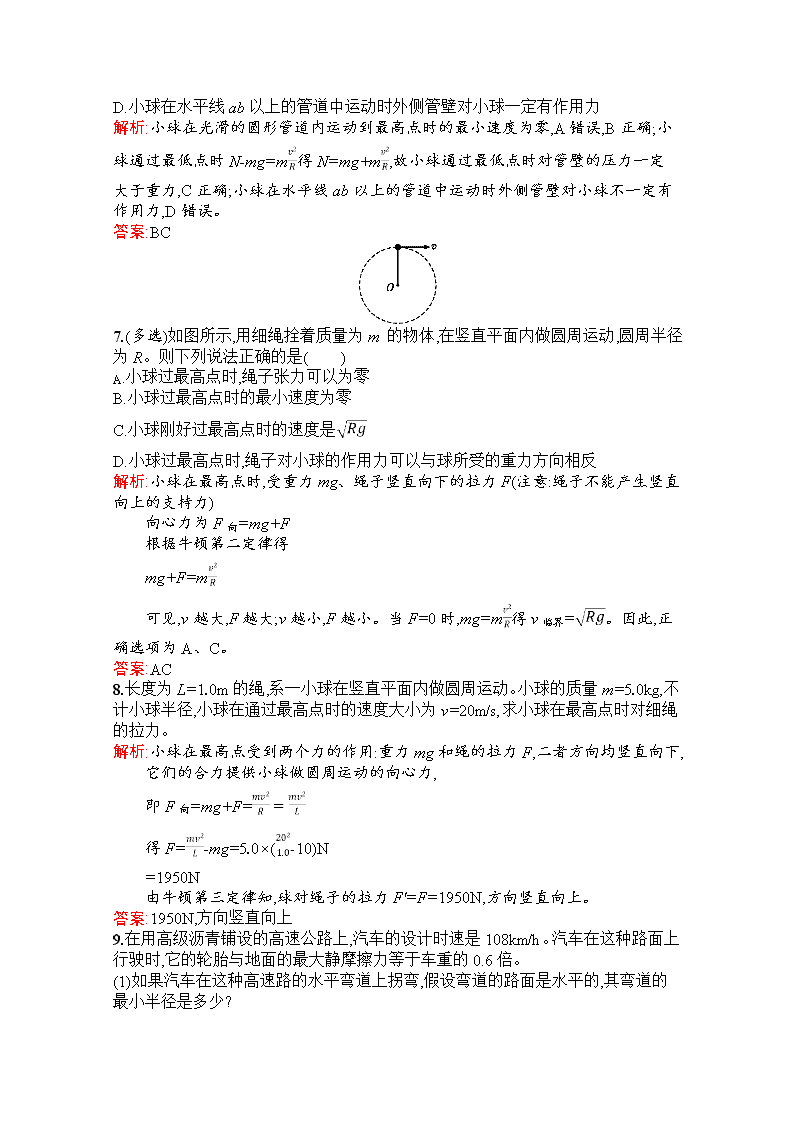
7.(多选)如图所示,用细绳拴着质量为m 的物体,在竖直平面内做圆周运动,圆周半径为R。则下列说法正确的是( )
A.小球过最高点时,绳子张力可以为零
B.小球过最高点时的最小速度为零
C.小球刚好过最高点时的速度是
D.小球过最高点时,绳子对小球的作用力可以与球所受的重力方向相反
解析:小球在最高点时,受重力mg、绳子竖直向下的拉力F(注意:绳子不能产生竖直向上的支持力)
向心力为F向=mg+F
根据牛顿第二定律得
mg+F=m
可见,v越大,F越大;v越小,F越小。当F=0时,mg=m得v临界=。因此,正确选项为A、C。
答案:AC
8.长度为L=1.0m的绳,系一小球在竖直平面内做圆周运动。小球的质量m=5.0kg,不计小球半径,小球在通过最高点时的速度大小为v=20m/s,求小球在最高点时对细绳的拉力。
解析:小球在最高点受到两个力的作用:重力mg和绳的拉力F,二者方向均竖直向下,
它们的合力提供小球做圆周运动的向心力,
即F向=mg+F=
得F=-mg=5.0×(-10)N
=1950N
由牛顿第三定律知,球对绳子的拉力F'=F=1950N,方向竖直向上。
答案:1950N,方向竖直向上
9.在用高级沥青铺设的高速公路上,汽车的设计时速是108km/h。汽车在这种路面上行驶时,它的轮胎与地面的最大静摩擦力等于车重的0.6倍。
(1)如果汽车在这种高速路的水平弯道上拐弯,假设弯道的路面是水平的,其弯道的最小半径是多少?
(2)如果高速路上设计了圆弧拱桥做立交桥,要使汽车能够以设计时速安全通过圆弧拱桥,这个圆弧拱桥的半径至少是多少?(g取10m/s2)
解析:(1)汽车在水平路面上拐弯,可视为汽车做匀速圆周运动,其向心力由车与路面间的静摩擦力提供,当静摩擦力达到最大值时,由向心力公式可知这时的半径最小,有
fmax=0.6mg≥m,由速度v=30 m/s,得弯道半径R≥150m。
(2)汽车过拱桥,看作在竖直平面内做匀速圆周运动,到达最高点时,根据向心力公式有
mg-N=m,为了保证安全,车对路面间的弹力必须大于等于零。有
mg≥m,则R≥90m。
答案:(1)150m (2)90 m