- 2021-04-15 发布 |
- 37.5 KB |
- 15页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
陕西省渭南市韩城市司马迁中学2020届高三全国统一招生考试数学(理)试卷 (1)
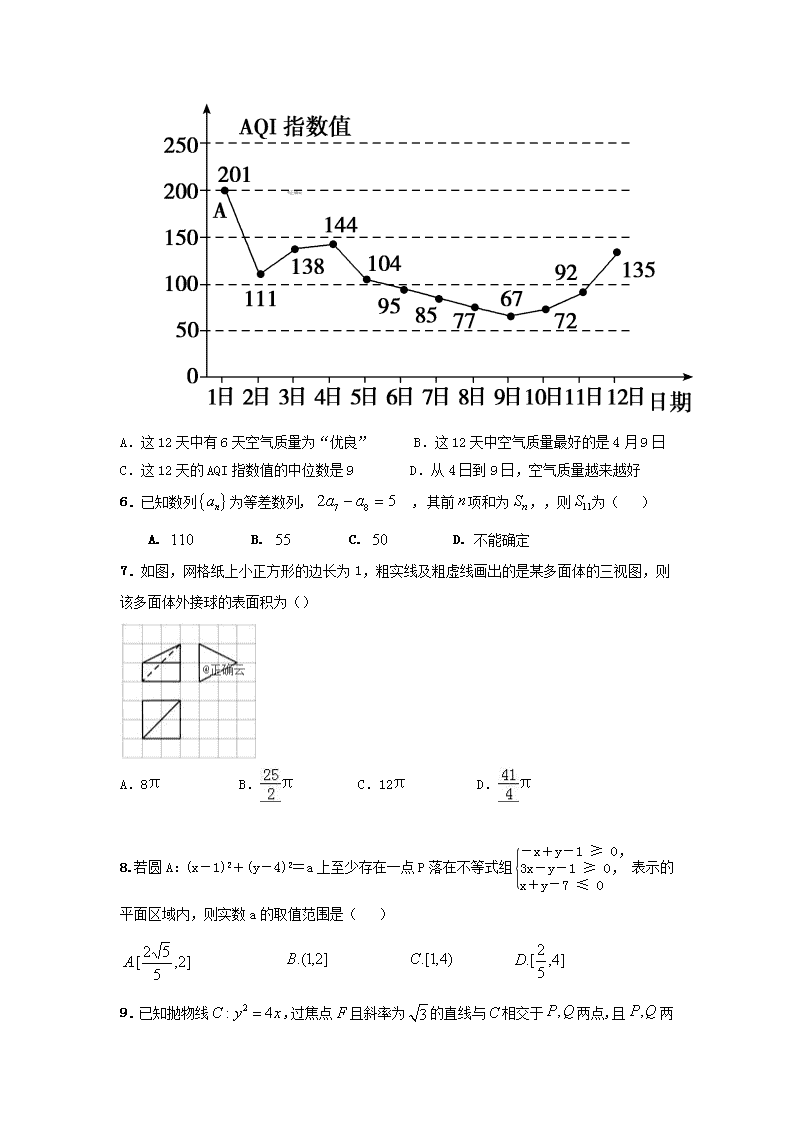
数学(理) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。考生作答时,将答案答在答题卡上,在本试卷上答题无效。考试结束后,将本试卷和答题卡一并交回。 注意事项: 1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并帖好条形码。请认真核准条形码的准考证号、姓名和科目。 2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。 第Ⅰ卷 一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合,, 则( ) A. B. C. D. 2.若(为虚数单位,),则等于( ) A. -2 B. -1 C. 1 D. 2 ( ) 4.某产品的广告费用x与销售额y的统计数据如下表 广告费用x(百元) 1 2 3 4 销售额y(万元) 0.1 1.8 m 4 根据上表可得回归方程, 则m= A.2.9 B.3.0 C.3.1 D.2.8 5.AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是() A.这12天中有6天空气质量为“优良” B.这12天中空气质量最好的是4月9日 C.这12天的AQI指数值的中位数是9 D.从4日到9日,空气质量越来越好 6.已知数列为等差数列, , 其前项和为,,则为( ) A. B. C. D. 不能确定 7.如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为() A.8π B.π C.12π D.π 8.若圆A:(x-1)2+(y-4)2=a上至少存在一点P落在不等式组表示的平面区域内,则实数a的取值范围是( ) 9.已知抛物线,过焦点且斜率为的直线与相交于两点,且 两点在准线上的投影分别为两点,则( ) A. B. C. D. 10.函数的图像大致是( ) A. B. C. D. 11.若对圆上任意一点,的取值与无关,则实数的取值范围是( ) A. B. C. 或 D. 12.已知关于x的不等式x(x-m)>m有且仅有三个正整数解(其中e=2.71828…为自然对数的底数),则实数m的取值范围是 A.(,] B.(,] C.[,) D.[,) 第Ⅱ卷(非选择题部分,共90分) 本卷包括必考题和选考题两个部分. 第13题~第21题为必考题,每个考生都必须作答. 第22题~第23题为选考题,考生根据要求作答. 二.填空题:本大题共4小题,每小题5分,共20分. 13.13、已知向量 =(3,﹣1), =(2,1),则 在 方向上的投影为________. 14.设,则含x的项为 . 15.《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体, 下底面宽丈,长丈;上棱长丈,无宽,高丈(如图). 问它的体积是多少? ”这个问题的答案是( ) 16.在锐角三角形ABC中,角A,B,C所对的边分别为a,b,c,a=1,且(bc﹣2)cosA+accosB=1﹣b2,则△ABC面积的最大值为 . 三.解答题:本大题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分已知数列{an}的前n项和为Sn,且, (1)求数列{an}的通项公式; (2)若数列的前n项和为Tn,证明:Tn<4. 18.(本小题满分12分)已知四棱锥中,底面是边长为的菱形,, ,点是棱的中点,点在棱上,且,//平面. (Ⅰ)求实数的值; (Ⅱ)求二面角的余弦值. 19.(本小题满分12分)近年来随着我国在教育科研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓,国内有实力企业纷纷进行海外布局,第二轮企业出海潮到来.如在智能手机行业,国产品牌已在赶超国外巨头,某品牌手机公司一直默默拓展海外市场,在海外共设多个分支机构,需要国内公司外派大量后、后中青年员工.该企业为了解这两个年龄层员工是否愿意被外派工作的态度,按分层抽样的方式从后和后的员工中随机调查了位,得到数据如下表: 愿意被外派 不愿意被外派 合计 后 后 合计 (Ⅰ)根据调查的数据,是否有以上的把握认为“是否愿意被外派与年龄有关”,并说明理由; (Ⅱ)该公司举行参观驻海外分支机构的交流体验活动,拟安排名参与调查的后、后员工参加.后员工中有愿意被外派的人和不愿意被外派的 人报名参加,从中随机选出人,记选到愿意被外派的人数为;后员工中有愿意被外派的人和不愿意被外派的人报名参加,从中随机选出人,记选到愿意被外派的人数为,求的概率. 参考数据: (参考公式:,其中) x y F 2 F 1 P N M B A O 20.(本小题满分12分)如图,椭圆的右顶点为,左、右焦点分别为、,过点且斜率为的直线与轴交于点, 与椭圆交于另一个点,且点在轴上的射影恰好为点. (Ⅰ)求椭圆的标准方程; (Ⅱ)过点且斜率大于的直线与椭圆交于两点 (),若,求实数的取值范围. 21.(本小题满分12分)已知函数f(x)=ln(x+1)+ax2 , a>0. (1)讨论函数f(x)的单调性; (2)若函数f(x)在区间(﹣1,0)有唯一零点x0 , 证明: 请考生在第(22)、(23)两题中任选一题作答,如果多做,则按所做的第一题记分,作答时用2B铅笔在答题卡上把所选题目的题号涂黑,把答案填在答题卡上. 22.(本小题满分10分)选修4-4:坐标系与参数方程 在平面直角坐标系xOy中,曲线C的参数方程为(r>0, φ为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为=1,若直线l与曲线C相切. (Ⅰ)求曲线C的极坐标方程; (Ⅱ)在曲线C上取两点M,N与原点O构成△MON,且满足∠MON=,求△MON面积的最大值. 23.(本小题满分10分)选修4-5:不等式选讲 已知. (Ⅰ)求不等式的解集; (Ⅱ)若存在,使得成立,求实数的取值范围. 理科数学参考答案及评分标准(二) 一、选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的. 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D B B C C B D D B A D C 1、D【解析】因为,. 所以,故答案选D. 2.B.【解析】因为,则.所以 3. B 4.C 5.解析:选C.这12天中,空气质量为“优良”的有95,85,77,67,72,92,故A正确;这12天中空气质量最好的是4月9日,AQI指数值为67,故B正确;这12天的AQI指数值的中位数是=99.5,故C不正确;从4日到9日,空气质量越来越好,故D正确,故选C. 6.B【解析】,.故答案选B. 7.【解答】解:根据三视图得出:该几何体是镶嵌在正方体中的四棱锥O﹣ABCD,正方体的棱长为2,A,D为棱的中点 根据几何体可以判断:球心应该在过A,D的平行于底面的中截面上, 设球心到截面BCO的距离为x,则到AD的距离为:2﹣x, ∴R2=x2+()2,R2=12+(2﹣x)2, 解得出:x=,R=, 该多面体外接球的表面积为:4πR2=π, 故选:D. 8.【解析】圆D与不等式组表示的平面区域有交点,作出图象后易求得a的取值范围是. 9.B【解析】由题意可得直线与抛物线联解得:, 所以点,,则.在中,边上的高,则,故答案选B. 方法二:不防设交点在轴上方,由抛物线焦点弦性质得, 且, ,故,, 所以,故答案选B. 10.A【解析】因为函数可化简为可知函数为奇函数关于原点对称,可排除答案C;同时有 ,则当 ,可知函数在处附近单调递增,排除答案B和D,故答案选A. 11.D【解析】要使符合题意,则圆上所有点在直线之间, 因为圆心到直线的距离且,则所有圆心到直线的距离,且,解得,故答案选D. 12.答案C 【解析】依题意,,故,即,令,故,故当时,,当时,,当时,,作出函数的图象如下所示,可知三个正整数解为1,2,3;令,则,,解得,故选C. 二.填空题:本大题共4小题,每小题5分,共20分. 13.【答案】 【解析】【解答】解: =6﹣1=5,| |= , ∴ 在 方向上的投影为| |cos<cos >=| | = = = . 故答案为: . 14.x【解析】,所以 =-240x,故答案为-240x. 15. 立方丈 将该几何体分成一个直三棱柱,两个四棱锥, 即, 16.【解答】解:∵a=1,且(bc﹣2)cosA+accosB=1﹣b2, ∴(bc﹣2)•+ac•=1﹣b2, 即﹣+=1﹣b2, 即﹣+c2=1﹣b2, 即﹣+c2+b2﹣1=0, ﹣+c2+b2﹣a2=0, 即(c2+b2﹣a2)(1﹣)=0, ∵△ABC是锐角三角形形, ∴cosA=>0,即c2+b2﹣a2>0, 则1﹣=0,即bc=1, 由余弦定理得a2=b2+c2﹣2bccosA≥2bc﹣2bccosA, 即1≥2﹣2cosA, 得2cosA≥1,得cosA≥,即0°<A≤60°, 则三角形的面积S=bcsinA≤×=, 即三角形面积的最大值为, 故答案为: 三.解答题:本大题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤. 17.【解答】解:(1)当n=1时,2S1=a1+2a1﹣1,即a1=1,……(1分) 当n≥2时,2Sn=nan+2an﹣1①,2Sn﹣1=(n﹣1)an﹣1+2an﹣1﹣1②……(2分) ①﹣②,得2an=nan﹣(n﹣1)an﹣1+2an﹣2an﹣1,即nan=(n+1)an﹣1,…(3分) 所以,且,……………………………………………………………………(4分) 所以数列为常数列,…………………………………………………………………(5分) ,即.………………………………………………………(6分) (2)由(1)得,所以,………………(8分) 所以,………………………………………………………(9分) ,…………(没写也不扣分)………………………(10分) =………………………………………(11分) =.………………………………………………………………………(12分) 18.【解析】(Ⅰ)连接,设, 则平面平面, 平面,, ,, ,; (Ⅱ), 又, ,,平面, 以所在直线分别为轴,轴,轴建立空间直角坐标系,则,平面的法向量, 设平面的法向量, 则, , 令,得,,即所求二面角的余弦值是. ………………(12分) 19.【解析】(Ⅰ) 所以有90% 以上的把握认为“是否愿意被外派与年龄有关”……………………………(5分) (Ⅱ)“”包含:“”、 “”、 “”、 “”、 “”、 “”六个互斥事件 且, , , 所以: .………………(12分) 20.【解析】(Ⅰ)因为轴,得到点, 所以 ,所以椭圆的方程是.………………(4分) (Ⅱ)因为, 所以.由(Ⅰ)可知,设方程,, 联立方程得:.即得(*) 又,有, 将代入(*)可得:. 因为,有, 则且. 综上所述,实数的取值范围为. ………………(12分) 21、【答案】(1)解: ,x>﹣1, 令g(x)=2ax2+2ax+1,△=4a2﹣8a=4a(a﹣2), 若△<0,即0<a<2,则g(x)>0, 当x∈(﹣1,+∞)时,f'(x)>0,f(x)单调递增, 若△=0,即a=2,则g(x)≥0,仅当 时,等号成立, 当x∈(﹣1,+∞)时,f'(x)≥0,f(x)单调递增. 若△>0,即a>2,则g(x)有两个零点 , , 由g(﹣1)=g(0)=1>0, 得 , 当x∈(﹣1,x1)时,g(x)>0,f'(x)>0,f(x)单调递增; 当x∈(x1 , x2)时,g(x)<0,f'(x)<0,f(x)单调递减; 当x∈(x2 , +∞)时,g(x)>0,f'(x)>0,f(x)单调递增. 综上所述, 当0<a≤2时,f(x)在(﹣1,+∞)上单调递增; 当a>2时,f(x)在 和 上单调递增, 在 上单调递减 (2)解:由(1)及f(0)=0可知:仅当极大值等于零,即f(x1)=0时,符合要求. 此时,x1就是函数f(x)在区间(﹣1,0)的唯一零点x0 . 所以 ,从而有 , 又因为 ,所以 , 令x0+1=t,则 , 设 ,则 , 再由(1)知: ,h'(t)<0,h(t)单调递减, 又因为 , , 所以e﹣2<t<e﹣1 , 即 22.【解析】(Ⅰ)由题意可知直线l的直角坐标方程为y=x+2, 曲线C是圆心为,半径为r的圆,直线l与曲线C相切,可得: r==2;可知曲线C的方程为+=4, 所以曲线C的极坐标方程为ρ2-2ρcos θ-2ρsin θ=0,即ρ=4sin.(5分) (Ⅱ)由(Ⅰ)不妨设M(ρ1,θ),N,(ρ1>0,ρ2>0), S△MON=sin, =ρ1·ρ2=4sin·sin=2sin θcos θ+2cos2 θ =sin 2θ+cos 2θ+=2sin+, 当θ=时, S△MON=2+,所以△MON面积的最大值为2+.(10分) 23.【解析】(Ⅰ)不等式等价于或 或 ,解得或, 所以不等式的解集是; (Ⅱ),, ,解得实数的取值范围是.查看更多