江苏省淮安市楚中新马清浦洪泽高中四校2020届高三上学期期中联考数学（文）试题

江苏省淮安市楚中新马清浦洪泽高中四校2020届高三上学期期中联考数学（文）试题

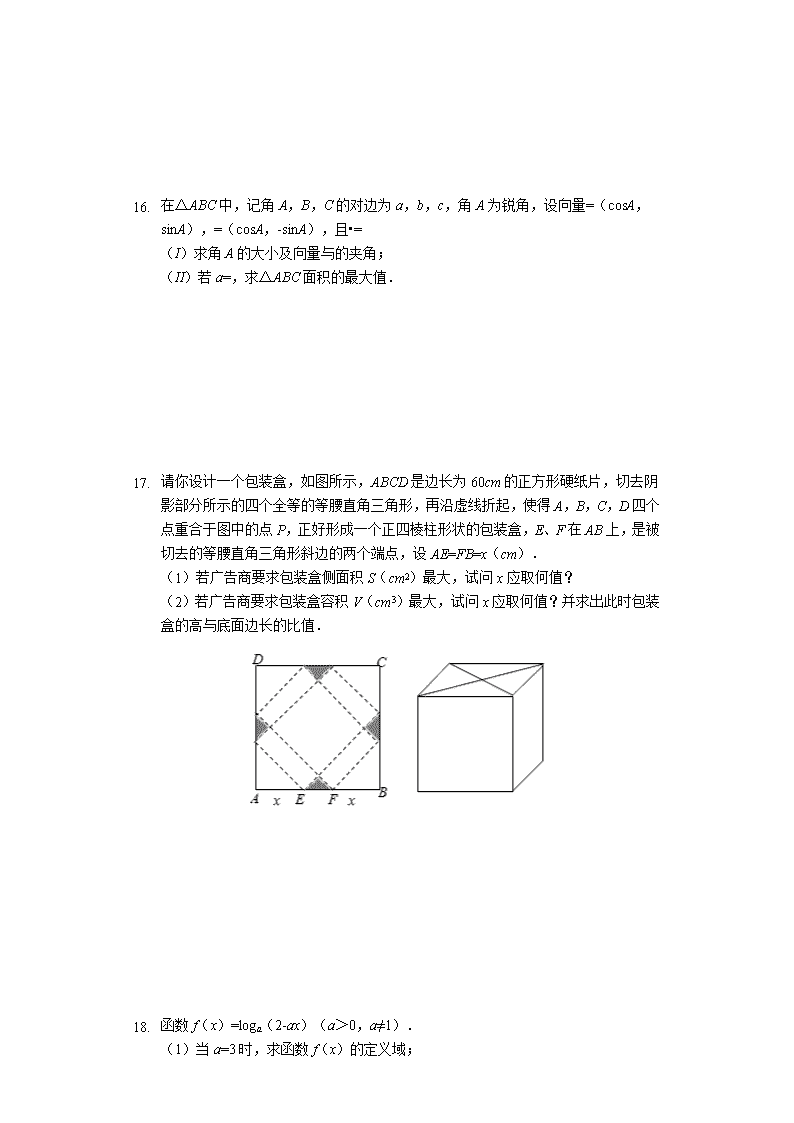
‎2019-2020学年度上学期期中考试高三数学试卷（文）‎ 一、填空题（本大题共14小题）‎ 1. 已知R为实数集，集合A={-1，0，1}，集合B={x|x≤0}，则A∩∁RB=______．‎ 2. ‎“∀x∈R，x2+2x+1＞‎0”‎的否定是______．‎ 3. 已知向量，若，则=______．‎ 4. 已知函数，则函数的最小正周期为______．‎ 5. 已知函数，则f（f（0）-3）=______．‎ 6. 设△ABC的内角A，B，C的对边分别为a，b，c，且a=2，cosC=-，3sinA=2sinB，则c=______．‎ 7. 已知，，则tanα=______．‎ 8. 将函数f（x）=cos（x+φ）（|φ|＜）的图象上各点的横坐标缩短到原来的倍（纵坐标不变），再把得到的图象向左平移个单位长度，所得函数图象关于原点对称，则φ=______．‎ 9. 若等比数列{an}的前n项和Sn=2n+1+c，则c=______．‎ 10. ‎《算法统宗》中有如下问题：“哑子来买肉，难言钱数目，一斤少三十，八两多十八，试问能算者，合与多少肉”，意思是一个哑子来买肉，说不出钱的数目，买一斤（两）还差文钱，买八两多十八文钱，求肉数和肉价，则该问题中，肉价是每两__________文．‎ 11. 在△ABC中，M是BC的中点，AM=3，BC=10，则•=______．‎ 12. 已知函数f（x）=xlnx-x2-x+a（a∈R）在其定义域内有两个不同的极值点，则实数a的取值范围是______．‎ 13. 已知a，b为正实数，直线y=x-a与曲线y=ln（x+b）相切，则+的最小值为______．‎ 14. 已知关于x的不等式（x-3）lnx≤2λ有解，则整数λ的最小值为______．‎ 二、解答题（本大题共6小题）‎ 15. 已知sin（α+）=，α∈（，π）． 求：（1）cosα的值； （2）sin（2α-）的值． ‎ 1. 在△ABC中，记角A，B，C的对边为a，b，c，角A为锐角，设向量=（cosA，sinA），=（cosA，-sinA），且•= （I）求角A的大小及向量与的夹角； （II）若a=，求△ABC面积的最大值． ‎ 2. 请你设计一个包装盒，如图所示，ABCD是边长为‎60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A，B，C，D四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E、F在AB上，是被切去的等腰直角三角形斜边的两个端点，设AE=FB=x（cm）． （1）若广告商要求包装盒侧面积S（cm2）最大，试问x应取何值？ （2）若广告商要求包装盒容积V（cm3）最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值．‎ ‎ ‎ 3. 函数f（x）=loga（2-ax）（a＞0，a≠1）． （1）当a=3时，求函数f（x）的定义域； （2）若 g（x）=f（x）-loga（2+ax），判断g（x）的奇偶性； （3）是否存在实数a，使函数f（x）在[2，3]递增，并且最大值为1，若存在，求出a的值；若不存在，说明理由． ‎ 1. 已知数列{an}和{bn}满足a‎1a2a3…an=（n∈N*）．若{an}为等比数列，且a1=2，b3=6+b2． （Ⅰ）求an和bn； （Ⅱ）设cn=（n∈N*）．记数列{cn}的前n项和为Sn．   （i）求Sn；  （ii）求正整数k，使得对任意n∈N*均有Sk≥Sn． ‎ 2. 已知函数f（x）=x2+ax+1，g（x）=ex（其中e为自然对数的底数）． （Ⅰ）若a=1，求函数y=f（x）•g（x）在区间[-2，0]上的最大值； （Ⅱ）若a=-1，关于x的方程f（x）=k•g（x）有且仅有一个根，求实数k的取值范围； （Ⅲ）若对任意的x1，x2∈[0，2]，x1≠x2，不等式|f（x1）-f（x2）|＜|g（x1）-g（x2）|均成立，求实数a的取值范围． ‎ 答案和解析 ‎1.【答案】{1} ‎ ‎【解析】解：∵A={-1，0，1}，B={x|x≤0}， ∴∁RB={x|x＞0}，A∩∁RB={1}． 故答案为：{1}． 进行补集、交集的运算即可． 考查列举法、描述法的定义，以及交集、补集的运算． 2.【答案】∃x0∈R，x02+2x0+1≤0 ‎ ‎【解析】解：命题为全称命题，则“∀x∈R，x2+2x+1＞‎0”‎的否定是：∃x0∈R，x02+2x0+1≤0， 故答案为：∃x0∈R，x02+2x0+1≤0． 根据含有量词的命题的否定即可得到结论． 本题主要考查含有量词的命题的否定，比较基础． 3.【答案】 ‎ ‎【解析】解：向量，若， ∴， ∴x=4， ==． 故答案为：． 利用斜率的垂直求出x，得到向量，然后求模即可． 本题考查斜率的数量积的应用，向量的模的求法，考查计算能力． 4.【答案】π ‎ ‎【解析】解：函数的最小正周期为：=π． 故答案为：π． 直接利用三角函数的周期公式求解即可． 本题考查三角函数的周期公式的应用，是基础题． 5.【答案】-1 ‎ ‎【解析】解：∵函数， ∴f（0）=e0=1， f（0）-3=1-3=-2＜0， ∴f（-2）=-2+1=-1‎ ‎， 所以f（f（0）-3）=f（-2）=-1， 故答案为-1； 已知f（x）是分段函数，代入分段函数求出f（0），再把f（0）-3看为一个整体，再进行代入进行求解； 此题主要考查分段函数的性质，注意分段函数的定义域，此题是一道基础题； 6.【答案】4 ‎ ‎【解析】解：∵3sinA=2sinB， ∴由正弦定理可得：‎3a=2b， ∵a=2， ∴可解得b=3， 又∵cosC=-， ∴由余弦定理可得：c2=a2+b2-2abcosC=4+9-2×=16， ∴解得：c=4． 故答案为：4． 由3sinA=2sinB即正弦定理可得‎3a=2b，由a=2，即可求得b，利用余弦定理结合已知即可得解． 本题主要考查了正弦定理，余弦定理在解三角形中的应用，属于基础题． 7.【答案】 ‎ ‎【解析】解：∵，∴∈（，）， 又，∴sin（）==． ∴sinα=sin[（）-]=sin（）cos-cos（）sin ==，则cosα=， ∴tan． 故答案为：． 由已知求得sin（），再由sinα=sin[（）-]，运用两角差的正弦展开求得sinα，然后利用同角三角函数基本关系式求解． 本题考查三角函数的化简求值，考查同角三角函数基本关系式与两角差的三角函数，是基础题． 8.【答案】 ‎ ‎【解析】解：将函数f（x）=cos（x+φ）（|φ|＜）的图象上各点的横坐标缩短到原来的倍（纵坐标不变）， 得到y=cos（2x+φ）， 再把得到的图象向左平移个单位长度，得到y=cos[2（x+）+φ]=cos（2x++φ）， ∵所得函数图象关于原点对称， ∴+φ=+kπ，k∈Z， 即φ=+kπ，k∈Z， ∵|φ|＜， ‎ ‎∴当k=0时，φ=， 故答案为：． 根据函数平移变换关系求出函数解析式，结合函数奇偶性的性质进行求解即可． 本题主要考查三角函数的图象和性质，结合三角函数的图象变换求出函数的解析式，以及利用函数对称性的性质是解决本题的关键． 9.【答案】-2 ‎ ‎【解析】【解答】 解：依题意，该等比数列的公比不为1， 所以Sn==-·qn=c+2×2n， 所以q=2，=-2， ∴c==-2， 故填：-2． 【分析】 显然该等比数列的公比不为1，所以Sn==-·qn=c+2×2n，所以q=2，=-2，c=-2， 本题考查了等比数列的前n项和，主要考查公式的运用和处理能力，属于基础题． 10.【答案】6 ‎ ‎【解析】【分析】 本题考查中国古代著作中的数学问题，属数学文化，正确地理解题意是解题关键． 设肉价是每两x文，根据题意列出方程可解得答案 【解答】 解：设肉价是每两x文，由题意得16x-30=8x+18，解得x=6，即肉价是每两6文． 故答案为：6． 11.【答案】-16 ‎ ‎【解析】解：设∠AMB=θ，则∠AMC=π-θ．又=-，=-， ∴=（-）•（-）=•-•-•+， =-25-5×3cosθ-3×5cos（π-θ）+9=-16， 故答案为-16． 设∠AMB=θ，则∠AMC=π-θ，再由=（-）•（-）以及两个向量的数量积的定义求出结果． 本题主要考查两个向量的数量积的定义，属于基础题． 12.【答案】（0，） ‎ ‎【解析】解：由题意知，函数f（x）的定义域为（0，+∞）， 方程f′（x）=0在（0，+∞）有两个不同根； 即方程lnx-ax=0在（0，+∞‎ ‎）有两个不同根； 转化为函数y=lnx与函数y=ax的图象在（0，+∞）上有两个不同交点， 如右图． 可见，若令过原点且切于函数y=lnx图象的直线斜率为k， 只须0＜a＜k． 令切点A（x0，lnx0）， 故k=y′=，又k=， 故=， 解得，x0=e， 故k=， 故0＜a＜． 故答案为：（0，）． 由导数与极值的关系知可转化为方程f′（x）=lnx-ax=0在（0，+∞）有两个不同根；再转化为函数y=lnx与函数y=ax的图象在（0，+∞）上有两个不同交点，通过函数的导数利用曲线的斜率，从而求解a的范围； 本题考查了导数的综合应用，转化思想，数形结合的思想方法的应用，属于中档题． 13.【答案】5+2 ‎ ‎【解析】解：y=ln（x+b）的导数为y′=， 由切线的方程y=x-a可得切线的斜率为1， 可得切点的横坐标为1-b，切点为（1-b，0）， 代入y=x-a，得a+b=1， ∵a、b为正实数， 则+=（a+b）（+）=2+3++≥5+2=5+2． 当且仅当a=b，即a=，b=3-时，取得最小值5+2． 故答案为：5+2． 求函数的导数，由已知切线的方程，可得切线的斜率，求得切线的坐标，可得a+b=1，再由乘1法和基本不等式，即可得到所求最小值． 本题主要考查导数的应用，利用导数的几何意义以及基本不等式是解决本题的关键，属于中档题． 14.【答案】0 ‎ ‎【解析】h（x）=（x-3）lnx，h′（x）=lnx-+1， h″（x）=+＞0恒成立，∴h′（x）在（0，+∞）上单调递增， ∴存在x0，h′（x0）=0，即lnx0=-1， h（x）在（0，x0）上单调递减，（x0，+∞）上单调递增， ∴h（x）min=h（x0）=-（x0+）+6， ∵h′（）＜0，h′（2）＞0，∴x0∈（，2）， ∴h（x0）∈（-，-）， ∴存在λ的最小值0，使得关于x的不等式2λ≥h（x）有解； 故答案为：0 ‎ 令函数h（x）=（x-3）lnx，求出h（x）的最小值，根据函数的单调性判断即可； 本题考查导数知识的综合运用，考查函数的单调性与最值，考查分类讨论的数学思想，属于中档题． 15.【答案】解：（1）sin（α+）=， 即sinαcos+cosαsin=，化简：sinα+cosα=…① sin2α+cos2α=1…②． 由①②解得cosα=-或cosα= ∵α∈（，π）． ∴cosα=- （2）∵α∈（，π）．cosα=- ∴sinα=， 那么：cos2α=1-2sin2α=，sin2α=2sinαcosα= ∴sin（2α-）=sin2αcos-cos2αsin=． ‎ ‎【解析】（1）利用两角和差公式打开，根据同角三角函数关系式可求cosα的值； （2）根据二倍角公式求出cos2α，sin2α，利用两角和差公式打开，可得sin（2α-）的值． 本题主要考查了两角和差公式，同角三角函数关系式以及二倍角公式的运用和计算能力． 16.【答案】解：（I）在△ABC中，由•=求得cos‎2A=，可得． 再根据=cos＜，＞，求得cos＜，＞=， 可得向量与的夹角＜，＞=． （II）∵a=，A=，由余弦定理可得a2=5=b2+c2-2bc•cosA≥2bc-bc， 求得bc≤10+5，当且仅当b=c时取等号，故△ABC面积bc•sinA=的最大值为． ‎ ‎【解析】本题主要考查两个向量的数量积的定义，余弦定理以及基本不等式的应用，属于中档题． （I）在△ABC中，由•=求得cos‎2A=，可得A的值．再根据两个向量的数量积的定义求得向量与的夹角． （II）由条件利用余弦定理以及基本不等式求得bc的最大值，可得△ABC面积bc•sinA的最大值. 17.【答案】解：设包装盒的高为h（cm），底面边长为a（cm），则a=x，h=（30-x），0＜x＜30． （1）S=4ah=8x（30-x）=-8（x-15）2+1800， 答：当x=15时，S取最大值． （2）V=a2h=2（-x3+30x2），V′=6x（20-x）， 由V′=0得x=20， 当x∈（0，20）时，V′＞0；当x∈（20，30）时，V′＜0； 答：当x=20时，包装盒容积V（cm3‎ ‎）最大， 此时，． 即此时包装盒的高与底面边长的比值是． ‎ ‎【解析】（1）可设包装盒的高为h（cm），底面边长为a（cm），写出a，h与x的关系式，并注明x的取值范围．再利用侧面积公式表示出包装盒侧面积S关于x的函数解析式，最后求出何时它取得最大值即可； （2）利用体积公式表示出包装盒容积V关于x的函数解析式，最后利用导数知识求出何时它取得的最大值即可． 考查函数模型的选择与应用，考查函数、导数等基础知识，考查运算求解能力、空间想象能力、数学建模能力．属于基础题． 18.【答案】解：（1）由题意得：f（x）=log3（2-3x）， ∴2-3x＞0，即x＜， 所以函数f（x）的定义域为（-∞，）； （2）易知g（x）=loga（2-ax）-loga（2+ax）， ∵2-ax＞0且2+ax＞0， ∴关于原点对称， 又∵， ∴， ∴g（x）为奇函数． （3）令μ=2-ax， ∵a＞0，a≠1， ∴μ=2-ax在[2，3]上单调递减， 又∵函数f（x）在[2，3]递增， ∴0＜a＜1， ​又∵函数f（x）在[2，3]的最大值为1， ∴f（3）=1，即f（3）=loga（2‎-3a）=1， ∴， ∵0＜a＜1， ∴符合题意． 即存在实数，使函数f（x）在[2，3]递增，并且最大值为1． ‎ ‎【解析】本题考查了对数函数的性质，考查复合函数的单调性、最值问题，是一道中档题． （1）根据对数函数的性质求出函数的定义域即可； （2）根据函数奇偶性的定义判断即可； （3）令μ=2-ax，根据复合函数的单调性求出函数的最大值，从而求出对应的a的值即可． 19.【答案】解：（Ⅰ）∵a‎1a2a3…an=（n∈N*）①， 当n≥2，n∈N*时， ②， 由①②知：， 令n=3，则有． ‎ ‎∵b3=6+b2， ∴a3=8． ∵{an}为等比数列，且a1=2， ∴{an}的公比为q，则=4， 由题意知an＞0，∴q＞0，∴q=2． ∴（n∈N*）． 又由a‎1a2a3…an=（n∈N*）得： ， ， ∴bn=n（n+1）（n∈N*）． （Ⅱ）（i）∵cn===． ∴Sn=c1+c2+c3+…+cn = = = =； （ii）因为c1=0，c2＞0，c3＞0，c4＞0； 当n≥5时， ， 而 =＞0， 得 ， 所以，当n≥5时，cn＜0， 综上，对任意n∈N*恒有S4≥Sn，故k=4． ‎ ‎【解析】本题考查了等比数列通项公式、求和公式，还考查了分组求和法、裂项求和法和猜想证明的思想，证明可以用二项式定理，还可以用数学归纳法．本题计算量较大，思维层次高，要求学生有较高的分析问题解决问题的能力．本题属于难题． （Ⅰ）先利用前n项积与前（n-1）项积的关系，得到等比数列{an}的第三项的值，结合首项的值，求出通项an，然后现利用条件求出通项bn； （Ⅱ）（i）利用数列特征进行分组求和，一组用等比数列求和公式，另一组用裂项法求和，得出本小题结论；（ii）本小题可以采用猜想的方法，得到结论，再加以证明． 20.【答案】解：（Ⅰ）a=1时，y=（x2+x+1）ex，y′=（x+1）（x+2）ex， 令y′＞0，解得：x＞-1或x＜-2，令y′＜0，解得：-2＜x＜-1， ∴函数y=f（x）•g（x）在[-2，-1]递减，在[-1，0]递增， 而x=-2时，y=，x=0时，y=1， 故函数在[-2，0]上的最大值是1； （Ⅱ）由题意得：k==有且只有一个根， 令h（x）=，则h′（x）=， 故h（x）在（-∞，1）上单调递减，（1，2）上单调递增，（2，+∞‎ ‎）上单调递减， 所以h（x）极大=h（2）=，h（x）极小=h（1）=， 因为h（x）在（2，+∞）单调递减，且函数值恒为正，又当x→-∞时，h（x）→+∞， 所以当k＞或0＜k＜时，k=h（x）有且只有一个根． （Ⅲ）设x1＜x2，因为g（x）=ex在[0，2]单调递增， 故原不等式等价于|f（x1）-f（x2）|＜g（x2）-g（x1）在x1、x2∈[0，2]，且x1＜x2恒成立， 所以g（x1）-g（x2）＜f（x1）-f（x2）＜g（x2）-g（x1）在x1、x2∈[0，2]，且x1＜x2恒成立， 即，在x1、x2∈[0，2]，且x1＜x2恒成立， 则函数F（x）=g（x）-f（x）和G（x）=f（x）+g（x）都在[0，2]单调递增， 则有，在[0，2]恒成立， 当a≥-（ex+2x）恒成立时，因为-（ex+2x）在[0，2]单调递减， 所以-（ex+2x）的最大值为-1，所以a≥-1； 当a≤ex-2x恒成立时，因为ex-2x在[0，ln2]单调递减，在[ln2，2]单调递增， 所以ex-2x的最小值为2-2ln2，所以a≤2-2ln2， 综上：-1≤a≤2-2ln2． ‎ ‎【解析】（Ⅰ）求出函数的导数，得到函数的单调区间，从而求出函数的最大值即可； （Ⅱ）若a=-1，关于x的方程f（x）=k•g（x）有且仅有一个根，即k==，有且只有一个根，令h（x）=，可得h（x）极大=h（2）=，h（x）极小=h（1）=，进而可得当k＞或0＜k＜时，k=h（x）有且只有一个根； （Ⅲ）设x1＜x2，因为g（x）=ex在[0，2]单调递增，故原不等式等价于|f（x1）-f（x2）|＜g（x2）-g（x1）在x1、x2∈[0，2]，且x1＜x2恒成立，当a≥-（ex+2x）恒成立时，a≥-1；当a≤ex-2x恒成立时，a≤2-2ln2，综合讨论结果，可得实数a的取值范围． 本题考查的知识点是导数在最大值和最小值中的应用，利用导数分析函数的单调性，利用导数分析函数的极值，运算量大，综合性强，转化困难，属于难题． ‎