- 2021-04-15 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017中考真题圆
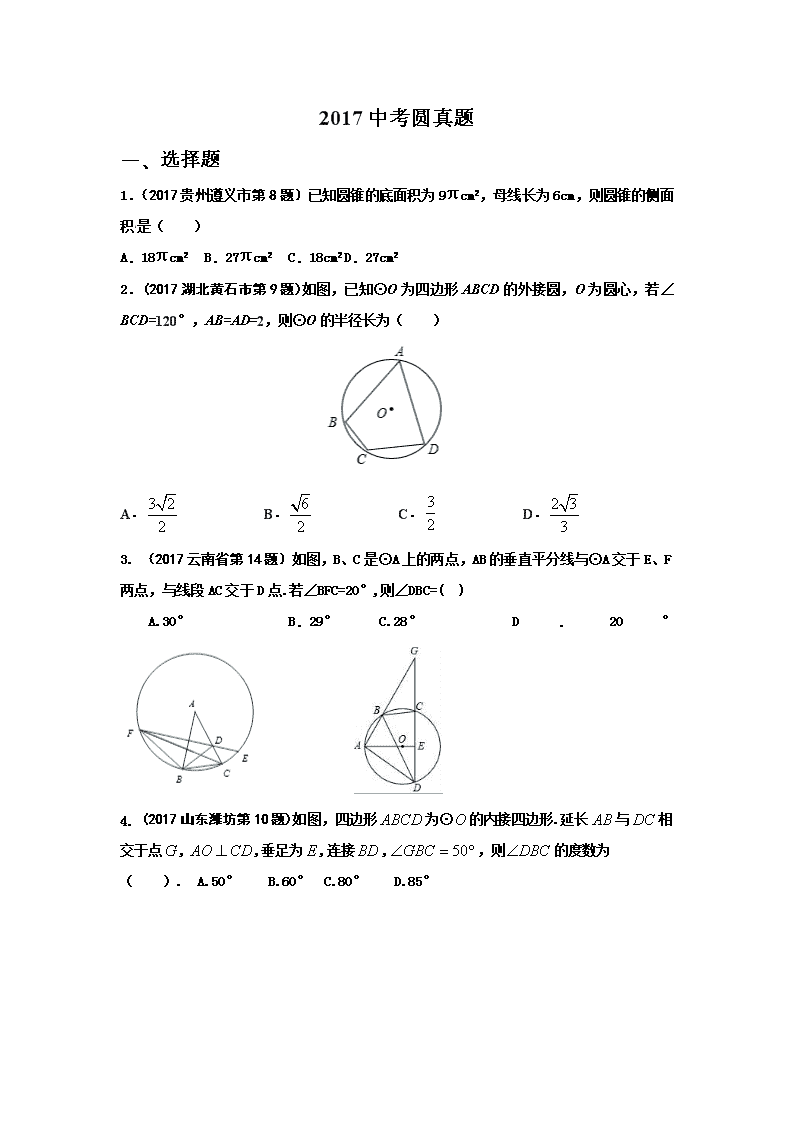
2017 中考圆真题 一、选择题 1.(2017 贵州遵义市第 8 题)已知圆锥的底面积为 9πcm2,母线长为 6cm,则圆锥的侧面 积 是( ) A.18πcm2 B.27πcm2 C.18cm2 D.27cm2 2.(2017 湖北黄石市第 9 题)如图,已知⊙O 为四边形 ABCD 的外接圆,O 为圆心,若∠ BCD=120°,AB=AD=2,则⊙O 的半径长为( ) A. B. C. D. 3. (2017 云南省第 14 题)如图,B、C 是⊙A 上的两点,AB 的垂直平分线与⊙A 交于 E、F 两点,与线段 AC 交于 D 点.若∠BFC=20°,则∠DBC=( ) A.30° B.29° C.28° D . 20 ° 4. (2017 山东潍坊第 10 题)如图,四边形 为⊙ 的内接四边形.延长 与 相 交于点 , ,垂足为 ,连接 , ,则 的度数为 ( ). A.50° B.60° C.80° D.85° 3 2 2 6 2 3 2 2 3 3 ABCD O AB DC G CDAO ⊥ E BD °=∠ 50GBC DBC∠ 5. (2017 山东潍坊第 12 题)点 为半径是 3 的圆周上两点,点 为 的中点,以线 段 、 为邻边作菱形 ,顶点 恰在该圆直径的三等分点上,则该菱形的边长为 ( ). A. 或 B. 或 C. 或 D. 或 6.(2017 内蒙古包头第 9 题)如图,在△ABC 中,AB=AC,∠ABC=45°,以 AB 为直径的 ⊙O 交 BC 于点 D,若 BC= ,则图中阴影部分的面积为( ) A.π+1 B.π+2 C.2π+2 D.4π+1 7.(2017 玉林崇左第 11 题)如图,大小不同的两个磁块,其截面都是等边三角形,小三角形 边长是大三角形边长的一半,点 是小三角形的内心,现将小三角形沿着大三角形的边缘 顺时针滚动,当由①位置滚动到④位置时,线段 绕点 顺时针转过的角度是( ) A. B. C. D. 8.(2017 玉林崇左第 12 题)如图, 是 的直径, 分别与 相交于点 ,连 接 ,现给出两个命题: ①若 ,则 ; ②若 ,记 的面积为 ,四边形 的面积为 ,则 ,那么( ) A.①是真命题,②是假命题 B.①是假命题,②是真命题 C.①是假命题,②是假命题 D.①是真命题,②是真命题 CA、 B AC BA BC ABCD D 5 22 5 32 6 22 6 32 4 2 O OA O 240° 360° 480° 540° AB O⊙ ,AC BC O⊙ ,D E DE AC AB= DE CE= 45C =∠ ° CDE△ 1S DABE 2S 1 2S S= 9.(2017 山东淄博市第 9 题)如图,半圆的直径 BC 恰与等腰直角三角形 ABC 的一条直角 边完全重合,若 BC=4,则图中阴影部分的面积是( ) A.2+π B.2+2π C.4+π D.2+4π 10.(2017 四川乐山市第 7 题)如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩, 他了解到这扇门的相关数据:这扇 圆弧形门所 在的圆与水平地面是相切的,AB=CD=0.25 米,BD=1.5 米,且 AB.CD 与水平地面都是垂直的.根据以上数据,请你帮小红计算出这 扇圆弧形门的最高点离地面的距离是( ) A.2 米 B.2.5 米 C.2.4 米 D.2.1 米 11.(2017 吉林第 6 题)如图,直线 l 是⊙O 的切线,A 为切点,B 为直线 l 上一点,连接 OB 交⊙O 于点 C.若 AB=12,OA=5,则 BC 的长为( ) A.5 B.6 C.7 D.8 12.(2017 湖南永州第 7 题)小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样 大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点 A,B,C,给出三 角形 ABC,则这块玻璃镜的圆心是( ) A.AB,AC 边上的中线的交点 B.AB,AC 边上的垂直平分线的交点 C.AB,AC 边上的高所在直线的交点 D.∠BAC 与∠ABC 的角平分线的交点 13.(2017 吉林长春市第 7 题)如图,点 A,B,C 在⊙O 上,∠ABC=29°,过点 C 作⊙O 的 切线交 OA 的延长线于点 D,则∠D 的大小为( ) A.29° B.32° C.42° D.58° 14.(2017 陕西省第 9 题)如图,△ABC 是⊙O 的内接三角形,∠C=30°,⊙O 的半径为 5,若点 P 是⊙O 上的一点,在△ABP 中,PB=AB,则 PA 的长为( )[来源:学+科+网 Z+X+X+K] A.5 B. C. D. 15.(2017 辽宁葫芦岛第 8 题)如图,点 A、B、C 是⊙O 上的点,∠AOB=70°,则∠ACB 的度数是( ) A.30° B.35° C.45° D.70° 5 3 2 5 2 5 3 16.(2017 江苏南通市第 6 题)如图,圆锥的底面半径为 2,母线长为 6,则侧面积为( ) A.4π B.6π C.12π D.16π 17.(2017 江苏南通市第 9 题)已知∠AOB,作图. 步骤 1:在 OB 上任取一点 M,以点 M 为圆心,MO 长为半径画半圆,分别交 OA、OB 于 点 P、Q; 步骤 2:过点 M 作 PQ 的垂线交 于点 C; 步骤 3:画射线 OC. 则下列判断:① = ;②MC∥OA;③OP=PQ;④OC 平分∠AOB,其中正确的个数 为( ) A.1 B.2 C.3 D.4 18.(2017云南省第13题)正如我们小学学过的圆锥体积公式 ( 表示圆周 率, 表示圆锥的地面半径, 表示圆锥的高)一样,许多几何量的计算都要用到 .祖冲之是 世界上第一个把 计算到小数点后 7 位的中国古代科学家,创造了当时世界上的最高水平, 差不多过了 1000 年,才有人把 计算得更精确.在辉煌成就的背后,我们来看看祖冲之付 出了多少.现在的研究表明,仅仅就计算来讲,他至少要对 9 位数字反复进行 130 次以上 的各种运算,包括开方在内.即使今天我们用纸笔来算,也绝不是一件轻松的事情,何况 那时候没有现在的纸笔,数学计算不是用现在的阿拉伯数字,而是用算筹(小竹棍或小竹 片)进行的,这需要怎样的细心和毅力啊!他这种严谨治学的态度,不怕复杂计算的毅力, 值得我们学习. 下面我们就来通过计算解决问题:已知圆锥的侧面展开图是个半圆,若该圆锥的体积等于 ,则这个圆锥的高等于( ) A. B. C. D. PQ PC CQ hrV 2 3 1π= π r h π π π π39 π35 35 π33 33 二、填空题 1.(2017 贵州遵义市第 17 题)如图,AB 是⊙O 的直径,AB=4,点 M 是 OA 的中点,过点 M 的直线与⊙O 交于 C,D 两点.若∠CMA=45°,则弦 CD 的长为 . 2.(2017 辽宁营口第 15 题)如图,将矩形 绕点 沿顺时针方向旋转 90°到矩形 的位置, ,则阴影部分的面积为 . 3.(2017 湖北恩施第 15 题)如图 5,在 中, ,以直角边 为直径作 半圆交 于点 ,以 为边作等边 ,延长 交 于点 , ,则图 中阴影部分的面积为 .(结果不取近似值) 4.(2017 内蒙古包头第 17 题)如图,点 A、B、C 为⊙O 上的三个点,∠BOC=2∠AOB,∠ BAC=40°,则∠ACB= 度. ABCD C A B C D′ ′ ′ ′ 2, 4AB AD= = Rt ABC△ 30BAC =∠ ° AB AC D AD ADE△ ED BC F 2 3BC = 5.(2017 浙江温州第13 题)已知扇形的面积为 ,圆心角为120°,则它的半径为________. 6.(2017 湖南永州第 16 题)如图,四边形 ABCD 是⊙O 的内接四边形,点 D 是的中点,点 E 是上的一点,若∠CED=40°,则∠ADC=________度. 7. (2017 湖南永州第 17 题)如图,这是某同学用纸板做成的一个底面直径为 10cm,高为 12cm 的无底圆锥形玩具(接缝忽略不计),则做这个玩具所需纸板的面积是_____________cm2(结 果保留 ).[来源:学科网 ZXXK] 8.(2017 湖北荆门市第 17 题)已知:如图, 内接于 ,且半径 ,点 在半径 的延长线上,且 ,则由 ,线段 和线段 所围成图形的阴影部分的面积为____________. 9.(2017 福建宁德市第 15 题)将边长为 2 的正六边形 ABCDEF 绕中心 O 顺时针旋转 α 度 与原图形重合,当 α 最小时,点 A 运动的路径长为 . 3π π ABC∆ O OC AB⊥ D OB 030 , 2A BCD AC∠ = ∠ = = BC CD BD 10.(2017 湖北鄂州市第 14 题)已知圆锥的高为 6,底面圆的直径为 8,则圆锥的侧面积 为 . 11.(2017 贵州贵阳市第 13 题)如图,正六边形 ABCDEF 内接于⊙O,⊙O 的半径为 6,则这个正六边形的边心距 OM 的长为 . 12.(2017 吉林长春市第 12 题)如图,则△ABC 中,∠BAC=100°,AB=AC=4,以点 B 为圆 心,BA 长为半径作圆弧,交 BC 于点 D,则 的长为 .(结果保留π) 13.(2017 江苏淮安市第 16 题)如图,在圆内接四边形 ABCD 中,若∠A,∠B,∠C 的度 数之比为 4:3:5,则∠D 的度数是 °. 14.(2017 江苏泰州市第 12 题)扇形的半径为 3cm,弧长为 2πcm,则该扇形的面积为 cm2. 15.(2017 江苏泰州市第 15 题)如图,在平面直角坐标系 xOy 中,点 A、B、P 的坐标分 别为(1,0),(2,5),(4,2).若点 C 在第一象限内,且横坐标、纵坐标均为整数,P 是 △ABC 的外心,则点 C 的坐标为 . 8 13π 16.(2017 湖北鄂州市第 14 题)已知圆锥的高为 6,底面圆的直径为 8,则圆锥的侧面积 为 . 17 .( 2017 江 苏 南 通 市 第 13 题 ) 四 边 形 ABCD 内 接 于 圆 , 若 ∠ A=110° , 则 ∠ C= 度. 18.(2017 云南省第 5 题)如图,边长为 4 的正方形 ABCD 外切于⊙O,切点分别为 E、F、 G、H.则图中阴影部分的面积为 . 19.(2017 吉林第 13 题)如图,分别以正五边形 ABCDE 的顶点 A,D 为圆心,以 AB 长为 半径画 , .若 AB=1,则阴影部分图形的周长为 (结果保留 π). 20.(2017 湖北黄石市第 13 题)如图,已知扇形 OAB 的圆心角为 60° ,扇形的面积为 6 π,则该扇形的弧长为 . BE CE 三、解答题 1.(2017 贵州遵义市 24 题)如图,PA、PB 是⊙O 的切线,A、B 为切点,∠APB=60°,连 接 PO 并延长与⊙O 交于 C 点,连接 AC,BC. (1)求证:四边形 ACBP 是菱形; (2)若⊙O 半径为 1,求菱形 ACBP 的面积. 2.(2017 辽宁营口第 23 题) 如图,点 在以 为直径的 上,点 是 的中点,过 点 作 垂直于 ,交 的延长线于点 ,连接 交 于点 . (1)求证: 是 的切线; (2)若 ,求 的长. E AB O C BE C CD AE AE D BE AC F CD O 4cos , 155CAD BF∠ = = AC 3.(2017 湖北黄石市第 21 题)如图,⊙O 是△ABC 的外接圆,BC 为⊙O 的直径,点 E 为 △ABC 的内心,连接 AE 并延长交 ⊙O 于 D 点,连接 BD 并延长至 F,使得 BD=DF,连接 CF、BE. (1)求证:DB=DE; (2)求证:直线 CF 为⊙O 的切线. 4. (2017 山东潍坊第 22 题)(本题满分 8 分)如图, 为半圆 的直径, 是⊙ 的 一条弦, 为 的中点,作 ,交 的延长线于点 ,连接 . (1)求证: 为半圆 的切线; (2)若 ,求阴影区域的面积.(结果保留根号和π) 5.(2017 湖北恩施第 23 题)如图, 、 是 的 直径, 是 的弦,且 , 过点 的切线与 的延长线交于点 ,连接 . (1)求证: 平分 ; (2)求证: ; (3)若 ,求 的半径. AB O AC O D BC ACDE ⊥ B F DA EF O 36== DFDA AB CD O⊙ BE O⊙ BE CD∥ C EB P BC BC ABP∠ 2PC PB PE= × 4BE BP PC- = = O⊙ 6.(2017 内蒙古包头第 24 题)如图,AB 是⊙O 的直径,弦 CD 与 AB 交于点 E,过点 B 的 切线 BP 与 CD 的延长线交于点 P,连接 OC,CB. (1)求证:AE•EB=CE•ED; (2)若⊙O 的半径为 3,OE=2BE, ,求 tan∠OBC 的值及 DP 的长. 7.(2017 浙江温州第 24 题)(本题 14 分)如图,已知线段 AB=2,MN⊥AB 于点 M,且 AM =BM,P 是射线 MN 上一动点,E,D 分别是 PA,PB 的中点,过点 A,M,D 的圆与 BP 的另一交点 C(点 C 在线段 BD 上),连结 AC,DE.[来源:学。科。网 Z。X。X。K] (1)当∠APB=28°时,求∠B 和 的度数; (2)求证:AC=AB。 (3)在点 P 的运动过程中 ①当 MP=4 时,取四边形 ACDE 一边的两端点和线段 MP 上一点 Q,若以这三点为顶 点的三角形是直角三角形,且 Q 为锐角顶点,求所有满足条件的 MQ 的值; ②记 AP 与圆的另一个交点为 F,将点 F 绕点 D 旋 转 90°得到点 G,当点 G 恰好落在 MN 上时,连结 AG,CG,DG,EG,直接写出△ACG 和△DEG 的 面积之比. CM 9 5 CE DE = 8.(2017 玉林崇左第 23 题)如图, 是 的直径, 是上半圆的弦,过点 作 的切 线 交 的延长线于点 ,过点 作切线 的垂线,垂足为 ,且与 交于点 , 设 , 的度数分别是 . (1)用含 的代数式表示 ,并直接写出 的取值范围; (2)连接 与 交于点 ,当点 是 的中点时,求 , 的值. 9.(2017 湖南益阳市第 20 题)(本小题满分 10 分)如图,AB 是⊙O 的直径,C 是⊙O 上一点,D 在 AB 的延长线上,且∠BCD=∠A. (1)求证:CD 是⊙O 的切线; (2)若⊙O 的半径为 3,CD=4,求 BD 的长. [来源:Zxxk.Com] N C E D M A B P AB O⊙ AC C O⊙ DE AB E A DE D O⊙ F DAC∠ CEA∠ ,a b a b a OF AC 'O 'O AC a b 10.(2017 山东淄博市第 23 题)如图,将矩形纸片 ABCD 沿直线 MN 折叠,顶点 B 恰好与 CD 边上的动点 P 重合(点 P 不与点 C,D 重合),折痕为 MN,点 M,N 分别在边 AD,BC 上,连接 MB,MP,BP,BP 与 MN 相交于点 F. (1)求证:△BFN∽△BCP; (2)①在图 2 中,作出经过 M,D,P 三点的⊙O(要求保留作图痕迹,不写做法); ②设 AB=4,随着点 P 在 CD 上的运动,若①中的⊙O 恰好与 BM,BC 同时相切,求此时 DP 的长. 11.(2017 四川乐山市第 24 题)如图,以 AB 边为直径的⊙O 经过点 P,C 是⊙O 上一点, 连结 PC 交 AB 于点 E,且∠ACP=60°,PA=PD. (1)试判断 PD 与⊙O 的位置关系,并说明理由; (2)若点 C 是弧 AB 的中点,已知 AB=4,求 CE•CP 的值. 12.(2017 湖南永州第 24 题)(本小题满分 10 分)如图,已知 AB 是⊙O 的直径,过 O 点作 OP ⊥AB,交弦 AC 于点 D,交⊙O 于点 E,且使∠PCA=∠ABC . (1)求证:PC 是⊙O 的切线; (2)若∠P=60°,PC=2,求 PE 的长. 13.(2017 湖北荆门市第 22 题)已知:如图,在 中, 的平分线 交 于点 ,过点 作 交 于点 ,以 为直径作 . (1)求证: 是 的切线; (2)若 ,求 的长. ABC∆ 090 ,C BAC∠ = ∠ AD BC D D DE AD⊥ AB E AE O BC O 3, 4AC BC= = BE 14.(2017 福建宁德市第 23 题)如图,BF 为⊙O 的直径,直线 AC 交⊙O 于 A,B 两点, 点 D 在⊙O 上,BD 平分∠OBC,DE⊥AC 于点 E. (1)求证:直线 DE 是⊙O 的切线; (2)若 BF=10,sin∠BDE= ,求 DE 的长. 15.(2017 湖北鄂州市第 22 题)(本题满分 9 分)如图,已知BF 是⊙O 的直径,A 为 ⊙O 上 (异于 B、F)一点. ⊙O 的切线 MA 与 FB 的延长线交于点 M;P 为 AM 上一点,PB 的延长线 交⊙O 于点 C,D 为 BC 上一点且 PA =PD,AD 的延长线交⊙O 于点 E.[来源:学科网 ZXXK] (1)求证: = ; (2)若 ED、EA 的长是一元二次方程 x2-5x+5=0 的两根,求 BE 的长; (3)若 MA =6 , , 求 AB 的长. BE CE 2 1sin 3AMF∠ = 16.(2017 贵州贵阳市第 22 题)如图,C、D 是半圆 O 上的三等分点,直径 AB=4,连接 AD、 AC,DE⊥AB,垂足为 E,DE 交 AC 于点 F. (1)求∠AFE 的度数; (3)求阴影部分的面积(结果保留π和根号). 17.(2017 陕西省第 23 题)如图,已知⊙O 的半径为 5,PA 是⊙O 的一条切线,切点为 A, 连接 PO 并延长,交⊙O 于点 B,过点 A 作 AC⊥PB 交⊙O 于点 C、交 PB 于点 D,连接 BC,当∠P=30°时. (1)求弦 AC 的长; (2)求证:BC∥PA. 18.(2017 辽宁葫芦岛第 24 题)如图,△ABC 内接于⊙O,AC 是直径,BC=BA,在∠ACB 的内部作∠ACF=30°,且 CF=CA,过点 F 作 FH⊥AC 于点 H,连接 BF. (1)若 CF 交⊙O 于点 G,⊙O 的半径是 4,求 的长; (2)请判断直线 BF 与⊙O 的位置关系,并说明理由. 19.(2017 江苏淮安市第 25 题)如图,在△ABC 中,∠ACB=90°,O 是边 AC 上一点,以 O 为圆心,OA 为半径的圆分别交 AB,AC 于点 E,D,在 BC 的延长线上取点 F,使得 BF=EF, EF 与 AC 交于点 G. (1)试判断直线 EF 与⊙O 的位置关系,并说明理由; (2)若 OA=2,∠A=30°,求图中阴影部分的面积. 20.(2017 江苏泰州市第 24 题)如图,⊙O 的直径 AB=12cm,C 为 AB 延长线上一点,CP 与⊙O 相切于点 P,过点 B 作弦 BD∥CP,连接 PD. (1)求证:点 P 为 的中点; (2)若∠C=∠D,求四边形 BCPD 的面积. 21.(2017 湖北鄂州市第 22 题)如图,已知 BF 是⊙O 的直径,A 为⊙O 上(异于 B、F) 一点,⊙O 的切线 MA 与 FB 的延长线交于点 M;P 为 AM 上一点,PB 的延长线交⊙O 于 BD 点 C,D 为 BC 上一点且 PA=PD,AD 的延长线交⊙O 于点 E. (1)求证: ; (2)若 ED、EA 的长是一元二次方程 x2﹣5x+5=0 的两根,求 BE 的长; (3)若 MA=6 ,sin∠AMF= ,求 AB 的长. 22.(2017 江苏南通市第 24 题)如图,Rt△ABC 中,∠ C=90°,BC=3,点 O 在 AB 上, OB=2,以 OB 为半径的⊙O 与 AC 相切于点 D,交 BC 于点 E,求弦 BE 的长. BE CE= 2 1 3查看更多