- 2021-04-15 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
七年级下册数学教案8-4 三元一次方程组的解法 2 人教版
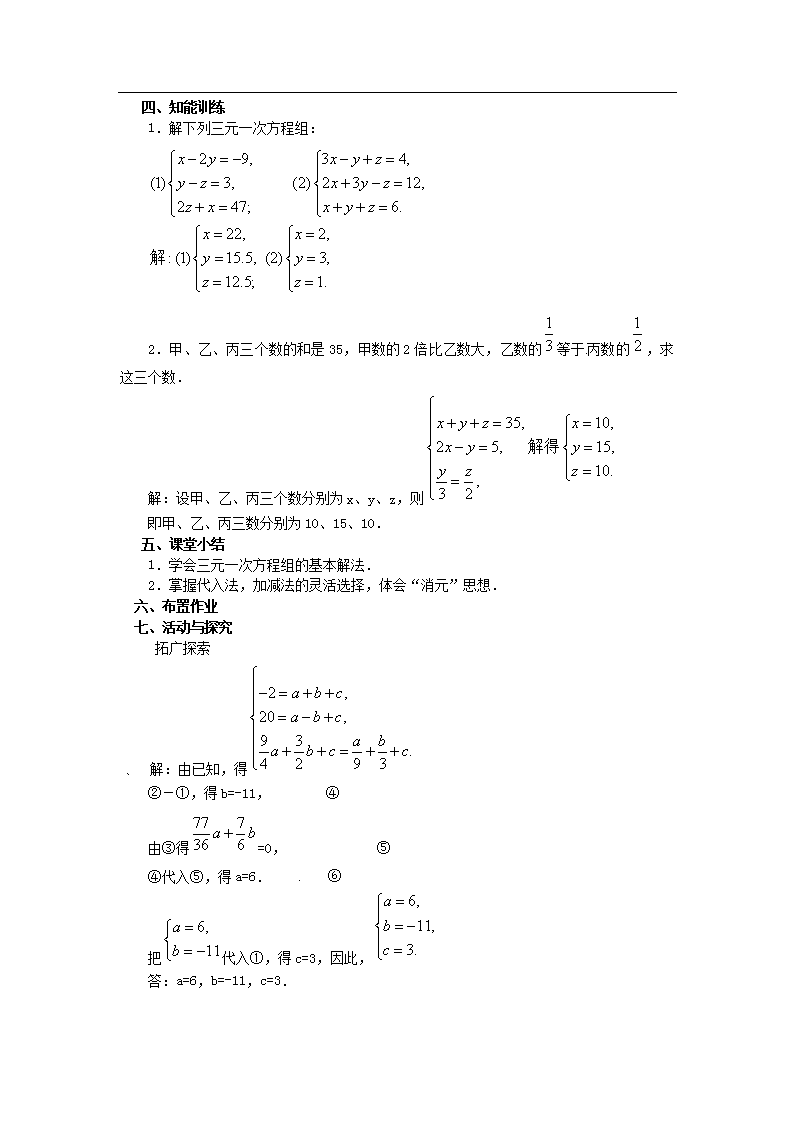
*8.4 三元一次方程组的解法 【教学目标】 1.理解三元一次方程组的含义. 2.会解某个方程只有两元的简单的三元一次方程组. 3.掌握解三元一次方程组过程中化三元为二元或一元的思路. 【教学重点与难点】 1.使学生会解简单的三元一次方程组. 2.通过本节学习,进一步体会“消元”的基本思想. 3. 针对方程组的特点,灵活使用代入法、加减法等重要方法. 【教学过程】 一、导入新课 前面我们学习了二元一次方程组的解法.有些问题,可以设出两个未知数,列出二元一次方程组来求解.实际上,有不少问题中含有更多的未知数.大家看下面的问题. 二、推进新课[来源:学科网ZXXK] 出示引入问题 小明手头有12张面额分别为1元,2元,5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍,求1元,2元,5元纸币各多少张. 1.题目中有几个未知数,你如何去设? 2.根据题意你能找到等量关系吗? 3.根据等量关系你能列出方程组吗? 请大家分组讨论上述问题.[来源:学科网ZXXK] (教师对学生进行巡回指导) 学生成果展示: 1.设1元,2元,5元各x张,y张,z张.(共三个未知数) 2.三种纸币共12张;三种纸币共22元;1元纸币的数量是2元纸币的4倍. 3.上述三种条件都要满足,因此可得方程组 师:这个方程组有三个相同的未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组. 怎样解这个方程组呢?能不能类比二元一次方程组的解法,设法消去一个或两个未知数,把它化成二元一次方程组或一元一次方程呢? (学生小组交流,探索如何消元.) 可以把③分别代入①②,便消去了x,只包含y和z二元了: 解此二元一次方程组得出y、z,进而代回原方程组可求x.[来源:学科网ZXXK] 教师对学生的想法给予肯定并总结解三元一次方程组的基本思路:通过“代入”或“加减”进行消元,把“三元”化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而转化为解一元一次方程. 即三元一次方程组 二元一次方程组 一元一次方程 三、例题讲解 例1:解三元一次方程组 (让学生独立分析、解题,方法不唯一,可分别让学生板演后比较.) 解:②×3+③,得11x+10z=35. ①与④组成方程组 把x=5,z=-2代入②,得y=. 因此,三元一次方程组的解为 归纳:此方程组的特点是①不含y,而②③中y的系数为整数倍关系,因此用加减法从②③中消去y后,再与①组成关于x和z的二元一次方程组的解法最合理.反之用代入法运算较烦琐. 例2:在等式y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60,求a,b,c的值. (师生一起分析,列出方程组后交由学生求解.) 解:由题意,得三元一次方程组 ②-①,得a+b=1, ④ ③-①,得4a+b=10. ⑤[来源:Z,xx,k.Com] ④与⑤组成二元一次方程组. 解得 把a=3,b=-2代入①,得c=-5. 因此, 答:a=3,b=-2,c=-5. 四、知能训练 1.解下列三元一次方程组: 2.甲、乙、丙三个数的和是35,甲数的2倍比乙数大,乙数的等于丙数的,求这三个数. 解:设甲、乙、丙三个数分别为x、y、z,则 即甲、乙、丙三数分别为10、15、10. 五、课堂小结 1.学会三元一次方程组的基本解法. 2.掌握代入法,加减法的灵活选择,体会“消元”思想. 六、布置作业 七、活动与探究 拓广探索[来源:Z#xx#k.Com] 解:由已知,得 ②-①,得b=-11, ④ 由③得=0, ⑤ ④代入⑤,得a=6. ⑥ 把代入①,得c=3,因此, 答:a=6,b=-11,c=3.查看更多