- 2021-04-15 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2018届一轮复习人教A版2-2玩转一题学透三角小题大做学案
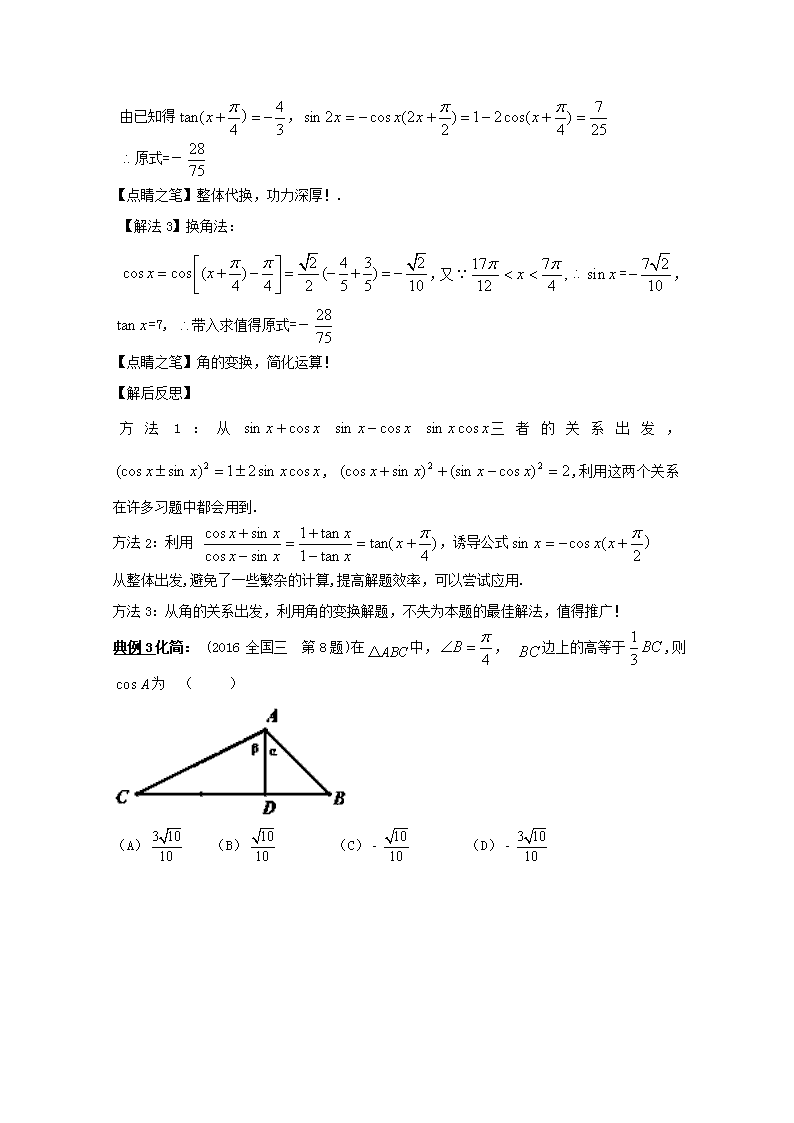
专题2.2 玩转一题学透三角 一、典例分析,融合贯通 典例1 中,,则= 【解法1】基本公式法: ,解得或(舍) 【点睛之笔】解题莫忘“本” 【解法2】平方法 (1) ,平方得:,可以看成是方程的两根, 中,, 【点睛之笔】三角函数平方显神威! 【点睛之笔】平方后别忘开方,判定符号是关键! 【解法4】齐次式法:由解法2得, 解得或, 【点睛之笔】.齐次式,弦化切 【解法5】观察法: 由勾三股四弦五可观察的的正余弦和有关, 中,猜得 【点睛之笔】小题小做,提速神器. 【解后反思】解法1:基本公式是解题的根源,往往容易被忽略! 解法2:是常用公式,恰当运用可以起到事半功倍的效果! 解法3:由结合法2可得=2! 解法4:齐次式可以把正余弦化为正切,是解决正切问题的利器! 解法5:充分利用填空题的特点,小题小做,提高解题速度! 本题五种解法包括了三角公式基本变换常用的几种方法和特值法,题目简单,但方法多元化,把难题解简单,把简单题解精彩是解题的一种境界,与其跳进题海不能自拔,不如仔细研究这样一题收获丰厚. 典例2已知 【点睛之笔】化简求值,逐个击破! 【解法2】整体代换法: =, 由已知得, 原式=- 【点睛之笔】整体代换,功力深厚!. 【解法3】换角法: ,又=,=7, 带入求值得原式=- 【点睛之笔】角的变换,简化运算! 【解后反思】 方法1:从三者的关系出发,, ,利用这两个关系在许多习题中都会用到. 方法2:利用 ,诱导公式 从整体出发,避免了一些繁杂的计算,提高解题效率,可以尝试应用. 方法3:从角的关系出发,利用角的变换解题,不失为本题的最佳解法,值得推广! 典例3化简: (2016 全国三 第8题)在中,, 边上的高等于,则为 ( ) (A) (B) (C) (D) 【点睛之笔】两角和正切求角! 【解法2】(三角函数法2) 如图, 【点睛之笔】. 两角和余弦求角! 【解法3】余弦定理法: 设则,利用余弦定理 【点睛之笔】巧设变量求余弦! 【解法4】正弦定理法: 设则 ,明显为钝角, 【点睛之笔】巧设变量求正弦! 【点睛之笔】巧用面积求角度!. 【解法6】面积法: 取中点,, 设则 利用余弦定理求出 【点睛之笔】角度转化求正弦! 【解后反思】解法1和解法2:从不同的角度用了两角和的正切和余弦求值,角度不同方法统一: 解法3和解法4利用了利用余弦和正弦来求解,是解决此类问题的通法! 解法5:以面积为中间纽带,求出角度的正弦! 解法6:利用平面几何知识转化求角,简化了运算,值得尝试! 二、精选试题,能力升级 1、已知,则等于 ( ) A. B. C. D. 【答案】C 【解析】,故选C. 2、已知,且,则的值为( ) A. B. C. D. 【答案】C 3、若 ,则( ) (A) (B) (C) 1 (D) 【答案】A 【解析】由,得或,所以,故选A. 4、已知,则的值是( ) A. B. C. D. 【答案】C 【解析】将 展开,合并同类项有,所以 ,故,选C. 5、已知非零实数满足关系式,则的值是( ) A. B. C. D. 【答案】C 6、已知, ,则( ) A. B. C. D. 【答案】D 【解析】由题意可得,即,则,所以,即,也即,所以,应选答案D。 7、已知,则( ) A. B. C. D. 【答案】B 8、过点,且倾斜角为的直线与圆相交于两点,若,则的值为 (A) (B) (C) (D) 【答案】D 9、已知,则( ) A. B. C. D. 【答案】C 【解析】因为,所以 ,可得 ,故选C. 10.【2015高考重庆,理9】若,则( ) A、1 B、2 C、3 D、4 【答案】C查看更多