高中数学选修2-2教学课件6_1_1归纳推理

高中数学选修2-2教学课件6_1_1归纳推理

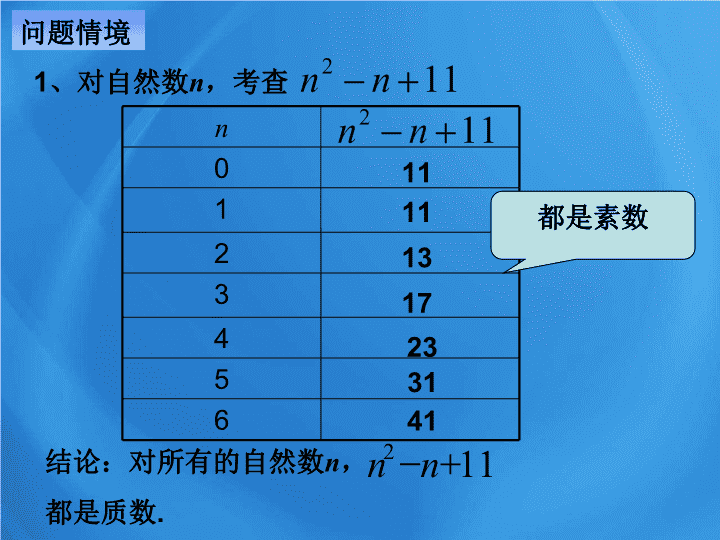
推理与证明 推理 证明 直接证明 间接证明 言之有理，论证有据！ 演绎推理 合情推理 第三章 推理与证明 问题情境 1 、对自然数 n ，考查 n 0 1 2 3 4 5 6 11 11 13 31 17 23 41 都是素数 结论： 对所有的自然数 n ， 都是质数 . 11 2 + - n n 2 、 前提 ：矩形的对角线的平方等于其长和宽的平方和 . 结论 ：长方体的对角线的平方等于其长、宽、高的平 方和 . 3 、 前提 ：所有的树都是植物， 梧桐是树 . 问题 1 是 归纳推理 ； 问题 2 是 类比推理 ； 问题 3 是 演绎推理 ； 结论 ：梧桐是植物 . 已知的判断 新的判断 确定 根据一个或几个已知的判断来确定一个新的判断的思维过程就叫 推理 . 6.1.1 归 纳 推 理 著名 猜想 　 哥德巴赫 ，德国数学家。 1742 年 6 月 7 日，他在 写给著名数学家欧拉 的一封信中，提出了 两个大胆的猜想： 1 、任何不小于 6 的偶数， 都是两个奇质数之和： 2 、任何不小于 9 的奇数， 都是 3 个奇质数之和 . 这就是数学史上 著名的 “ 哥德巴赫猜想 ” . 3 ＋ 7 ＝ 10 3 ＋ 17 ＝ 20 13 ＋ 17 ＝ 30 10 ＝ 3 ＋ 7 20 ＝ 3 ＋ 17 30 ＝ 13 ＋ 17 6 ＝ 3+3 ， 8 ＝ 3+5, 10 ＝ 5+5, …… 1000 ＝ 29+971 ， 1002=139+863, …… 猜想任何一个不小于 6 的偶数都等于两个奇质数的和 . 数学皇冠上璀璨的明珠 —— 哥德巴赫猜想 一个规律： 偶数＝奇质数＋奇质数 归纳推理 哥德巴赫猜想 (Goldbach Conjecture) 世界近代三大数学难题之一 1742 年，哥德巴赫在教学中发现，每个不小于 6 的偶数都是两个素数（只能被 1 和它本身整除的数）之和。如 6 ＝ 3 ＋ 3 ， 12 ＝ 5 ＋ 7 等等。 猜想 ( a ) 任何一个≥ 6 之偶数，都可以表示成两个奇质数之和。    ( b ) 任何一个≥ 9 之奇数，都可以表示成三个奇质数之和。 有人对 33×108 以内且大过 6 之偶数一一进行验算，哥德巴赫猜想 ( a ) 都成立。 目前最佳的结果是中国数学家陈景润于 1966 年证明的，称为陈氏定理 (Chen‘s Theorem).“ 任何充份大的偶数都是一个质数与一个自然数之和，而后者仅仅是两个质数的乘积” , 通常都简称这个结果为大偶数可表示为 “ 1+2” 的形式。 1920 年，挪威的布朗证明了“ 9+9” 。    1924 年，德国的拉特马赫证明了“ 7 + 7” 。    1932 年，英国的埃斯特曼证明了“ 6 + 6” 。 　　 ……… 　　　 ……… 200 年过去了，没有人证明它。哥德巴赫猜想由此成为数学皇冠上一颗可望不可及的“明珠”。到了 20 世纪 20 年代，才有人开始向它靠近。 陈氏定理 (Chen‘s Theorem) 任何充分大的偶数都是一个质数与一个自然数之和，而后者仅仅是两个质数的乘积 , 简称为 “ 1 + 2 ” 。 哥德巴赫猜想的过程： 具体的材料 观察分析 猜想出一般性的结论 归纳推理的过程： 由某类事物的 具有某些特征 , 推出该类事物的 都具有这些特征 的推理 , 或者由 概括出 的推理 , 称为 归纳推理 ( 简称归纳 ). 部分对象 全部对象 个别事实 一般结论 归纳推理 例 1 蛇是用肺呼吸的 , 鳄鱼是用肺呼吸的， 海龟也是用肺呼吸的， 蜥蜴是用肺呼吸的， 蛇 、 鳄鱼 、 海龟 、 蜥蜴都是爬行动物 . 例 2 三角形的内角和是 , 凸四边形的内角和是 , 凸五边形的内角和是 … 例题解析： 由此我们猜想 : 凸边形的内角和是 . 所以，所有的爬行动物都是用肺呼吸的 . 特殊 一般 例 3 、由下图可以发现什么结论？ 1+3=4=2 2 ， 1+3+5=9=3 2 ， 1+3+5+7=16=4 2 ， …… 由此猜想 : 前 n 个连续的奇数的和 等于 n 的平方 , 即 1+3+5+…+(2 n -1)= n 2 例 4 已知数列 { a n } 的第 1 项 a 1 =1 ，且 （ n =1 , 2 , …), 试归纳出这个数列的通项公式 . 解：分别把 n=1,2,3,4 代入 得 归纳 : 解法 2 取倒数得 例 5 在印度北部的佛教圣地贝拿勒斯的圣庙里有三根木桩，其中一根木桩上套有 64 个金属做的圆盘 , 圆盘的尺寸由上到下一个比一个大，这就是所谓“梵塔” . 现在有一位高僧正在把这些圆盘在三根木桩上移来移去 , 一次只能够移一个，而且不管什么时候，较大的圆盘都必须放在较小的圆盘的下面 , 当他把 64 个圆盘从原来的木桩上移到另一根木桩上的时候，就是“世界末日”到了 , 那一天，宇宙将在一声巨大的霹雳声中毁灭，梵塔、宇宙、高僧以及芸芸众生都将同归于尽 . 有三根针和套在一根针上的若干金属片 . 按下列规则 , 把金属片从一根针上全部移到另一根针上 . 1. 每次只能移动一个金属片 ; 2. 较大的金属片不能放在较小的金属片上面 . 试推测 : 把 n 个金属片从 1 号针移到 3 号针 , 最少需要移动多少次 ? n =1 时 , n =2 时 , n =1 时 , n =3 时 , n =2 时 , n =1 时 , n =2 时 , n =1 时 , n =3 时 , n =4 时 , n =3 时 , n =2 时 , n =1 时 , n =4 时 , n =3 时 , n =2 时 , n =1 时 , 归纳 : 1 、通项公式的归纳 2 、递推公式的归纳 按 1 秒钟搬动一次，而且整年整月都不停息， 1 年可搬： 所以，搬运的时间大约需要： 例 6(2005 年广东 ) 设平面内有 n 条直线 ( n ≥3), 其中有且仅有两条直线互相平行 , 任意三条直线不过同一点 . 若用 f ( n ) 表示这 n 条直线交点的个数 , f (4)= , 当 n >4 时 , f ( n )= .( 用 n 表示 ) 累加得 : f( n )=f( n -1)+ n -1 例 7 : 数一数图中的凸多面体的面数 F 、顶点数 V 和棱数 E , 然后用归纳法推理得出它们之间的关系 . 多面体 面数 ( F ) 顶点数 ( V ) 棱数 ( E ) 三棱锥 四棱锥 三棱柱 五棱锥 立方体 正八面体 五棱柱 截角正方体 尖顶塔 4 6 4 5 5 6 5 9 8 多面体 面数 ( F ) 顶点数 ( V ) 棱数 ( E ) 三棱锥 四棱锥 三棱柱 五棱锥 立方体 正八面体 五棱柱 截角正方体 尖顶塔 4 6 4 5 5 6 5 9 8 6 6 8 6 12 8 12 6 10 多面体 面数 ( F ) 顶点数 ( V ) 棱数 ( E ) 三棱锥 四棱锥 三棱柱 五棱锥 立方体 正八面体 五棱柱 截角正方体 尖顶塔 4 6 4 5 5 6 5 9 8 6 6 8 6 12 8 12 6 10 7 7 9 16 9 10 15 10 15 F + V - E =2 猜想 欧拉公式 例 8 、观察下列式子，归纳结论： （以下 a 、 b 均为正数） 练习 如右图三角阵 , 从上往下数 , 第 1 次全行的数都为 1 的是第 1 行 , 第 2 次全行的数为 1 的是第 3 行 , … , 第 n 次全行的数都为 1 的是第 行 ; 第 61 行中 1 的个数是 . 第 1 行 1 1 第 2 行 1 0 1 第 3 行 1 1 1 1 第 4 行 1 0 0 0 1 第 5 行 1 1 0 0 1 1 … … 已知 ， 请根据式 子提出猜想。 思考 四色猜想 四色原理 四色猜想的提出来自英国。 1852 年，毕业于伦敦大学的弗南西斯 · 格来到一家单位搞地图着色工作时，发现了一种有趣的现象：“ 每幅地图都可以用四种颜色着色，使得有共同边界的国家着上不同的颜色。 ”这个结论能不能从数学上加以严格证明呢？他和在大学读书的弟弟格里斯决心试一试。兄弟二人为证明这一问题而使用的稿纸已经堆了一大叠，可是研究工作没有进展。 电子计算机问世以后，加快了对四色猜想证明的进程。 1976 年，美国数学家阿佩尔与哈肯在两台不同的电子计算机上，用了 1200 个小时，作了 100 亿判断，终于完成了四色定理的证明 。四色猜想的计算机证明，轰动了世界 , 当时中国科学家也在研究这个原理。 它不仅解决了一个历时 100 多年的难题，而且有可能成为数学史上一系列新思维的起点。 任何形如 的数都是质数这就是著名的 " 费马猜想 " 观察到都是质数 , 进而 猜想 : 费马猜想 欧拉 半个世纪后 , 宣布了费马的这个猜想不成立 , 它不能作为一个求质数的公式 . 以后 , 人们又陆续发现 不是质数 . 至今这样的反例共找到了 46 个 , 却还没有找到第 6 个正面的例子 , 也就是说目前只有 n=0,1,2,3,4 这 5 个情况下 ,Fn 才是质数 . 大胆猜想 小心求证 天文学上的博德定律 行星名 博德推算的与太阳的距离 实际距离 水星 4 3.9 金星 7 7.2 地球 10 10.0 火星 16 15.2 28 木星 52 52.0 土星 100 95.3 单位： 1/10 天文单位（ AV ） 1766 年 1781 年天王星： 192 （ 196 ） 1801 年第一颗最大的小行星： 27.6 （ 28 ） 1930 年冥王星： 396 （ 388 ） 应用归纳推理可以发现新事实，获得新结论 3 ， 6 ， 12 ， 24 ， 48 ， 96 ， (*) 这个数列 (*) ，就是一个满足 an+1=2an 的数列。 如果对数列 (3) 的每一项都加上 4 ，便得到表中博德推算的距离： 　 4 ， 7 ， 10 ， 16 ， 28 ， 52 ， 100 ， … (4) 哥尼斯堡七桥问题 18 世纪在哥尼斯堡城的普莱格尔河上有 7 座桥，将河中的两个岛和河岸连结， 城中的居民经常沿河过桥散步，于是提出了一个问题： 能否一次走遍 7 座桥，而每座桥只许通过一次， 最后仍回到起始地点 。这就是七桥问题，一个著名的图 论问题。 欧拉 归纳推理的基础 归纳推理的作用 归纳推理 观察、分析 发现新事实、获得新结论 由部分到整体、 个别到一般的推理 注意 归纳推理的结论不一定成立 归纳推理的一般步骤： 试验、观察 概括、推广 猜测一般性结论 小结 2. 归纳推理的一般步骤 : (1) 通过观察个别情况发现某些相同性质 ; (2) 从已知的相同性质中推出一个明确表达的一般性命题 ( 猜想 ). 1. 什么是归纳推理 （简称 归纳 ） ? 部分　 → 　整体 个别 → 一般 成语 “ 一叶知秋 ” 意思是从一片树叶的凋落，知道秋 天将要来到 . 比喻由 细微的迹象 看出 整体 形势 的变化，由 部分 推知 全体 . 总结： 归纳推理 牛顿发现万有引力 门捷列夫发现元素周期律 应用归纳推理可以 发现新事实 , 获得新结论 ! 归纳推理是科学发现的重要途径 ! 歌德巴赫猜想 四色定理