小学数学人教版五年级上册第六七单元《多边形的面积和植树问题》复习课件

小学数学人教版五年级上册第六七单元《多边形的面积和植树问题》复习课件

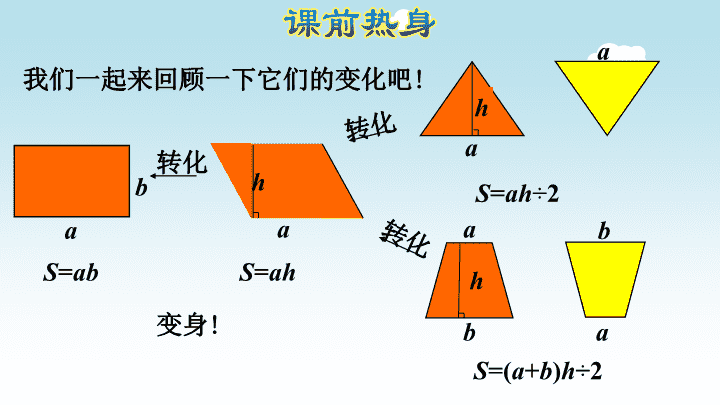
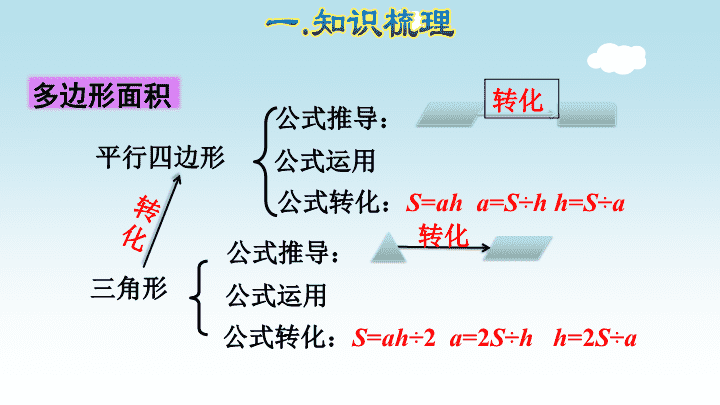
多边形的面积 数学广角—植树问题 RJ 五年级上册 我们一起来回顾一下它们的变化吧! 变身! a a a b a b h h a h S=ah S=ah÷2 S=(a+b)h÷2 转化 转化 转化a S=ab b 多边形面积 公式推导： 公式运用 公式转化：S=ah a=S÷h h=S÷a 平行四边形 三角形 公式推导： 公式运用 公式转化：S=ah÷2 a=2S÷h h=2S÷a 转 化 转化 转化 多边形面积 公式推导： 公式运用 公式转化：S=ah a=S÷h h=S÷a 平行四边形 梯形 公式推导： 公式运用 公式转化：S=(a+b)h÷2 h=2S÷(a+b) (a+b)=2S÷h 转 化 转化 转化 多边形面积 公式推导： 公式运用 公式转化：S=ah a=S÷h h=S÷a 平行四边形 组合图形： 转化 要有转化、切补思想 平行四边形转 化成长方形 1、平行四边形 1.平行四边形的底越长，它的面积就越大。( ) 底 底 小试牛刀 2.两个( )的三角形可以拼成一个平行四边形． A．面积相等 B．形状相同 C．等底等高 D．完全一样 C 2.2×9=19.8(m2) 3.计算面积 思想：三角形转 化成平行四边形 两个完全一 样的三角形 2、三角形 1.面积相等的两个三角形，形状也一定相同。 ( ) ∟ 3 3 4 4 小试牛刀 2.三角形的面积等于平行四边形面积的一半。( ) 3.一个三角形的底扩大2倍，高不变，它的面积也 会扩大2倍。 ( ) 4.等底等高的两个三角形，形状不一定相同，但它 们的面积一定相等。 ( ) 5.求直角三角形的面积 5 4 3 ∟ 2 .4 ①3×4÷2 ②3×5÷2 ③4×5÷2 ④5×2.4÷2 ⑤3×2.4÷2 ⑥4×2.4÷2 哪些算式正确？( )①④ 6.一个三角形，面积20平方米，高10米，底是 ( )米。 A．200 B．2 C．4 7.一个三角形，高不变，底扩大3倍，面积就 扩大( )倍。 A .3 B.6 C.9 C a=2S÷h A 7×8÷2=28(m2) 8.计算面积 9.一个三角形的底是15厘米，如果底缩小3厘米，面 积就缩小18平方厘米。原来三角形的面积是( ) 平方厘米。 15厘米 3厘米 18平方厘米 18×2÷3=12(cm) (15+3)×12÷2=108(cm2) 108 两个完全一 样的梯形 思想：梯形转化 成平行四边形 3、梯形 2.两个面积相等的梯形，形状也一定相同。( ) 1.面积相等的两个梯形一定能拼成一个平行四边形。 ( )3 5 4 3 5 4∟ 小试牛刀 (3+5)×3÷2=12(m2) 3.计算面积 4.一堆钢管，最高层12根，最下层23根，从上 到下每层(最上层除外)比上一层多1根，共堆 了12层，这样的两堆钢管一共有多少根？ (12+23)×12÷2×2=420(根) 答：这样的两堆钢管一共有420根。 求面积。 S=ah S=ah÷2 S=(a+b)h÷2 图形 平行四边形 三角形 梯形 底/ cm 7.5 6 10.2 24 上 4.2 下 6.7 上8 下12 高/ cm 3.12 4.3 5.8 12.5 4 15 面积 / cm2 23.4 25.8 29.58 150 21.8 150 图形 底 高 面积 平行四边形 4m ① 12㎡ 三角形 ② 8dm 24 d㎡ h=S÷a h=2S÷a 3m 6dm 平方千米 公顷 平方米 平方分米 平方厘米 100 10000 100 1001000000 面积单位的进率 350 cm2＝(　　)dm22.9 m2＝(　　　　)dm2290 3.5 单位换算：大化小用乘法，乘以他们之间的 进率，小化大用除法，除以他们之间的进率。 0.07公顷＝(　　)m2 700 1200 cm2＝(　　　)m20.12 小试牛刀 6公顷=( )平方米 700平方千米=( )公顷 80公顷=( )平方米=( )平方千米 一块黑板的面积大约是400( ) 校园占地面积大约是2( ) 安徽省的面积大约是14万( ) 平方厘米 公顷 平方千米 60000 70000 800000 0.8 1.多边形面积的应用 分的方法1 长方形加上梯形 长方形的面积＝6×5＝30(cm2) 梯形的面积＝(5＋10)×(12－6)÷2 ＝15×6÷2 ＝45(cm2) 组合图形的面积＝30＋45＝ 75(cm2) 分的方法2 三角形加上梯形 三角形的面积＝10×(12－6)÷2 ＝10×6÷2 ＝30(cm2) 梯形的面积＝(6＋12)×5÷2 ＝18×5÷2 ＝45(cm2) 组合图形的面积＝30＋45＝75(cm2) 2m 一、求阴影部分的面积. 2×2+4×4－4×6÷2 =8+16－12 =12(m2) 二、下图是教室的一面墙。如果 砌这面墙每平方米用砖185 块，一共需要多少块砖？ 这面墙的面积＝三角形的面积＋ 长方形的面积 二、下图是教室的一面墙。如果 砌这面墙每平方米用砖185 块，一共需要多少块砖？ 185×(5×4+5×1.2÷2)=4255(块) 三、实验小学有一块劳动基地，如图，A地种白菜，B地 种萝卜，C地种辣椒。 (1)如果种辣椒的面积是20 m2，那么种萝卜的面积是多少 平方米？ 高：20×2÷5=8(平方米) 萝卜的面积：8×6=48(平方米) 三、实验小学有一块劳动基地，如图，A地种白菜，B地 种萝卜，C地种辣椒。 (2)如果每平方米能收白菜27千克，那么A地能收白菜多少 千克？ A面积：(3+9)×8÷2=48(平方米) 白菜：27×48=1296(平方米) 四、一个平行四边形和一个梯形的高都是8 cm，梯形 的下底与平行四边形的底重合，都是25 cm，梯形 的上底比下底少3 cm，梯形的面积比平行四边形 的面积少多少平方厘米？ 解:25×8－(25＋25－3)×8÷2=12(平方厘米) 答:梯形的面积比平行四边形的面积少12平方厘米. 解析： 根据题意,可用25减去3计算出梯形上底的长度,然后 再利用梯形的面积=(上底+下底)高计算出梯形的面积,用 平行四边形的面积=底高计算出平行四边形的面积,最后 再用平行四边形的面积减去梯形的面积即可。 此题主要考查的是梯形面积公式和平行四边形面积 公式的灵活应用。 (1)两端都种： 棵数=间隔数+1 (2)两端不种： 棵数 = 间隔数－1 植树问题 植树问题 (4)封闭图形: 棵树 = 间隔数 (3)一端种 一端不种: 棵数 = 间隔数 一、五年级学生排成一个正方形的体操队形，最外层每 边12人。最外层一共有多少人？这个体操队形里一 共有学生多少人？ 解:12×4－4 =48－4 =42(人) 12×12=144(人) 答:最外层一共42人,这 个体操队形里一共 有144名同学. 解析：最外层人数=每边人数;实心方阵中总人数=每 边人数每边人数;代入数据即可解答。 二、在一个人工湖的周围每隔6米栽一棵柳树，一共栽了 150棵。再在相邻的两颗柳树之间每隔2米栽一棵杨 树，一共栽了多少棵杨树？ 解：6÷2－1=2(棵) 150×2=300(棵) 答：一共栽了300棵樱花。 答案详解：本题考查学生是否掌握植树问题 的解答方法，以及根据不同的情况选择合适 的方法；在封闭路线上栽树，树的棵数=间隔 数；在两头都不栽时，树的棵数=间隔数－1.