- 2021-04-14 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2010年广西河池市中考数学试卷
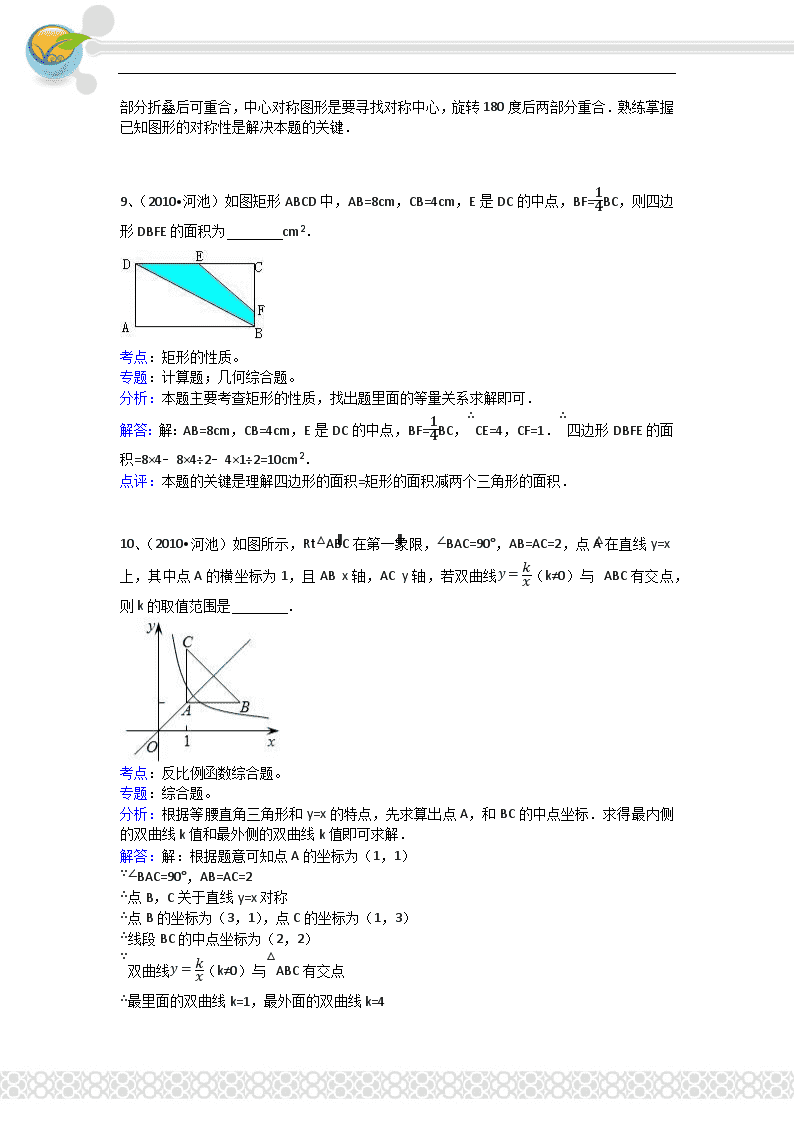
一、填空题(共10小题,每小题2分,满分20分) 1、(2010•钦州)计算:|﹣2010|= . 考点:绝对值。 分析:负数的绝对值是它本身的相反数. 解答:解:|﹣2010|=2010. 点评:主要考查了绝对值的运算,先确定绝对值符号中数的正负,再去绝对值符号. 2、(2010•河池)如图,在▱ABCD中,∠A=120°,则∠D= 度. 考点:平行四边形的性质。 专题:计算题。 分析:利用平行四边形的性质得两边平行,两邻角互补,从而求出∠D的度数. 解答:解:平行四边形中两组对边分别平行则AB∥CD, 根据两直线平行同旁内角互补∠A+∠D=180°, 当∠A=120°时,∠D=60° 故答案为60. 点评:此题主要考查了平行四边形的性质,平行四边形的对角相等,邻角互补. 3、(2010•河池)要使分式2xx﹣3有意义,则x须满足的条件为 . 考点:分式有意义的条件。 专题:计算题。 分析:要使分式有意义,分式的分母不能为0. 解答:解:因为分式2xx﹣3有意义,所以x﹣3≠0,即x≠3. 点评:解此类问题,只要令分式中分母不等于0,求得x的值即可. 4、(2010•河池)分解因式:9﹣a2= . 考点:因式分解-运用公式法。 分析:有两项,都能写成完全平方数的形式,并且符号相反,可用平方差公式展开. 解答:解:9﹣a2, =32﹣a2, =(3+a)(3﹣a). 点评:本题考查了利用平方差公式分解因式,熟记公式结构是解题的关键. 5、(2010•河池)在一个不透明的口袋中装有若干个只有颜色不同的球,如果已知袋中只有3个红球,且一次摸出一个球是红球的概率为13,那么袋中的球共有 个. 考点:概率公式。 分析:利用红球的概率公式列出方程求解即可. 解答:解:设袋中共有x个球,根据概率公式得: 3x=13, x=9. 答:袋中的球共有9个. 点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=mn. 6、(2010•永州)方程x2﹣x=0的解是 . 考点:解一元二次方程-因式分解法。 专题:计算题。 分析:本题应对方程进行变形,提取公因式x,将原式化为两式相乘的形式,再根据“两式相乘值为0,这两式中至少有一式值为0”来解题. 解答:解:原方程变形为:x(x﹣1)=0, ∴x=0或x=1. 点评:本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的提点灵活选用合适的方法.本题运用的是因式分解法. 7、(2010•通化)现有甲、乙两支排球队,每支球队队员身高的平均数均为1.85米,方差分别为S甲2=0.32,S乙2=0.26,则身高较整齐的球队是 队. 考点:方差;算术平均数。 分析:根据方差的意义解答. 解答:解:∵s甲2>s乙2, ∴身高较整齐的球队是乙队. 故填乙. 点评:本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为x,则方差S2=1n[(x1﹣x)2+(x2﹣x)2+…+(xn﹣x)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立. 8、(2010•河池)写出一个既有轴对称性质又有中心对称性质的图形名称: . 考点:中心对称图形;轴对称图形。 专题:开放型。 分析:根据轴对称图形与中心对称图形的概念,在所学过的图形中寻找. 解答:解:如线段、圆、正方形、矩形、菱形、正2n边形(n为正整数)等.答案不唯一. 点评: 掌握好中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.熟练掌握已知图形的对称性是解决本题的关键. 9、(2010•河池)如图矩形ABCD中,AB=8cm,CB=4cm,E是DC的中点,BF=14BC,则四边形DBFE的面积为 cm2. 考点:矩形的性质。 专题:计算题;几何综合题。 分析:本题主要考查矩形的性质,找出题里面的等量关系求解即可. 解答:解:AB=8cm,CB=4cm,E是DC的中点,BF=14BC,∴CE=4,CF=1.∴四边形DBFE的面积=8×4﹣8×4÷2﹣4×1÷2=10cm2. 点评:本题的关键是理解四边形的面积=矩形的面积减两个三角形的面积. 10、(2010•河池)如图所示,Rt△ABC在第一象限,∠BAC=90°,AB=AC=2,点A在直线y=x上,其中点A的横坐标为1,且AB∥x轴,AC∥y轴,若双曲线y=kx(k≠0)与△ABC有交点,则k的取值范围是 . 考点:反比例函数综合题。 专题:综合题。 分析:根据等腰直角三角形和y=x的特点,先求算出点A,和BC的中点坐标.求得最内侧的双曲线k值和最外侧的双曲线k值即可求解. 解答:解:根据题意可知点A的坐标为(1,1) ∵∠BAC=90°,AB=AC=2 ∴点B,C关于直线y=x对称 ∴点B的坐标为(3,1),点C的坐标为(1,3) ∴线段BC的中点坐标为(2,2) ∵双曲线y=kx(k≠0)与△ABC有交点 ∴最里面的双曲线k=1,最外面的双曲线k=4 即1≤k≤4. 故答案为:1≤k≤4. 点评:此题综合考查了反比例函数与一次函数的性质,此题难度稍大,综合性比较强,注意对各个知识点的灵活应用,求得双曲线k值. 二、选择题(共8小题,每小题3分,满分24分) 11、(2010•河池)下列各数中,最小的实数是( ) A、﹣5 B、3 C、0 D、2 考点:实数大小比较。 分析:由于正数都大于0,负数都小于0,由此即可判定最小的数. 解答:解:因为正数都大于0,负数都小于0,所以一切负数小于一切正数. A、﹣5<0,比0小; B、3>0,比负数大; C、0=0,比负数大; D、2>0,比负数大. 综上所述,﹣5最小. 故选A. 点评:此题主要考查了实数的大小的比较,实数大小比较法则:正数大于0,0大于负数,正数大于负数. 12、(2010•河池)下列说法中,完全正确的是( ) A、打开电视机,正在转播足球比赛 B、抛掷一枚均匀的硬币,正面一定朝上 C、三条任意长的线段都可以组成一个三角形 D、从1,2,3,4,5这五个数字中任取一个数,取到奇数的可能性较大 考点:可能性的大小;三角形三边关系;随机事件。 分析:根据随机事件的定义,可能性的求法,三角形三边关系得到正确选项即可. 解答:解:A、B、C、可能发生,也可能不发生,是随机事件,不一定正确,不符合题意; D、正确,从1,2,3,4,5这五个数字中任取一个数,取到奇数的可能性为35. 故选D. 点评:用到的知识点为:不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件; 两条可能性等于所求情况数与总情况数之比. 较小的线段之和大于最大的线段的三条线段组成三角形. 13、(2010•河池)如图所示,图中几何体的主视图为( ) A、 B、 C、 D、 考点:简单组合体的三视图。 分析:找到从正面看所得到的图形即可. 解答:解:从正面看可得到下面是一个长方形,上面是一个圆,圆在长方形上中间的位置,故选C. 点评:本题考查了三视图的知识,主视图是从物体的正面看得到的视图. 14、(2010•河池)下列运算正确的是( ) A、a2﹣a3=a6 B、(a2)3=a5 C、3a+2a=5a D、a6÷a3=a2 考点:同底数幂的除法;合并同类项;幂的乘方与积的乘方。 分析:根据同底数幂的乘法与除法、合并同类项、幂的乘方的运算法则计算即可. 解答:解:A、a2、a3不是同类项,不能合并,故本选项错误; B、应为(a2)3=a2×3=a6,故本选项错误; C、3a+2a=(3+2)a=5a,正确; D、应为a6÷a3=a6﹣3=a2,故本选项错误. 故选C. 点评:本题考查合并同类项、同底数幂的除法、幂的乘方,熟练掌握性质是解题的关键,合并同类项时只把系数相加减,字母与字母的次数不变,不是同类项的一定不能合并. 15、(2010•河池)计算8﹣2的结果是( ) A、6 B、6 C、2 D、2 考点:二次根式的加减法。 分析:根据二次根式加减的一般步骤,先化简,再合并. 解答:解:8﹣2=22﹣2 =2,故选D. 点评:同类二次根式是指几个二次根式化简成最简二次根式后,被开方数相同的二次根式. 二次根式的加减运算,先化为最简二次根式,再将被开方数相同的二次根式进行合并. 合并同类二次根式的实质是合并同类二次根式的系数,根指数与被开方数不变. 16、(2010•河池)在Rt△ABC中,∠C=90°,AC=12,BC=5,将△ABC绕边AC 所在直线旋转一周得到圆锥,则该圆锥的侧面积是( ) A、25π B、65π C、90π D、130π 考点:圆锥的计算;勾股定理。 专题:操作型。 分析:运用公式s=πlr(其中勾股定理求解得到得母线长l为13)求解. 解答:解:由已知得,母线长l=13,半径r为5, ∴圆锥的侧面积是s=πlr=13×5×π=65π. 故选B. 点评:要学会灵活的运用公式求解. 17、(2010•河池)化简:(a2a﹣3+93﹣a)÷a+3a的结果是( ) A、﹣a B、a C、(a+3)2a D、1 考点:分式的混合运算。 分析:先计算括号里的,再把除法转化成乘法计算. 解答:解:(a2a﹣3+93﹣a)÷a+3a=a2﹣9a﹣3•aa+3=a. 故选B. 点评:对于一般的分式混合运算来讲,其运算顺序与整式混合运算一样,是先乘方,再乘除,最后算加减,如果遇括号要先算括号里面的. 18、(2010•河池)如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的是( ) A、①② B、①②③ C、①②④ D、①②③④ 考点:勾股定理。 分析:大正方形的面积是49,则其边长是7,显然,利用勾股定理可得①x2+y2=49; 小正方形的面积是4,则其边长是2,根据图可发现y+2=x,即②x﹣y=2; 还可以得出四个三角形的面积+小正方形的面积=大正方形的面积,即4×12xy+4=49,化简得 ③2xy+4=49; 其中④x+y=9无法证明,故不成立. 解答:解:①大正方形的面积是49,则其边长是7,显然,利用勾股定理可得x2+y2=49,故选项①正确; ②小正方形的面积是4,则其边长是2,根据图可发现y+2=x,即x﹣y=2,故选项②正确; ③根据图形可得四个三角形的面积+小正方形的面积=大正方形的面积,即4×12xy+4=49,化简得2xy+4=49,故选项③正确; ④x+y=9,无法证明,故此选项不正确. 故选B. 点评:本题利用了勾股定理、面积分割法等知识. 三、解答题(共8小题,满分76分) 19、(2010•河池)计算:∣﹣31∣+(1+2)0﹣+(﹣2)2﹣sin60° 考点:实数的运算。 分析:计算时,先去绝对值,开平方,把三角函数化成实数后再计算即可求解. 解答:解:原式=32+1+4﹣32 =5. 点评:此题主要考查了实数的运算.其中无理数的运算法则与有理数的运算法则是一样的.在进行根式的运算时要先化简再计算可使计算简便. 20、(2010•河池)如图所示,点B和点C分别为∠MAN两边上的点,AB=AC. (1)按下列语句画出图形: ①AD⊥BC,垂足为D; ②∠BCN的平分线CE与AD的延长线交于点E; ③连接BE. (2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形: ≌ , ≌ ;并选择其中的一对全等三角形,予以证明. 考点:全等三角形的判定。 专题:作图题。 分析:(1)①从A作AD⊥BC,垂足为D,D在线段BC上; ②作∠BCN的平分线CE与AD的延长线交于点E,E在线段AD的延长线上; ③连接BE就是过B、E两点画线段; (2)还有△ABE≌△ACE;△BDE≌△CDE.其中证明△ABE≌△ACE的条件有AB=AC、∠BAE=∠CAE、AE公共,由此即可证明;证明△BDE≌△CDE的全等条件有&BD=CD&∠BDE=∠CDE=90°&DE=DE,由此即可证明结论. 解答:解:(1)①②③,如图所示: (2)△ABE≌△ACE,△BDE≌△CDE. (3)选择△ABE≌△ACE进行证明. ∵AB=AC,AD⊥BC, ∴∠BAE=∠CAE, 在△ABE和△ACE中&AB=AC&∠BAE=∠CAE&AE=AE ∴△ABE≌△ACE(SAS); 选择△BDE≌△CDE进行证明. ∵AB=AC,AD⊥BC, ∴BD=CD, 在△BDE和△CDE中&BD=CD&∠BDE=∠CDE=90°&DE=DE, ∴△BDE≌△CDE(SAS) . 点评:本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目. 21、(2010•河池)如图所示,在平面直角坐标系中,梯形ABCD的顶点坐标分别为:A(2,﹣2),B(3,﹣2),C(5,0),D(1,0),将梯形ABCD绕点D逆时针旋转90°得到梯形A1B1C1D. (1)在平面直角坐标系中画出梯形A1B1C1D, 则A1的坐标为 , B1的坐标为 , C1的坐标为 ; (2)点C旋转到点C1的路线长为 (结果保留π) 考点:弧长的计算;作图-旋转变换。 分析:(1)将梯形ABC三点绕点D逆时针旋转90°,得到新的坐标,顺次连接得到梯形A1B1C1D.并从图上读出点的坐标. (2)点C旋转到点C1的路线长是一段弧长,根据弧长的公式计算. 解答:解:(1) 画梯形A1B1C1D就是所画的图形.(2分) A1的坐标为(3,1), B1的坐标为(3,2), C1的坐标为(1,4); (2)点C旋转到点C1的路线长=90π×4180=2π. 点评:本题主要考查了旋转变换作图及从坐标系中读出点的坐标的方法,及弧长公式的计算方法. 22、(2010•河池)河池市近年来大力发展旅游业,吸引了众多外地游客前来观光旅游,某旅行社对2009年“十•一”国庆期间接待的外地游客作了抽样调查.河池的首选旅游线路(五大黄金旅游线路)的调查结果如下图表:(如图所示) (1)此次共抽样调查了 人; (2)请将以上图表补充完整; (3)该旅行社预计五大黄金旅游线路今年“十•一”国庆期间接待外地游客约20 000人,请你估计外地游客首选三姐故乡游的人数约有 人. 考点:频数(率)分布表;用样本估计总体;条形统计图。 专题:图表型。 分析:(1)用90÷0.30即可求出抽样调查的人数; (2)首先根据总人数和表格的已知数据求出民俗风情游的人数,然后根据表格的数据即可补全统计图; (3)由于知道外地游客首选三姐故乡游的人数的频率,利用样本估计总体的思想可以求出外地游客首选三姐故乡游的人数. 解答:解:(1)∵90÷0.30=300, ∴共抽样调查了900人; (2)图表补充如图所示:; (3)依题意得20000×0.25=5000人, ∴外地游客首选三姐故乡游的人数为5000人. 点评:本题难度中等,考查统计图表的识别;解本题要懂得频率分布直分图的意义,了解频率分布直分图是一种以频数为纵向指标的条形统计图. 23、(2010•河池)李明骑自行车去上学途中,经过先上坡后下坡的一条路段,在这段路上所走的路程S(米)与时间t(分钟)之间的函数关系如图所示.根据图象,解答下列问题: (1)求李明上坡时所走的路程S1(米)与时间t(分钟)之间的函数关系式和下坡时所走的路程S2(米)与时间t(分钟)之间的函数关系式; (2)若李明放学后按原路返回,且往返过程中,上坡的速度相同,下坡的速度也相同,问李明返回时走这段路所用的时间为多少分钟. 考点:一次函数的应用。 专题:应用题。 分析:(1)分别设s1=k1t(0≤t≤6),s2=k2t+b(6<t≤10),根据图象的已知点的坐标利用待定系数法可求得函数关系式; (2)分别求出上坡时间与下坡时间相加即可,注意上坡和下坡的路程和速度要根据图象计算. 解答:解:(1)设s1=k1t(0≤t≤6) ∵图象经过点(6,900) ∴900=6k1 解方程,得 k1=150 ∴s1=150t(0≤t≤6) 设s2=k2t+b(6<t≤10) ∵图象经过点(6,900),(10,2100) ∴&6k2+b=900&10k2+b=2100 解这个方程组,得 &k2=300&b=﹣900 ∴s2=300t﹣900(6<t≤10) (2)李明返回时所用时间为 (2100﹣900)÷(900÷6)+900÷[(2100﹣900)÷(10﹣6)]=8+3=11(分钟) 答:李明返回时所用时间为11分钟. 点评:主要考查了根据实际问题列函数关系式的能力和读图能力.准确的解读函数图象得到需要的信息是解题的关键.还要会熟练的运用待定系数法求函数关系式. 24、(2010•河池)去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件. (1)求饮用水和蔬菜各有多少件? (2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来; (3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360 元.运输部门应选择哪种方案可使运费最少?最少运费是多少元? 考点:一元一次不等式组的应用;二元一次方程组的应用。 专题:方案型。 分析:(1)关系式为:饮用水件数+蔬菜件数=320; (2)关系式为:40×甲货车辆数+20×乙货车辆数≥200;10×甲货车辆数+20×乙货车辆数≥120; (3)分别计算出相应方案,比较即可. 解答:解:(1)设饮用水有x件,则蔬菜有(x﹣80). x+(x﹣80)=320 解这个方程,得x=200,x﹣80=120 答:饮用水和蔬菜分别为200件和120件; (2)设租用甲种货车m,则租用乙种货车(8﹣m). 得: &40m+20(8﹣m)≥200&10m+20(8﹣m)≥120, 解这个不等式组,得2≤m≤4 (. m整数,∴m=2或3或4,安排甲、乙两种货车时有3种方案. 设计方案分别为: ①甲车2辆,乙车6辆;②甲车3辆,乙车5辆;③甲车4辆,乙车4辆; (3)3种方案的运费分别为: ①2×400+6×360=2960元;②3×400+5×360=3000元;③4×400+4×360=3040元. ∴方案①运费最少,最少运费是2960元. 答:运输部门应选择甲车2辆,乙车6辆,可使运费最少,最少运费是2960元. 点评:解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的关系式. 25、(2010•河池)如图所示,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H. (1)如果⊙O的半径为4,CD=43,求∠BAC的度数; (2)若点E为ADB的中点,连接OE,CE.求证:CE平分∠OCD; (3)在(1)的条件下,圆周上到直线AC距离为3的点有多少个?并说明理由. 考点:垂径定理;等腰三角形的性质;圆心角、弧、弦的关系;平行线分线段成比例。 专题:几何综合题。 分析:(1)先求出CH的长,利用三角形的角边关系求出角BOC,然后就可求出∠COH. (2)利用等腰三角形的性质得出∠E=∠OCE,再利用平行线的判定得出OE∥CD即可证明CE 平分∠OCD; (3)点到直线的距离的定义得出.做垂直于AC的线段且距离为3,从该线段的另一段作AC的平行线,与圆的交点,即是圆周上到直线AC距离为3的点,这样的点有2个. 解答:解:(1)∵AB为⊙O的直径,CD⊥AB ∴CH=12CD=23(1分) 在Rt△COH中,sin∠COH=CHOC=32 ∴∠COH=60° (2分) ∵OA=OC ∴∠BAC=12∠COH=30°;(3分) (2)∵点E是ADB的中点 ∴OE⊥AB (4分) ∴OE∥CD ∴∠ECD=∠OEC (5分) 又∵∠OEC=∠OCE ∴∠OCE=∠DCE (6分) ∴CE平分∠OCD;(6分) (3)圆周上到直线AC的距离为3的点有2个. (8分) 因为圆弧AC上的点到直线AC的最大距离为2,ADC上的点到直线AC的最大距离为6,2<3<6,根据圆的轴 对称性,ADC到直线AC距离为3的点有2个. (10分) 点评:本题综合考查了圆心角,弧弦的关系,学生在做这一部分题时,一定要把圆的有关知识综合使用. 26、(2010•河池)如图所示,在直角梯形OABC,CB,OA,∠OAB=90°,点O为坐标原点,点A在x半轴上,对角线OB,AC相交于点M,OA=AB=4,OA=2CB. (1)线段OB的长为 ,点C的坐标为 ; (2)求△OCM的面积; (3)求过O,A,C三点的抛物线的解析式; (4)若点E在(3)的抛物线的对称轴上,点F为该抛物线上的点,且以A,O,F,E四点为顶点的四边形为平行四边形,求点F的坐标. 考点:二次函数综合题。 专题:压轴题。 分析:(1)易证得△OAB是等腰Rt△,已知了直角边的长,即可根据直角三角形的性质求出斜边OB的长;已知了OA=2BC,即可得到C点的横坐标,而B、C的纵坐标相同,由此可求出C点的坐标; (2)易证得△BCM∽△OAM,且OA=2BC,根据相似三角形的对应边成比例可得AM=2CM;由此可证得△OAM的面积是△OCM的2倍,即△OCM的面积是△OAC的13,因此只需求出△OAC的面积即可; (3)用待定系数法即可求出经过O、A、C三点的函数解析式; (4)根据(3)得到的抛物线的解析式,即可求出其对称轴方程;若以A,O,F,E四点为顶点的四边形为平行四边形,应分成两种情况考虑: ①E点在x轴的下方,F在x轴的上方;此时四边形OFAE的对角线OA、EF互相平分,四边形OFAE是平行四边形,此时F与C点重合; ②E、F同时在x轴下方;此时四边形OAFE(或OAEF)以OA为边,根据平行四边形的对边互相平行且相等知:OA=EF,由此可求出F点的横坐标,将其代入抛物线的解析式中,即可求得F点的坐标. 解答:解:(1)在Rt△OAB中,OA=AB=4,所以△AOB是等腰Rt△, OB=2OA=42,B(4,4); ∵OA=2BC,则C点位于OA的垂直平分线上, ∴C(2,4); (2)在直角梯形OABC中,OA=AB=4,∠OAB=90°, ∵CB∥OA, ∴△OAM∽△BCM,(3分) 又∵OA=2BC, ∴AM=2CM,CM=13AC,(4分) 所以S△OCM=13S△OAC=13×12×4×4=83;(5分) (注:另有其它解法同样可得结果,正确得本小题满分.) (3)设抛物线的解析式为y=ax2+bx+c(a≠0), 由抛物线的图象经过点O(0,0),A(4,0),C(2,4), 所以&c=0&16a+4b+c=0&4a+2b+c=4,(6分) 解这个方程组得a=﹣1,b=4,c=0,(7分) 所以抛物线的解析式为: y=﹣x2+4x;(8分) (4)∵抛物线y=﹣x2+4x的对称轴是CD,x=2, ①当点E在x轴的下方时,CE和OA互相平分则可知四边形OEAC为平行四边形,此时点F和点C重合, 点F的坐标即为点C(2,4);(9分) ②当点E在x轴的下方,点F在对称轴x=2的右侧,存在平行四边形AOEF,OA∥EF,且OA=EF, 此时点F的横坐标为6, 将x=6代入y=﹣x2+4x,可得y=﹣12. 所以D(6,﹣12). (11分) 同理,点F在对称轴x=2的左侧,存在平行四边形OAEF,OA∥FE,且OA=FE, 此时点F的横坐标为﹣2, 将x=﹣2代入y=﹣x2+4x,可得y=﹣12, 所以F(﹣2,﹣12). (12分) 综上所述,点F的坐标为(2,4),(6,﹣12),(﹣2,﹣12).(12分) 点评:此题主要考查了解直角三角形、三角形面积的求法、二次函数解析式的确定以及平行四边形的判定等知识,同时还考查了分类讨论的数学思想,综合性强,难度偏大. 参与本试卷答题和审题的老师有: 张伟东;CJX;Linaliu;lanyuemeng;huangling;zhehe;cook2360;zhangchao;MMCH;lanchong;nhx600;haoyujun;lanyan;fuaisu;路斐斐;lzhzkkxx;wangcen;mama258;kaixinyike;wdxwwzy;yu123;littlenine;智波;算术。(排名不分先后) 2011年2月17日查看更多